多种任务调度混合的IB-LBM并行优化方法

刘智翔，刘慧超，黄冬梅，2*，周丽萍，苏 诚

（1.上海海洋大学信息学院，上海201306；2.上海电力大学，上海200090；3.上海大学计算机工程与科学学院，上海200444；4.国家海洋局东海分局东海预报中心，上海200136）

0 引言

格子玻尔兹曼法（Lattice Boltzmann Method，LBM）是一种介于微观和宏观尺度上模拟流体运动的方法。LBM的流场演化过程清晰，在处理具有多种流体成分或者具有复杂边界的流场时更具有优势；但当流场中包含有复杂的几何结构物体时，流场和浸入边界的结合处往往会涉及到繁琐的网格生成以及复杂的流场求解过程，造成模型的计算复杂性上升，降低了执行效率。

为了简化流场中浸入边界的计算，Peskin［1］提出了浸入边界法（Immersed Boundary Method，IBM）。即用固定的欧拉网格表示流场，将浸入的边界看作具有高刚度系数且可以发生形变的边界，用拉格朗日点（Lagrangian Point）表示。当边界发生形变，会产生一种恢复力，将边界恢复到原来形状。将边界上的力分布到流场中，最后求解整个流场，这就是IBM的基本思想。基于IBM 和LBM 通常应用于欧拉网格这一个共同点，可以将两种方法进行结合。Feng 等［2］首次成功应用浸入边界-格子玻尔兹曼方法（Immersed Boundary-Lattice Boltzmann Method，IB-LBM）来模拟刚体粒子的运动。其后经过不断的突破和发展，IB-LBM 已成为研究流固耦合问题的热门方法。在研究细胞形变方面，Ma 等［3］将IB-LBM 引入超声效应的影响，模拟红细胞（Red Blood Cell，RBC）在超声场中的聚集和形变，研究了红细胞的瞬态聚集行为以及形变的详细过程；对于流体与弹性物体的耦合问题，Afra 等［4］提出了一种基于IB-LBM与鲁棒格子弹簧模型（Lattice Spring Model，LSM）相结合的流体与弹性体相互作用模型，研究了稳定流态、旋涡脱落流态和刚体运动极限等不同的流动条件，并提出了一种计算弹性体变形的通用公式；Gong 等［5］将非线性有限元方法（Finite Element Method，FEM）引入到IB-LBM 框架，研究非可压缩流体中移动的可变形物体的非线性流固耦合问题；在模拟多孔介质流动问题上，Wang 等［6］将IB-LBM 应用于多孔壳体的液体俘获和形变，以模拟浆环反应器中由多孔壳体包围刚性固芯组成的膨胀聚乙烯（PolyEthylene，PE）颗粒在流体中的复杂流动行为。

在使用IB-LBM 求解流场时，为了得出比较精确的结果，往往需要规模较大、较密集的流场网格，这就会造成模拟过程时间长的问题。IB-LBM 模拟流场时，计算恢复力、体积力离散，计算平衡分布函数、碰撞和迁移，计算宏观量，都是局部的，这就给IB-LBM 的并行化提供了良好的条件。Valero-Lara等［7］将IB-LBM 在基于图形处理器（Graphics Processing Unit，GPU）的异构平台上进行优化，改进内存管理和降低主机与加速器通信的成本；Lorenz 等［8］提出一种新的加速方法，即在GPU 上执行LBM 模型和流固耦合计算，并通过消息传递接口（Message Passing Interface，MPI）对共享内存资源上的计算进行并行化。虽然在GPU 上模拟IB-LBM 可以取得很好的效果，但是由于IBM的部分并行性较低，这一部分的开销会降低并行计算的总体性能；并且在GPU 上模拟IB-LBM 还会受到带宽的限制，也会影响计算的性能。另一种并行优化的方式，是采用共享存储并行编程（Open Multi-Processing，OpenMP）。OpenMP 进行并行计算时，各个线程间共享内存，因此比较适合于共享内存结构的单台计算机。在多核中央处理器（Central Processing Unit，CPU）结构上，具有效率高、内存开销少的优势，且编程语句简洁直观，易于编程。

针对IB-LBM 模拟大规模或密集网格时，模拟时间长、效率低下的缺陷，针对IB-LBM 局部计算的特点，通过OpenMP中的编译制导语句将IB-LBM 并行化。但直接将IB-LBM 作并行化，是一种粗糙的并行化，为此在并行化的基础上还提出了进一步的优化策略，即将IB-LBM 进行了整体上的结构化分解，对每一结构部分测试不同任务调度方式的优化性能。在不同的线程数下，即2 核、4 核、8 核、16 核下，分别进行大量实验和分析后，得到了每一线程数下最优的组合策略。

1 浸入边界-格子玻尔兹曼方法

IB-LBM 在模拟流体流过移动边界或复杂边界的情况下，是一种比较灵活且高效的计算，它的计算区域由两类格点组成——拉格朗日点和欧拉点（Eulerian Point）（见图1）。其中：欧拉点表示整个流场，拉格朗日点表示浸入物体的边界，通过边界的形变计算物体受力，即恢复力，再使用狄拉克函数（Dirac Delta Function）将恢复力离散到流场的欧拉点上，最后求解流场的宏观密度和速度。

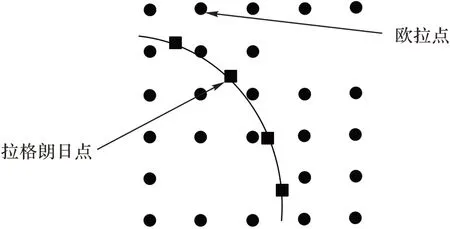
图1 IB-LBM模型二维流场边界结构Fig.1 2D flow field boundary structure of IB-LBM model

IB-LBM 模型中求解流场部分应用最广泛的模型，是由Qian等［9］提出的DnQm（n是空间维数，m是离散速度数）模型，在二维的情况下，最常用的是D2Q9 模型，如图2 所示，其中ei和fi分别为离散速度方向和分布函数方向。

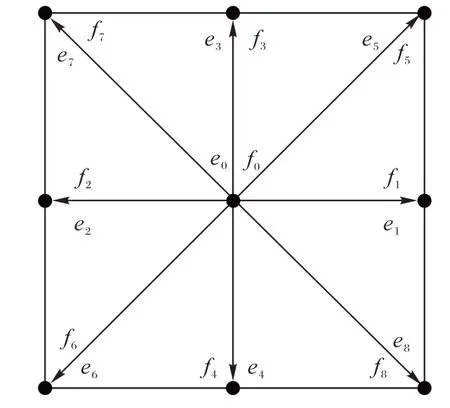
图2 D2Q9模型的局部结构Fig.2 Local structure of D2Q9 model

对于流场的碰撞和迁移步骤可以表示为：

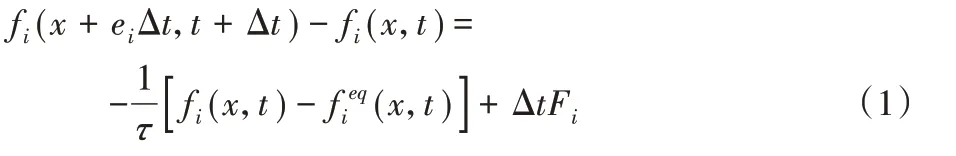
其中：fi(x，t)为粒子分布函数；x和t分别为当前粒子所在的格点位置和当前的格子时间；ei为D2Q9模型中的粒子离散的方向；Δt 为格子时间步；τ 为松弛时间，它的取值由流体的运动黏性系数μ（见式（2））决定。

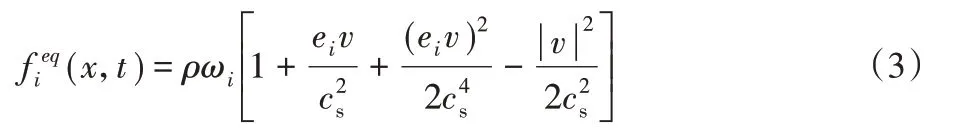
其中：v为当前格点上的宏观速度，ωi是离散速度的权重系数，ei是离散方向。在D2Q9模型中，各参数的取值为：

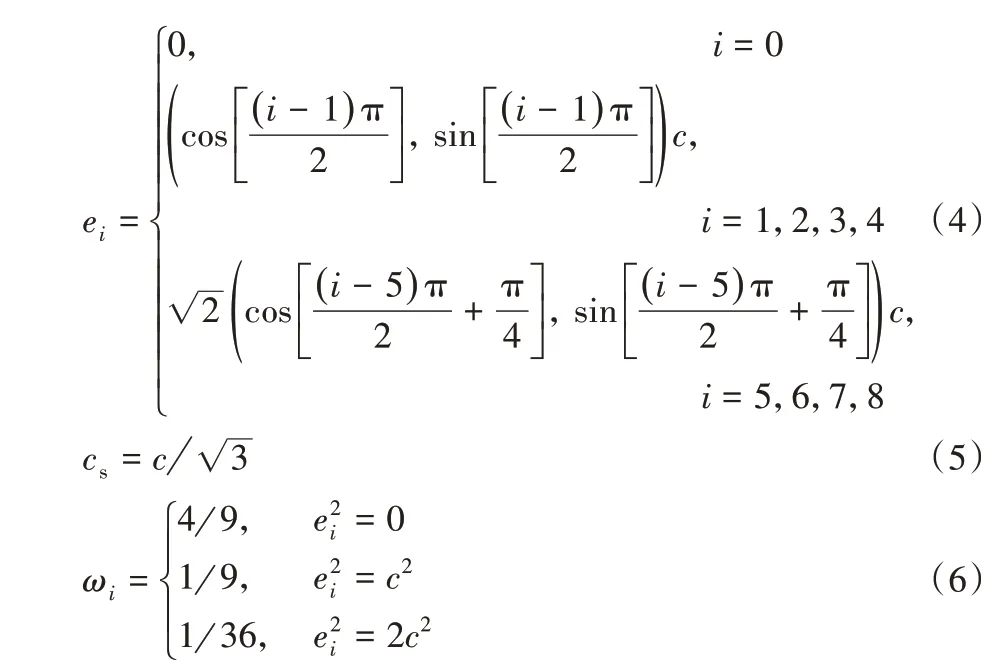
在流场的碰撞迁移过程中，边界的计算要进行单独的处理。在平直边界条件的情况下，针对边界条件，本文采用了非平衡态外推格式［10］，其表达式为：

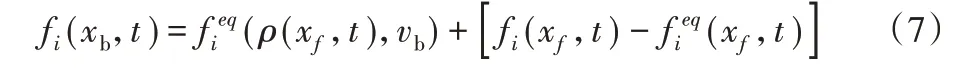
其中：xb为上下边界的边界格点，ρ(xf，t)代表边界格点xb的相邻格点xf的密度，vb为边界格点xb的速度。

在求解IB-LBM 模型的过程中，核心问题是拉格朗日点上力的计算和插值。对于恢复力的计算，本文应用的为惩罚力计算方法［2］。惩罚力法的基本思想是应用胡克定律（Hook’s law），将浸入物体的边界看作是由拉格朗日点组成的弹性边界，且该边界具有合适的刚度系数ε。物体受力产生形变，拉格朗日点的位置移动到参考点的位置（图3），通过胡克定律来计算因形变产生的恢复力：

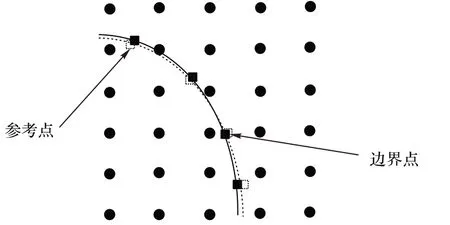
图3 物体形变的边界点和参考点Fig.3 Boundary point and reference point of object deformation

在计算过程中，拉格朗日点的位置是不变的，在每个格子时间步后，通过狄拉克函数来计算拉格朗日点移动后的参考点的位置。流场中体积力F(x，t)，通过边界点上的恢复力Fb插值到流场的格点上来得到，其表达式为：

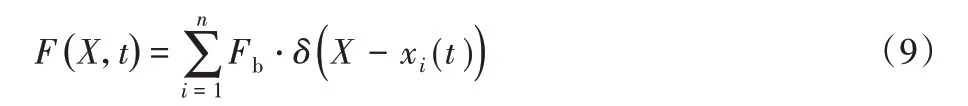
其中：X 为流场中的欧拉点；xi为边界上第i 个拉格朗日点；Fb为相应的恢复力；n 是边界上拉格朗日点的总数是一个狄拉克函数，可以通过该函数将边界点上的恢复力插值到流场的欧拉点上。狄拉克函数有多种表达式，本文使用的为：

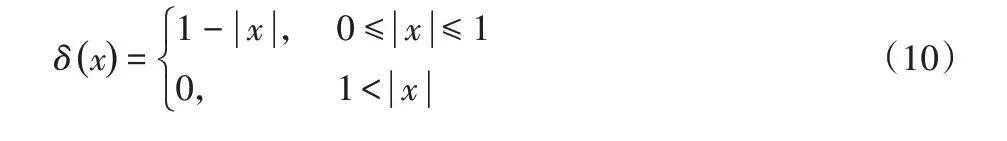
将物体边界点上的恢复力插值到流场的欧拉点上之后，需要根据所采用的DnQm 模型，将欧拉点上的体积力进行离散［11］，其表达式为：

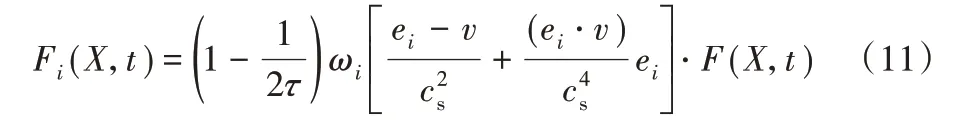
根据上述公式的计算后，流场中每个格点的宏观密度和速度表达式为：

求得流场的宏观速度后，通过狄拉克函数，可以求得边界点上拉格朗日点的速度，其表达式为：

其中：vi为边界上第i个拉格朗日点的速度，X为流场中的欧拉点，v(X，t)为相应的欧拉点的速度，N 为流场中欧拉点的总个数。求得边界点的速度后，即可求得受力形变后，拉格朗日点移动后的参考点的位置：

最后，总结IB-LBM的计算步骤为：

1）设置流场及浸入边界的初始参数，包括流场的大小、流场的初始密度、流体在入口处的初速度、浸入边界的大小和位置等。

2）通过式（8）计算浸入边界的恢复力，并应用式（10）将力插值到流场的欧拉点上。

3）将欧拉点上的力用式（11）进行离散，然后执行式（1），进行流场的碰撞迁移；与此同时，在迁移时执行式（7），对流场的边界进行单独的处理。

4）执行式（12）和式（13），计算流场的宏观密度和速度。

5）应用式（14），将欧拉点的速度插值到边界点上；然后执行式（15），计算拉格朗日点移动后，相应的参考点的位置。

6）回到步骤2），进行下一个格子时间步的演化，直到达到规定的时间步。

2 并行优化策略

在使用IB-LBM 进行问题模拟时，由于要得到稳定、准确的模拟结果，所以流场要进行多次演化，那么程序的负载均衡问题是影响程序性能的首要问题之一。在OpenMP 的并行优化中，提供了三种任务调度方式：静态调度（static，以下简称为s 调度）、动态调度（dynamic，以下简称为d 调度）、启发调度（guided，以下简称为g调度）。通过调节各线程的任务调度方式，优化线程的计算负载，以充分利用线程资源，提高程序计算性能。

s调度方式，同样也是当程序中for或者parallel for 制导指令没有选择调度方式时，程序默认的调度方式。s调度在编译时已经确定某一线程将要执行哪些迭代。假设计算任务为T个线程执行N 次迭代循环，那么每个线程分配到的计算任务约为连续的次迭代。

d 调度方式，线程动态申请计算任务，即当线程的计算任务完成后，继续申请下一组计算任务。虽然d 调度可以避免平均分配所带来的负载不均衡问题，但线程的任务动态申请会造成额外的开销。

g调度方式，在程序开始时会给每个线程分配比较多的计算任务，之后每次分配给线程的计算任务会按指数级下降。

为了便于对IB-LBM 进行并行优化，首先根据计算步骤将IB-LBM 进行结构分解（如图4），分解后每一部分都是独立的，在结构块内部不存在数据依赖，只在结构块与结构块之间存在数据依赖。

图4 IB-LBM结构分解Fig.4 IB-LBM structural decomposition

算法并行最难的问题之一是要保证各个处理器的负载均衡，并减少计算资源浪费的情况。将IB-LBM 结构分解后，可以看出，恢复力的计算和参考点位置的计算这两个结构块的计算量大小与边界点的数量成正比关系。在计算规模较小，即边界点数量较少的情况下，不宜进行算法的并行，因为并行计算后的总时间，包括线程的开辟与销毁、任务调度的开销以及任务进行计算的时间，将大于串行计算的时间，起不到优化效果；而在计算规模较大，即边界点较多的情况下，由于s 调度和g调度的任务调度的调度开销要小于d调度，且两个结构块的计算任务简单，各线程的处理速度大致相同，因此恢复力的计算和参考点位置的计算两个结构块适合使用s 调度或g调度。对于体积力的计算、碰撞和迁移、边界处理、宏观量的计算四个结构块，其计算量大，且计算任务复杂，导致各个线程的计算任务结束的时间不同，有快有慢。为了避免出现资源浪费，即出现线程空闲的情况，需要根据线程的计算情况，及时地为线程分配计算任务。在三种任务调度方式中，d 调度和g 调度这两种调度方式更加灵活，可以根据各个线程的完成情况，及时为空闲线程分配计算任务，因此，体积力的计算、碰撞和迁移、边界处理、宏观量的计算四个结构块更适合于应用d调度或g调度。

根据上述内容，逐一测试三种调度方式，在IB-LBM 的每一结构步骤中，并行性能最佳的调度方式被挑选出。经过大量的实验和对比分析后，选择出整个IB-LBM 并行性能最优的混合调度方式。之后，根据上面的实验方式，测试不同线程数下的并行性能最优的混合调度方式。实验结果如表1。由表1 可以看出，使用较多的是d 调度和g 调度。虽然d 调度动态申请计算任务的方式会造成额外的时间开销，且g 调度缺乏一定的灵活性，但在三种调度方式中，这两种调度方式的优化性能更好一点。因此在使用不同数量的线程模拟时，这两种调度方式的应用比较多；而s 调度相对于其他两种调度方式，灵活性最差，导致其计算效率较低。

表2 详细记录了最优策略下的加速比，同时与理想状态下的加速比和应用单一任务的加速比进行了比较。

从表2 可以看出，在线程数量较少的情况下，实际的加速比接近理想状态的加速比。随着线程数量的增多，线程的开辟和销毁带来的额外时间开销，以及任务调度的时间开销，对模型执行的整体效率的影响也逐渐加大，但整体的优化效果仍是比较好的，并行计算的性能有了大幅度的提高。同时，在线程数量较少的情况下，多种任务调度方式混用的优化效果与单一任务调度方式优化效果差距很小，可以得出结论：在线程较少的情况下，任务调度方式对优化效率的影响不大。在线程数量较多的情况下，应用单一任务调度与多种任务调度混合的优化效果差距比较明显；在整体上，d 调度方式与多种调度方式混用的优化效果差距很小。

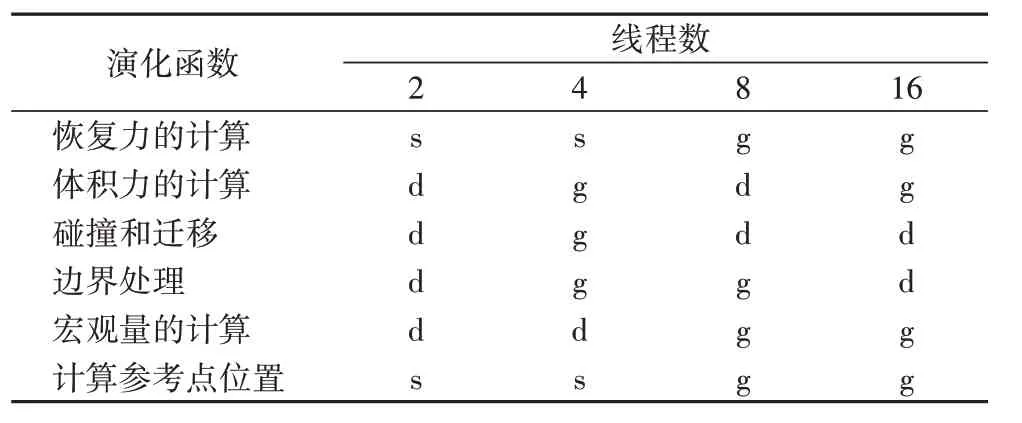
表1 多种任务调度方式混用的最佳组合Tab.1 The best combination of multiple task scheduling modes

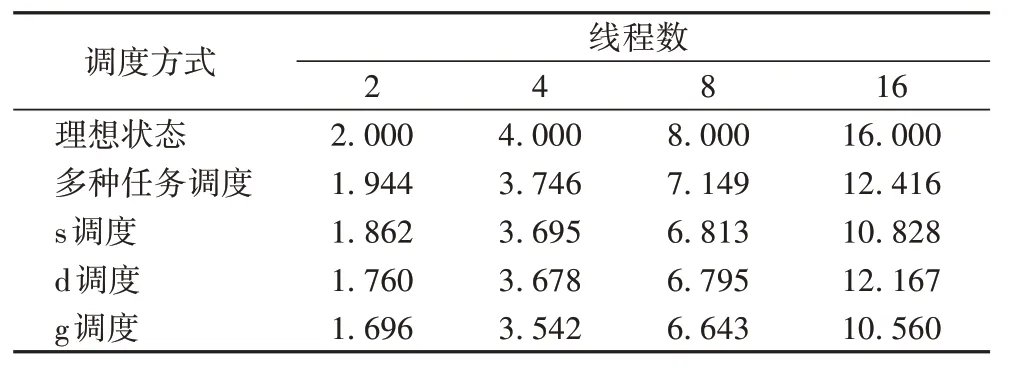
表2 理想状态、多种任务调度与单一调度的加速比Tab.2 Speedup of ideal state，multiple task scheduling and single scheduling

表3 中为多种任务调度最优组合下，不同的流场规模在不同线程数量时，具体的加速比数值。从表3 可以得出结论：在流场规模较小的情况下，线程的开辟和销毁，以及任务调度所造成的额外时间开销，在总的运行时间中影响较大，降低了并行效率；而在流场规模较大的情况下，额外的时间开销在总时间中的占比较小，因而对并行效率的影响较小。

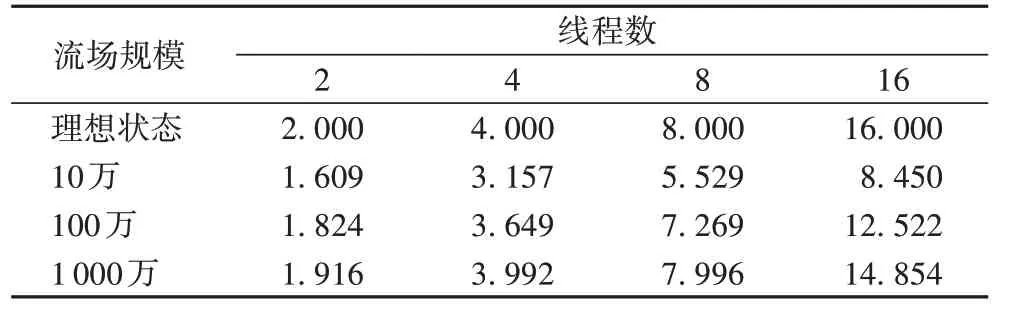
表3 理想状态和不同流场规模的加速比Tab.3 Speedup of ideal state and different flow field scales

3 实验模拟与分析

本章将模拟一个圆柱绕流问题。在流场的几何结构上，设置圆柱的直径大小为D，流场的大小为40D×15D，几何结构如图5。

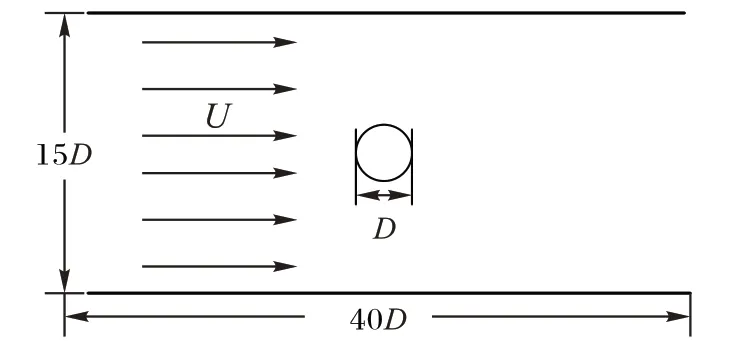
图5 流场几何结构Fig.5 Flow field geometrical structure

实验环境为Red Hat Enterprise Linux 6.3 操作系统，应用GCC 4.4.6编译器进行编译。硬件设施是Intel E5-4650 CPU，主频为2.7 GHz，内存为512 GB RDIMM DDR3 1 600 MHz。

求解流场过程中，进行碰撞时为全部格点进行碰撞，流场格点进行迁移，对边界格点进行额外的处理。在边界处，采用非平衡态外推格式的边界处理条件。在整个流场的入口处，在每个格点X 方向上添加一个初速度U。流场中，流体的流动情况可以用雷诺数（Re）来表示，计算雷诺数的表达式为其中：ρ 为流体的密度，设置流场的初始参数时，一般将ρ 设置为1.0，之后ρ 会随着流场的演变而变化；U为流场中在入口处设置的流体的初速度，本文中U=0.1；D为圆柱的直径；μ为流体的黏度系数。

从流场的模拟效果图（图6）中可以看出，随着流场的演化，圆柱绕流的流场演化过程达到稳定状态时，圆柱靠近入口处会形成高压区域，在圆柱的两侧会交替形成低压区域，即圆柱上下两侧交替出现脱落涡。

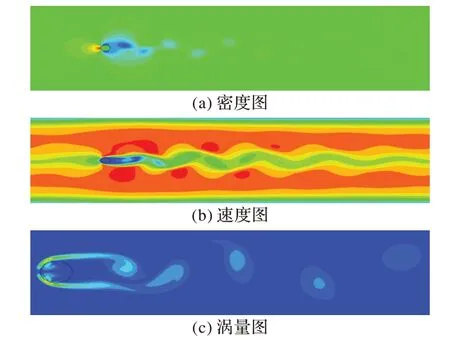
图6 流场的模拟效果图Fig.6 Simulation of flow field

图7 为流场在不同时刻的流线图。其中T 为无量纲时间尺度，其计算公式为：

其中：U 为流场的入口速度，t 为当前的格子时间，D 为圆柱直径。

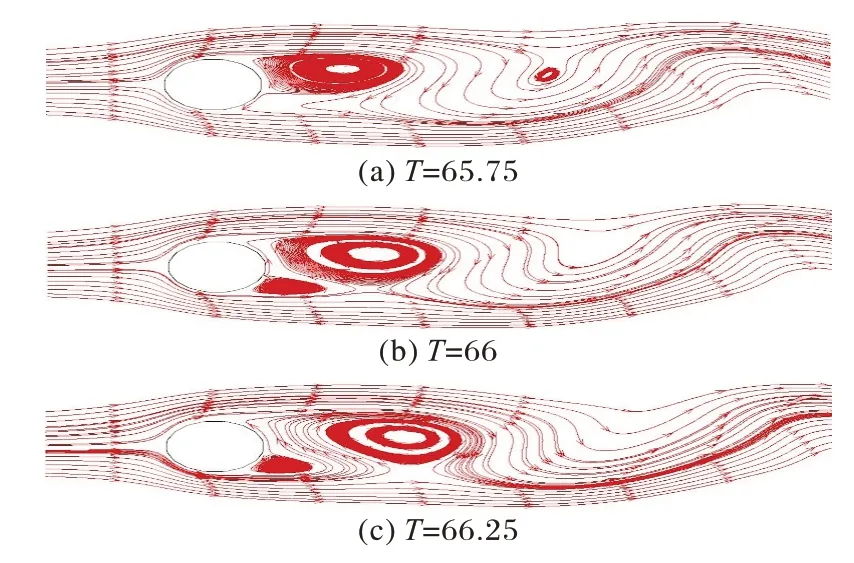
图7 流场在不同时刻的流线图Fig.7 Streamlines of flow field at different times

从图7 中可以观察得出，在圆柱周围，没有流线渗透进入到圆柱中，与实际情况相符，说明圆柱边界与流场实现了无滑移边界，因此，可以说明IB-LBM 对于模拟圆柱绕流问题是比较准确的。

为了进一步验证本文所提方法的准确性，将给出圆柱绕流问题在Re=20 和40 情况下的阻力系数、回流区域长度（L，L的度量尺度为圆柱的半径），并与基于平滑轮廓-格子玻尔兹曼 方 法（Smoothed Profile-Lattice Boltzmann Method，SPLBM）［12-14］的计算结果进行对比，结果如表4 所示。从表4 中可以看出，本文优化方法所计算出的结果与对比文献中的计算结果一致。针对圆柱绕流问题在Re=100 和200 时，即流场不稳定流动的情况下，给出了阻力系数与斯特劳哈尔数(St)的计算结果，并与采用其他数值模拟方法［15-19］来计算圆柱绕流问题的文献方法的计算结果进行对比，结果如表5。从表5 中可以看出，本文的阻力系数和St 与文献中的计算结果保持一致。图8展示了雷诺数为200时，阻力系数和升力系数随时间变化的曲线，曲线呈周期性变化，验证了流场模拟结果的准确性。。

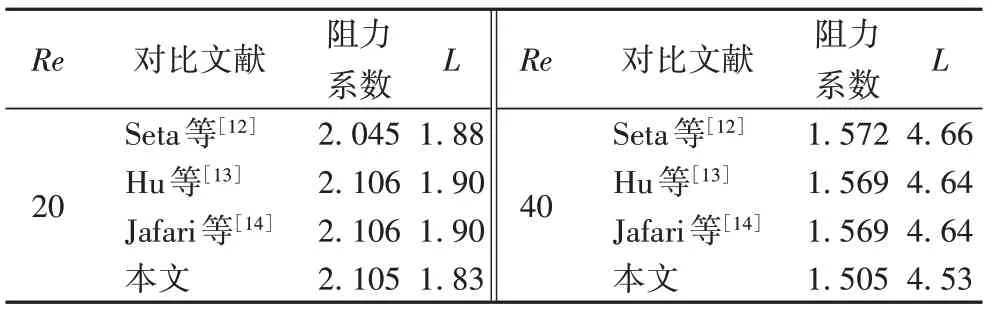
表4 Re=20，40时阻力系数和回流区域长度（L）的对比Tab.4 Comparison of drag coefficient and recirculation zone length（L）when Re=20，40

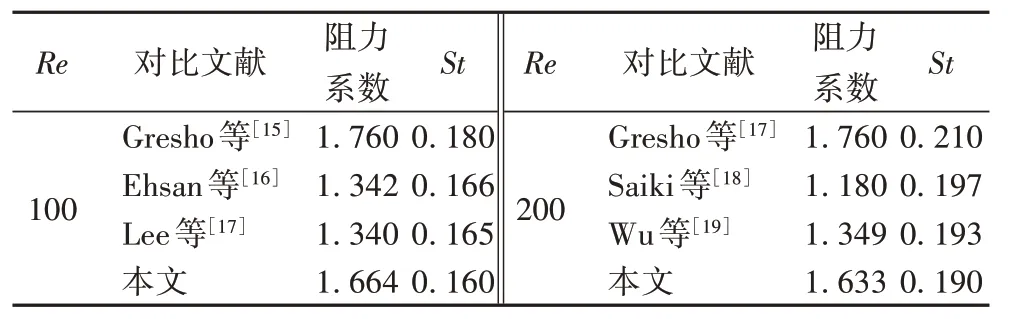
表5 Re=100，200时阻力系数和斯特劳哈尔数（St）对比Tab.5 Comparison of drag coefficient and Strouhal number（St）when Re=100，200

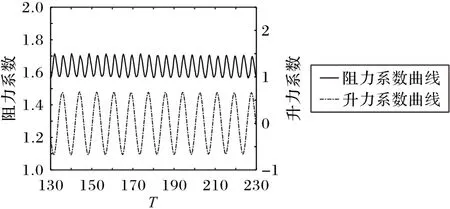
图8 Re=200时阻力和升力系数变化曲线Fig.8 Drag and lift coefficient change curves when Re=200

4 结语

本文通过OpenMP 编译处理方案对IB-LBM 并行计算的性能问题进行了并行优化，并针对OpenMP 中不同类型的任务调度方式：s调度方式、d 调度方式、g 调度方式，进行了实验测试。使用单一的任务调度时，只能对IB-LBM 进行粗粒度的并行优化，并行性能较低，因此进一步采用多种任务调度混合使用的方式对IB-LBM 进行了新的细粒度的并行优化。通过将IB-LBM 结构化分解，并对各结构步骤进行并行优化，测试三种任务调度的优化性能。通过上述实验方法，在进行大量实验和分析后，得出了在不同数量的线程参与模型的并行计算，即2 核、4 核、8 核、16 核的情况下，三种任务调度方式混合使用的最优组合策略。优化结果通过加速比来直观地展示，可以得出，在使用的线程数量不同的情况下，多种任务调度混合使用的最优组合方式是不同的：在2 核和4 核的情况下，混合任务调度的优化效果差距不大，加速比接近理想状态；在8核、16 核的情况下，由于开辟线程和任务调度的额外开销，对优化后的计算性能产生了影响，但并行性能仍是较好的。同时实验得出，线程较多的情况下，在放大规模后，由于额外的时间开销在总的执行时间中产生的影响降低，加速比也有较大的提升。虽然本文对IB-LBM 进行了效果比较好的优化，但IBM 部分的优化效果仍然不高，有待进一步研究。