基于分布式神经网络的苹果价格预测方法

刘 斌，何进荣，李远成，韩 宏

（1.西北农林科技大学信息工程学院，陕西杨凌712100；2.农业农村部农业物联网重点实验室（西北农林科技大学），陕西杨凌712100；3.陕西省农业信息感知与智能服务重点实验室（西北农林科技大学），陕西杨凌712100；4.延安大学数学与计算机科学学院，陕西延安716000；5.西安科技大学计算机科学与技术学院，西安710054）

0 引言

中国是世界上最主要的苹果生产大国，苹果产量约占世界苹果总产量的55%。同时，苹果营养丰富［1］，不仅可以调节肠胃功能，还具有降低胆固醇、增加记忆力和防癌等功效。开展苹果市场价格的短期预测性研究，对果农规避市场风险、提高管理部门市场宏观调控效率、切实保护消费者权益和保障苹果市场稳定具有重要的理论意义和应用价值。针对这一问题，学术界已经提出多种苹果市场价格短期预测模型。然而，现有的预测模型都是基于串行算法实现的，比较耗时，且随着大数据时代的到来，无法快速准确预测海量数据场景下的苹果市场价格。因此，本文基于云计算平台通过大数据切分的形式，训练了多个神经网络模型，并将预测结果采用求取平均权值的形式对多个神经网络模型进行融合，在海量数据的场景下有效地利用并行机制设计和实现了复杂度低、并行度高的苹果市场价格短期预测模型。

1 相关研究

近年来，国内学者和科研人员针对农产品市场价格短期预测展开了广泛的研究。较早被应用于农产品价格预测的模型有自回归积分滑动平均（AutoRegressive Integrated Moving Average，ARIMA）模型［2］和组合模型［3］。刘峰等［2］以白菜月价格数据为研究对象，基于ARIMA 模型预测白菜未来的月价格，实验结果表明，ARIMA（0，1，1）模型能很好地模拟并预测白菜月价格趋势，为农产品市场信息准确预测提供了重要方法。王川等［3］以我国苹果市场价格为研究对象，综合双指数平滑模型、Holt-Winters 乘法模型和ARIMA 模型提出了一种组合预测模型对苹果市场价格进行预测，实验结果表明组合模型预测的精度高于单项时间序列模型。丁慧娟等［4］以遵义猪肉价格为研究对象，通过对ARIMA 模型和灰色模型两种模型具体步骤进行分析，实现了对猪肉价格的精准预测，提高了经济效益。ARIMA、组合模型等时间序列模型单纯依靠历史价格进行预测，用不同的模型根据相同的价格信息往往得到不同的结果，未能有效利用尽可能多的有效信息。为了综合考虑其他因素对农产品价格的影响，科研工作者提出采用多元线性回归、神经网络等模型对农产品价格进行预测。钱晔等［5］以蔬菜瓜果为研究对象，将菜蔬价格分为高价、较高价、适中、较便宜以及非常便宜5 类，通过聚类分析法比较测试数据与5 类目标距离对像的距离，实现了对蔬菜瓜果的预测。姚冠新［6］针对农产品价格序列具有非线性特征，以全国苹果周批发价格序列为研究对象，提出一种基于经验模态分解和支持向量机的短期预测方法，对苹果批发价格进行了预测，实验结果表明该预测模型能够较好地预测农产品价格。张永礼等［7］提出一种基于模糊信息粒化和粒子群优化支持向量机的农产品价格预测时序回归模型，实现了对棉花价格的预测。Zhang等［8］研究农畜产品价格的影响因素，采用多元线性回归的方法建立了农业和畜牧业产品价格的预测模型，该模型可以提前预警由于突如其来的自然灾害引起的农作物减少和价格上升可能引发的问题。许杞刚等［9］针对农产品价格波动特点，基于改进的K 最近邻（K-Nearest Neighbors，KNN）算法构建了农产品价格预测模型，实验结果表明该预测模型具有较高的预测精度，满足农产品价格预测的要求。苏照军等［10］结合BP（Back Propagation）神经网络和支持向量回归机（Support Vector Regression，SVP）的组合模型构建了一种新型农产品物价预测模型BP-SVR-BP，实验结果表明该模型预测精度更高，能够客观真实地反映农产品物价变化规律。段青玲等［11］提出一种基于时间序列遗传算法（Genetic Algorithm，GA）和SVR 的预测模型对水产品价格进行预测，实验结果表明其预测结果同真实值相比误差极小。罗长寿［12］利用蔬菜的价格数据，基于BP 神经网络模型、基于遗传算法的神经网络模型和径向基函数（Radial Basis Function，RBF）神经网络模型建立了一种集成的网络预测模型，实现了对蔬菜价格的预测，实验结果表明，该集成预测模型能够提高蔬菜市场价格的预测精度，效果比单一的预测模型更好。相比单变量回归模型，多元线性回归、神经网络模型以及集成模型在农产品市场价格预测方面虽取得了较大的成功，但目前研究采用的串行算法在单台计算机上需要很长的运算时间，导致计算代价高，无法实时响应；同时，由于单台计算机存储容量不足，导致存储墙问题，无法将所有的数据载入内存进行迭代计算，串行算法无法适应基于大数据分析的苹果市场价格预测场景。在大数据环境下针对我国苹果产业构建分布式神经网络模型进行市场价格短期预测还处于空白领域，是当前人工神经网络和农业信息化领域的一项重要研究工作。

2 预测模型构建

本文以陕西白水、洛川、千阳和全国苹果市场价格为研究对象，研究影响苹果市场价格波动规律的相关因素，选取苹果历史价格、替代品价格、居民消费水平和原油价格为特征，构建蕴含价格波动规律的分布式神经网络预测模型，实现对苹果市场价格的短期预测，探讨适合我国苹果市场价格短期预测方法，以探索苹果市场价格的预见性，避免苹果市场价格波动带来的危害，同时也为其他农产品市场价格的短期预估提供不同的思路。

2.1 相关因素分析与数据来源

苹果市场价格是由多种因素的影响共同决定的，经过市场调研分析，苹果的市场价格主要与以下因素［13］相关：1）历史价格。根据经济学价格规律，市场未来的商品价格围绕着历史价格上下波动。2）替代品价格。苹果市场价格受到供求关系的影响，根据经济学理论替代效应，苹果的替代品会导致消费者对苹果的需求失衡，引起苹果市场价格变动。3）居民消费水平。根据经济学收入效应理论，收入水平的实际变动能引起商品价格的变动。4）运输成本。苹果产地不同，距离消费市场的距离不同，会引起运输成本不一致。运输成本主要由油价决定，因此，本文研究将油价作为一种影响因素。5）地域分布。苹果价格的地域分布差异十分明显，分析调研数据结果显示，近产区或者大产区价格一般要低一些，而远离产区或者较小的分散产区价格也会相对较高。6）季节变化。由于所处时期的不同，价格存在明显的波动，在苹果的成熟季节价格较低，而较远离这个时期价格就较高。7）突发事件。自然灾害等突发事件能大幅度影响价格波动，但难以计量和预知。

上述7 个因素会影响苹果市场价格的波动，通过分析历史数据这一因素后发现，地域分布和季节变化对苹果市场价格的影响蕴含在历史数据中，所以本文研究将历史价格作为独立特征。同时，由于突发事件对市场价格的影响较为复杂，难以建模，在阶段性的工作研究中暂不考虑。

在数据来源方面，全国苹果价格和替代品梨价格来源于一亩田网站，居民消费水平来源于中华人民共和国统计局，原油价格来源于黄金网，陕西白水、洛川和千阳的苹果价格数据由西北农林科技大学苹果实验站价格信息员采集上报。经过对以上数据源进行数据预处理形成实验数据集（记录了2016年1月8日—8月12日的相关特征数据）。

2.2 特征设计与数据预处理

通过对苹果市场价格的影响因素的分析和提取，最终确定影响苹果市场价格的4 个因素为：苹果历史价格、替代品梨历史价格、居民价格消费指数和原油价格，并将这4 个影响因素作为神经网络模型输入层的特征。在数据预处理时，苹果历史价格、替代品历史价格和原油价格数值精确到小数点后两位。居民消费水平以居民消费价格指数（Consumer Price Index，CPI）表示，数据来源于中华人民共和国国家数据网（http：//data.stats.gov.cn/），由于居民消费价格指数以月度进行统计，因此，本文通过差值法将月度居民消费指数转换成日度居民消费指数。此外，为了消除具有不同量纲的特征值对数据分析产生的影响，对数据进行了归一化处理。

2.3 神经网络模型

设定神经网络为三层结构，即1个输入层、1个隐藏层和1个输出层。输入层节点数目由实际输入的特征数量确定。输出层节点数由目标输出特征个数确定为1 个节点。隐藏层节点数由经验方法式（1）确定。

其中：m 为输入层神经元节点数目，n 为输出层神经元节点数目，a为0～10区间的常数。该公式的值是一个区间，具体值根据问题的复杂度和对预测精度的要求由实际测试确定，本文研究中根据实际测试结果取值为6。

根据以上分析，最终确定的苹果市场价格神经网络预测模型结构如图1所示。针对神经网络模型作以下定义：L表示神经网络的层数；nl表示l层神经元的个数；fl(·)表示l层神经元的激活函数；W(l)∈Rnl×nl-1表示l-1 层到第l 层的权重矩阵；b(l)∈Rnl表示l-1 层到第l 层的偏置；z(l)∈Rnl表示l 层神经元的状态；a(l)∈Rnl表示l层神经元的激活值。

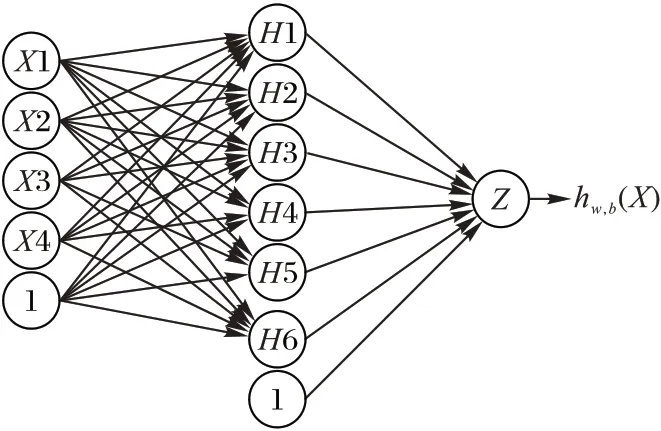
图1 神经网络预测模型Fig.1 Neural network prediction model

2.4 分布式神经网络模型设计与算法

本文提出的分布式神经网络模型设计如图2 所示：分布式神经网络模型能对大数据进行分解，同时，将训练模型的计算量分摊在多个计算节点上并行计算以加快收敛，最后将中间结果组装成最终解，对苹果市场价格进行预测。

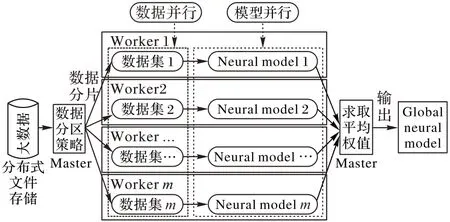
图2 分布式神经网络模型Fig.2 Distributed neural network model

在训练过程中采用的分布式神经网络算法如算法1 所示，在Spark分布式计算框架中首先在Master节点设置全局神经网络模型参数，主要包括神经网络结构、网络层数、激活函数、学习率因子和网络权重。然后，采用数据划分策略将较大的数据集D 划分成m 等份数据集。最后，将全局神经网络模型结构和参数广播至各Worker 节点。各Worker 节点接收到Master 节点传来的权重参数后对各自神经网络结构进行初始化，并利用式（2）和式（3）进行前馈计算，通过逐层的信息传递和计算，得到前馈神经网络最后的输出y（aL）。

假设给定一组样本(x(i)，y(i))(1 ≤i ≤N/m)，前馈神经网络的输出为f(x|w，b)，则目标函数为式（4）：

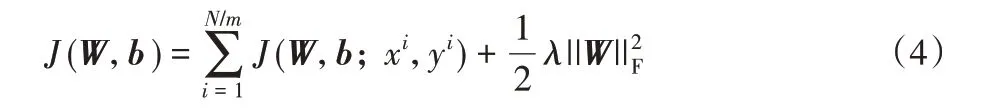
为了最小化目标函数J(W，b)，采用梯度下降法更新参数，如式（5）和式（6）所示：

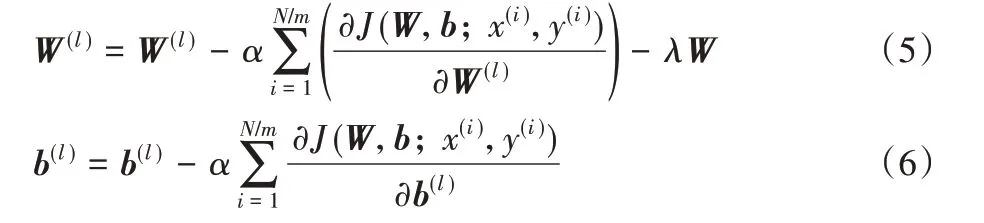
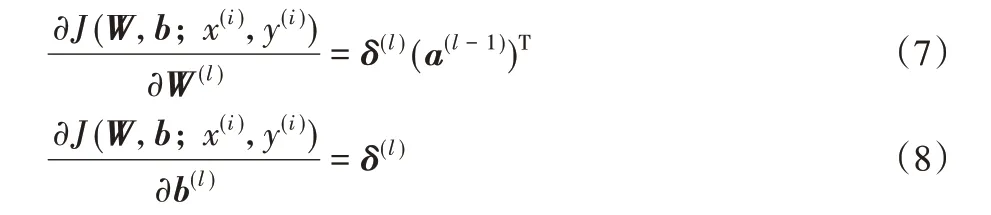
而δl通过式（9）计算：

其中·是向量的点积运算符，表示每个元素相乘。由式（9）可以看出，第l 层的误差项可以通过第l+1 层的误差项计算得出，第l 层的一个神经元的误差是所有与该神经元相连的第l+1 层的神经元的误差项权重之和乘上该神经元激活函数的梯度。

将反向计算得出的δl代入式（7）和式（8），求取神经网络各层的导数，并利用式（5）和式（6）对权重及偏置进行更新，最后输出分布式神经网络模型参数。

算法1 分布式神经网络算法。

输入 训练集(xi，yi)(i=1，2，…，N)，迭代次数T；

输出 W，b。

1） 设置神经网络模型参数（神经网络结构、网络层数、激活函数、学习率因子等）；

2） 初始化权重：w0=0；

3） 采用数据分区策略将大数据集D 划分成m 等份数据子集Di；

4） 在Master 节点上向各Worker 节点分发全局神经网络模型结构及参数；

5） for t=1，2，…，T do

6） for i=1，2，…，N/m do

8） 利用式（2）、式（3）前馈计算每一层的状态和激活值，直到最后一层；

9） 利用式（9）反向计算每一层的误差δl；

10） 利用式（7）和式（8）求取每一层参数的导数；

11） 通过式（5）和式（6）更新参数，调整神经网络的权值；

12） end；

13）end；

14）Master 节点汇总Worker 节点发来的参数，并求取平均值得到全局参数，并返回神经网络模型。

神经网络模型不仅学习规则简单，具有较强的记忆能力和强大的自学习能力，同时具备很强的非线性拟合能力，可映射任何复杂的非线性关系［14-15］；但也存在比如过度拟合、收敛速度过慢和导致局部最优等问题。本文针对这些问题对神经网络模型进行了优化，优化的策略主要包括在训练数据集中加入随机噪声和采用Dropout 方法让神经网络模型中某些隐藏节点的连接权重系数不起作用来增强神经网络模型的健壮性，防止网络的过度拟合；同时，为了加快训练速度和避免局部收敛，本文根据训练过程中的结果来自适应地改变学习速率，从而得到最佳的分布式神经网络模型。

3 实验结果与分析

3.1 实验环境

本文采用Spark 大数据处理框架实现了基于分布式神经网络的苹果价格预测方法。实验平台由1 个控制节点（namenode）和3 个计算节点（datanode 1～3）组成，各节点之间以千兆以太网互联，Hadoop 采用2.6 版本，Spark 采用1.3 版本，其配置参考Hadoop、Spark 官方网站提供的方法进行搭建配置，实验环境如表1 所示，其中，分布式神经网络模型采用Scala编程语言和MapReduce编程模型实现。

3.2 实验结果与分析

为了验证本文所提模型和方法的性能，采用绝对误差和相对误差进行评估，其定义如下：

其中：Ea 为绝对误差，xi为单次预测值，Ti为真实值，n 为测试样本数量；Er为相对误差，是绝对误差和真实值的百分比率。

基于本文提出的分布式神经网络模型，选取2016 年8 月6 日—8 月12 日连续7 天的数据作为预测样本，预测是对苹果未来市场价格进行估计，但事实上本文研究采用测试集进行预测。利用真实数据值与预测值进行比较分析，进而评价神经预测模型的预测效果，以评估所提出的模型是否达到预期水平。同时，为了便于对照比较，将预测样本的预测值和真实值连接成为曲线，各地区测试样本结果如图3所示。

从图3 中可以直观地看出，各地苹果主产区市场价格的预测值大体上都能够逼近苹果的真实市场价格，绝大数预测点都能够较好地贴近真实值，其绝对误差始终保持在0.04元/斤之内；只有个别地区的个别数据点（样本137、样本271、样本272 和样本408）稍微有些偏差，与真实价格相差在0.05～0.06元/斤。

从图4 可以看出，各地区的相对误差曲线基本控制在一个较小的水平1%之下，但仍然有2个预测数据点的相对误差超过了1%的水平。实验结果表明，分布式神经网络模型具有较高的预测精度，能够使得绝大部分预测数据点都保持在较小的相对误差范围内。尽管个别数据点相对误差稍微有些偏差（实际上，相对误差最大也没有超过1.4%），但也说明个别数据点的预测偏差不会对其他预测点产生不良的影响，从而进一步验证了神经网络模型具有较强的非线性拟合能力和稳定性。

表1 实验环境配置Tab.1 Experimental environment configration

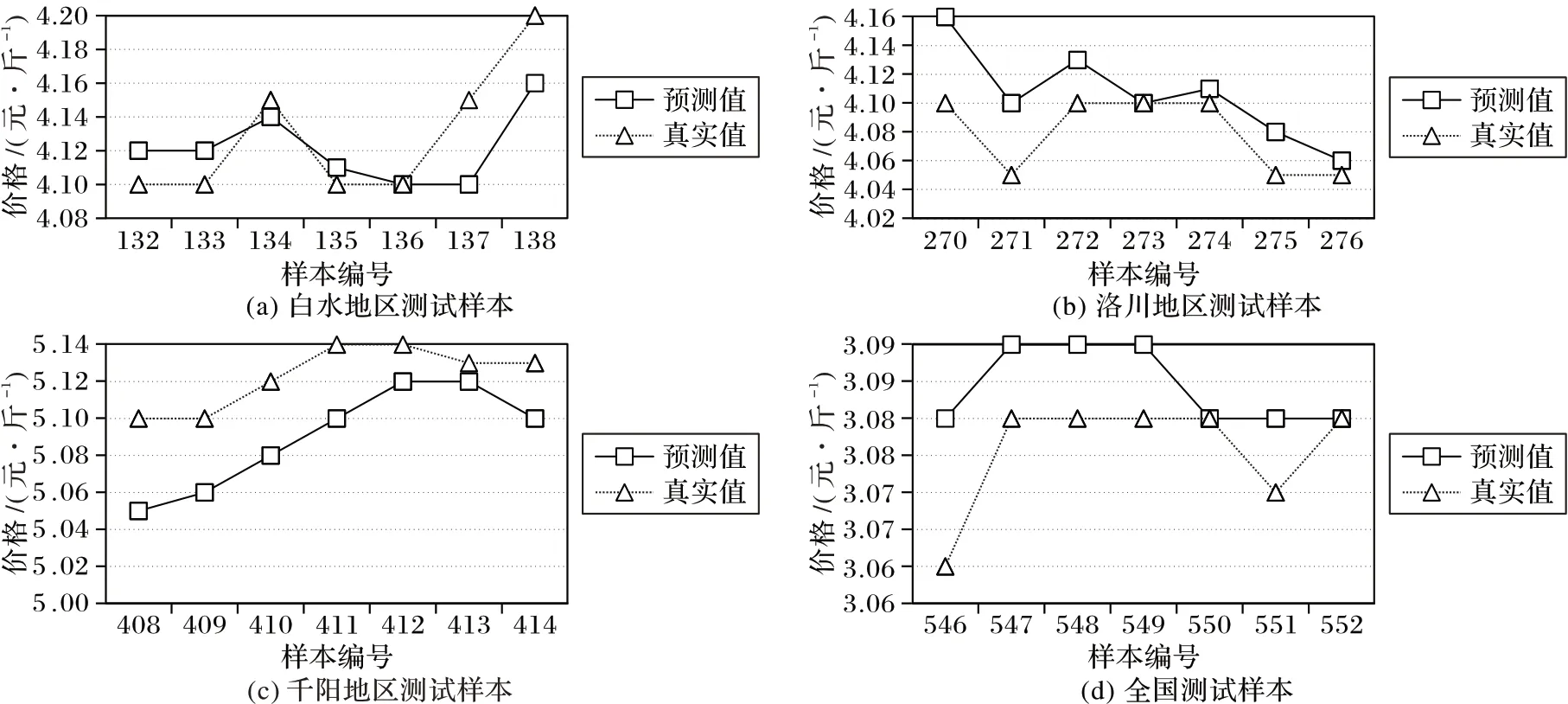
图3 不同地区与全国测试样本的真实价格与预测价格曲线Fig.3 Curves of prediction price and real price of test samples from different regions and the whole country

为了更加详细地对预测效果进行深度分析，以各产区的苹果市场价格预测过程为例进行具体评价。从表2 中看出，陕西省白水县苹果市场价格预测结果非常逼近真实价格，绝对误差绝对值超过0.02元/斤的仅有两个预测点，其他预测点偏差相对较小，其平均相对误差值为0.36%，处于非常小的水平。相比其他地区，陕西省洛川县苹果市场价格预测结果的误差最大；但绝对误差超过0.03元/斤的也仅有两个预测数据点，样本270和271绝对误差超过了0.05元/斤，相对误差超过了1%，其他预测点偏差相对较小。总体上来看，陕西洛川苹果的平均绝对误差保持在0.027 元/斤，平均相对误差值为0.66%，满足对苹果市场价格的预测要求。陕西省千阳县苹果市场价格预测结果相对较好，只有一个预测数据点的绝对误差绝对值超过了0.04元/斤，其他预测数据点的绝对误差绝对值和相对误差保持在较小的范围之内。但在千阳苹果市场预测时预测值均低于真实值，这说明基于分布式神经网络模型针对低估现象不存在自我修正机制。全国苹果市场价格预测结果相比其他地区预测效果最佳，绝对误差超过0.01元/斤的仅有一个预测数据点，其他预测点偏差都非常小，几乎可以忽略；其相对误差相应地也处于非常小的水平，其平均相对误差仅为0.28%，这样的预测结果近乎于“完全精准预测”。

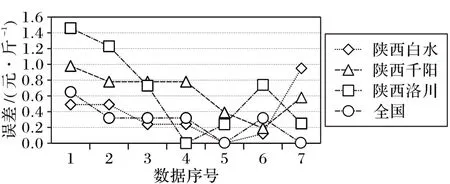
图4 各地区和全国数据的相对误差对比Fig.4 Comparison of relative error of different regions and the whole country

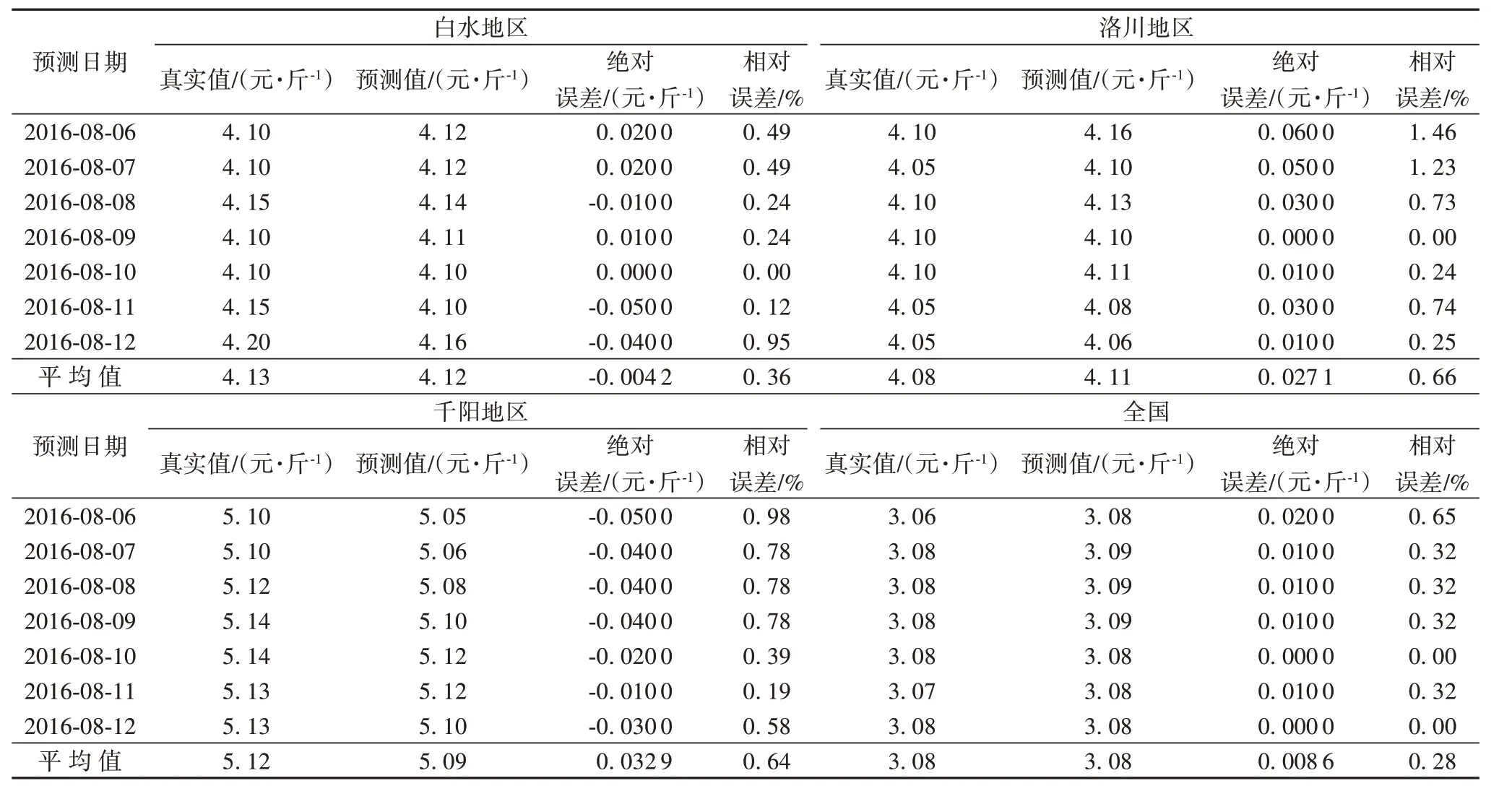
表2 各地区与全国的苹果价格预测结果与真实值Tab.2 Prediction results and true values of apple price in different regions and the whole country

4 结语

本文在海量数据场景下提出了一种基于分布式神经网络的苹果市场价格预测方法，在云计算平台下通过数据并行和规约求和的形式，训练了多个神经网络模型，并运用求取平均权值的形式对多个预测模型进行融合，为大数据环境下如何充分有效地利用云计算构建预测模型提供了一种思路。但本文研究目前仅仅考虑了可定量分析的相关因素，未考虑其他难以定量的因素，如：突发事件、金融危机、自然灾害、生产成本等。由于这些因素的不可预知性和难以定量分析，在本文的阶段性研究中没有考虑，在下阶段工作中有望将这些因素量化分析。