基于NSGA-II的多目标航材保障经费优化配置

张培

摘要：基于航材保障发付率来评估航材保障经费的配置效率，以总航材保障经费、总航材库为约束，以航材保障发付率的均值达到最大、方差达到最小为目标函数，建立多目标航材保障经费配置模型，利用快速非支配排序遗传算法（NSGA-II）求解案例，结果证明该模型是有效、合理的。

关键词：航材保障发付率；多目标规划；NSGA-II算法

Keywords：aircraft spares supply payment rate；multi-objective programming；NSGA-II algorithm

0 引言

航材保障的目的是为飞机定检、排故等维修工作提供所需器材，确保飞行安全、可靠，其基本任务是及时、准确、经济地供应所需的航材，保证训练、教学任务的完成。随着社会发展，飞机及其备件的购置费用已十分昂贵，为保障飞机正常使用所需的费用更是以惊人的速度增长。统计资料表明，在飞机及其备件的寿命周期费用中，飞机的维修保障费用约占50%～80%，但航材保障经费的增长却很有限。因此，如何利用有限的航材保障经费最大限度地提高航材保障系统的优化配置成为了一项重要的课题。

王斌 [1] 等以航材系统整体保障的提高和飞机维修器材费用的优化配置为目标，采用边际效益分析法建立了航材保障经费优化配置模型并求解。郭峰 [2] 等以航材保障经费为资源、以平均航材保障良好率达到最大为目标函数，建立了航材保障经费的优化配置模型，用动态规划的顺序解法进行求解。

本文着重考虑航材保障经费的优化配置效率，在不牺牲个别效率、使总体效率达到最大的前提条件下，建立多目标航材保障经费配置模型，将快速非支配排序遗传算法（NSGA-II） [3] 应用到模型求解中，并给出优化结果。

1 航材保障经费配置模型

航材保障发付率是指航材保障程度与维修需求程度的比值，在假设飞机定检、排故等维修工作理想化的前提下，可以直接反映航材保障对飞机维修的影响程度，进而可以有效地度量投入一定航材保障经费后飞行任务的完成程度以及经济效益。这里用航材保障发付率来评估航材保障经费的配置效率，目标是在不牺牲其他航材库航材保障发付率的前提下使航材保障发付率达到最大，即航材保障发付率的均值最大和方差最小。

1.1 模型中的参数

文中航材保障经费配置模型中使用到若干参数，现定义如下：

N为总航材库数量；xi为第i个航材库的保障经费；g为航材保障发付率；W为总航材保障经费；Z为所有航材库的平均航材保障发付率；S为所有航材库的航材保障发付率方差；σi为第i个航材库经费的期望；μi为第i个航材库经费的标准差。

1.2 航材保障经费配置模型的建立

航材保障发付率与航材保障经费之间存在一定规律，即航材保障经费投入越多，航材保障发付率越高。但是，随着航材保障经费的增加，航材保障发付率的增量逐渐减少。显然，航材保障经费服从以航材保障发付率的增量为概率密度的正态分布，其分布函数就是航材保障发付率。即

1.3 快速非支配排序遗传算法（NSGA-II）

以上模型为多目标规划问题，一般不可能存在一个使每个目标都达到最优的解。例如，所有航材库的航材保障发付率相等即方差最小时，航材保障发付率的平均值可能不是最大。所以多目标规划问题的解不是唯一的，而是一组均衡解，称为最优非劣解集或Pareto最优解集。

NSGA-II是最流行的多目标遗传算法之一，它降低了非劣排序遗传算法的复杂性，具有运行速度快、解集的收敛性好等优点，成为其他多目标优化算法性能的基准。

NSGA-II算法的基本思想为：首先，随机产生规模为N的初始种群，非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群；其次，从第二代开始，将父代种群与子代种群合并，进行快速非支配排序，同时对每个非支配层中的个体进行拥挤度计算，根据非支配关系以及个体的拥挤度选取合适的个体组成新的父代种群；最后，通过遗传算法的基本操作产生新的子代种群，依此类推，直到满足程序结束的条件。

2 算例分析

在某飞行训练学校的航材管理系统中有六个航材库，根据历年统计数据计算出航材保障经费的期望和标准差，如表1所示。该航材系统某年的航材保障经费为450万元。

本文求解的航材保障经费的配置问题可以转化为求满足等式约束和不等式约束的目标函数最小值优化模型，数学表达式为：

采用Matlab編写NSGA-II程序，应用上述模型。种群规模为200，交叉概率为0.8，变异函数为独立约束，采用锦标赛选择，进行到166代进化后，得到该多目标规划的Pareto最优解集，如图1所示。

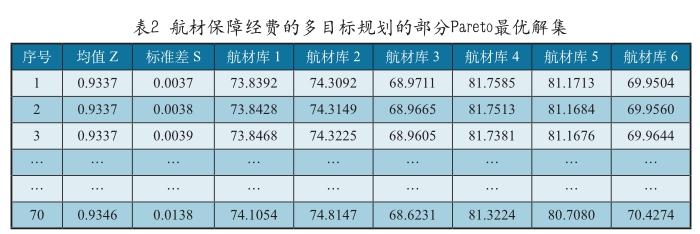
通过上述求解，共得到70个Pareto最优解，见表2。

本案例通过动态规划法、边际分析法得到的解为：平均航材保障发付率最大值为93.42%，方差为0.0161。最优解为（74，75，69，81，70）。由此可见，通过NSGA-II算法得出的Pareto最优解集更为精确，通过调整变量的更小数量级，可使平均航材保障发付率达到最大93.46%，方差达到最小0.0037。但是，如果将Pareto最优解集进行四舍五入，调整为整数，则所有Pareto最优解集都相同，且与通过动态规划法、边际分析法得到的解一致。

3 结束语

本文通过引入航材保障发付率来评估航材保障经费的配置效率，构造航材保障发付率均值最大、方差最小值的多目标规划模型，通过NSGA-II算法进行编程，求解得到Pareto最优解集，最后通过与动态规划法、边际分析法求得的解进行对比，验证了该模型、解法的有效性与合理性。本研究对航空公司以及维修单位航材部门的航材保障经费配置计划的制定具有一定参考意义。

参考文献

[1] 王斌，李丽，刘臣宇，等. 边际效益分析法在航材保障经费配置中的应用 [J]. 物流技术，2009（5）.

[2] 郭峰，刘臣宇，郭星香. 基于动态规划算法的航材保障经费优化配置[J]. 价值工程，2010，29（10）：63-64.

[3] K Deb，A Pratap，S Agarwal，T Meyarivan. A Fast and Elitist Multiobjective Genetic Algorithm：NSGA-II [J]. IEEE Transactions on Evolutionary Computation，6（2）：0-197.

[4] 奉铜明，钟志华，闫晓磊，等.基于NSGA-II算法的多连杆悬架多目标优化 [J]. 汽车工程，2010，32（12）：1063-1066.

[5] 顾晨，乐秀璠. 基于NSGA-II的分布式电源优化配置 [J]. 电力系统及其自动化学报2012（04）：134-137.