建筑工程饰面砖粘结强度检验的测量不确定度分析
2020-04-08徐伟文
徐伟文
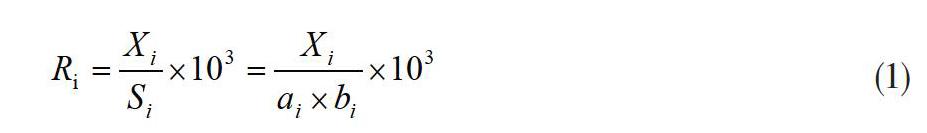


摘 要:建筑工程饰面砖粘结强度关系到人民生命财产的安全,建筑物饰面砖因粘结强度问题造成脱落伤人毁物的事故时有发生,因此建筑工程饰面砖粘结强度检验显得十分重要。依据JGJ/T 110-2017《建筑工程饰面砖粘结强度检验标准》,该文将以尺寸为95mm×45mm的饰面砖试样进行粘结强度检验,分析建筑工程饰面砖粘结强度检验的测量不确定度,供同行参考。
关键词:建筑工程饰面砖粘结强度 检验 不确定度 准确性
中图分类号:TU767 文献标识码:A 文章编号:1672-3791(2020)02(a)-0037-02
依据中华人民共和国国家计量技术规范对建筑工程饰面砖粘结强度检验中有关测量不确定度的评定进行论述,提高了测量数据的准确性。
1 检验方法
1.1 检测仪器
(1)粘结强度检测仪,最大试验拉力宜为10kN,最小分辨率单位为0.01kN,数显式粘结强度检测仪应符合现行业标准《数显式粘结强度检测仪》JG/T 507的规定。经检定合格,并在有效期内使用。
(2)钢直尺的分度值应为1mm,经检定合格,并在有效期内使用。
(3)标准块,尺寸为95mm×45mm×8mm的45号铬钢。
(4)标准块胶粘剂,粘结强度宜大于3.0MPa。
2 测量原理
按照JGJ/T 110-2017《建筑工程饰面砖粘结强度检验标准》,饰面砖截面为矩形,单个饰面砖粘结强度以试验过程峰值粘结力除以该试样的断裂面积表示,用钢直尺测量试样每对切割边的中部距离(精确到1mm)作为试验边长。每组饰面砖为3个试样,取粘结强度平均值为试验结果。检验结果具体见表1。
3 数学模型
(1)
式中,Ri为第i个试样粘结力强度(MPa),精确到0.1MPa;
Xi为第i个试样粘结力(kN),精确到0.01kN;
Si为第i个试样面积(mm2),精确至1mm2;
αi为第i个试样长边中部断面边长(mm),精确至1mm;
bi为第i个试样短边中部断面边长(mm),精确至1mm。
依据规范JJF 1059-1999《测量不确定度评定与表示》,得出:
(2)
式中,Urel(R)为合成标准不确定度;
Urel(X)为粘结力不确定度分量;
Urel(S)为试样断面边长测量不确定度分量;
Urel(r)为重复性测量影响分量。
4 测量不确定度分量
4.1 粘结力测量引入的不确定度分量Urel(X)
粘结力的测量不确定度来源于仪器校准引入的不确定度及仪器的测量不确定度。
4.1.1 仪器校准引入的测量不确定度U1rel(X)
根据检定证书LCL201803378,可知仪器校准结果扩展不确定度U=0.5%,保护因子k=2,标准不确定度为:
(3)
4.1.2 仪器的测量不确定度U2rel(X)
根据检定证书LCL201803378,数显粘结强度检测仪的最大误差为0.5%,以矩形分布估计,标准不确定度为:
=0.289% (4)
两者合成不确定度:
=0.38% (5)
4.2 试样断面长边边长a测量引入的不确定度分量Urel(α)
4.2.1 钢直尺的误差导致的不确定度U1rel(α)
钢直尺的最大允许误差为1mm,以矩形分布估计,则:
(6)
(7)
4.2.2 人员读数误差引入的不确定度U2rel(α)
钢直尺的分度值为1mm,读数误差限为1mm,可认为绝对误差值为0.5mm,以矩形分布估计,则:
(8)
(9)
两者合成不确定度:
(10)
4.3 同理可得断面短边边长b测量引入的不确定度分量Urel(b)
Urel(b)=0.645% (11)
4.4 面积的合成相对不确定度
Urel(S)=Urel(α)+Urel(b)=1.29% (12)
鉴于试样断面长边边长和短边边长测量的不确定度分量完全正相关,则面积的合成相对不确定度为
4.5 温度效应修正引入的标准不确定度
由于该实验对温度要求并不严格,而且相对于本地区常年温度约在0℃~40℃之间,符合《标准》JGJ/T 110-2017规定的实验温度条件,故忽略温度对本实验的影响。
4.6 采用A类不确定度评定,贝塞尔公式
(13)
(14)
(15)
(16)
式中:S(q)为标准差;
n为试样数量;
qk为单个强度值(MPa);
为强度平均值(MPa)。
4.7 饰面砖粘结强度的标准不确定度合成
(16)
(17)
5 擴展不确定度
取包含因子k=2,因此U=2Uc=0.06MPa。
6 测量不确定度报告
饰面砖粘结强度R=(0.7±0.06)MPa。其中扩展不确定度U=0.06,是由标准不确定度Uc=0.03,乘以包含因子k=2得出的。
参考文献
[1] JG/T 110-2017,建筑工程饰面砖粘结强度检验标准[S]. 北京:中国建筑工业出版社,2017.
[2] JJF 1059-1999,测量不确定度的评定与表示[S].北京:中国计量出版社,1999.
[3] 郑党儿.简明测量不确定度评定方法与实例[M].北京:中国计量出版社,2005:13-18,59-67.
[4] 倪育才.实用测量不确定度评定[M].北京:中国计量出版社,2007:17-31,70-71,82.
