二维局部异常体与起伏地形复杂电磁场的畸变矩阵性质研究

刘子杰， 胡艳芳， 汤井田， 原 源, 邹明亮， 董湘龙

(1.核工业二三〇研究所，长沙 410011；2.有色资源与地质灾害探查湖南省重点实验室，长沙 410083；3.有色金属成矿预测与地质环境监测教育部重点实验室(中南大学)，长沙 410083；4.中南大学 地球科学与信息物理学院，长沙 410083；5.东华理工大学 地球物理与测控技术学院， 南昌 330013)

0 引言

20世纪50年代，在前苏联学者吉洪诺夫和法国学者卡尼亚[1-2]经典著作的基础上形成了大地电磁测深法(MT)，并逐步得到了广泛的应用。上世纪以来我国的大地电磁工作已经取得了很大的进步，并取得了大量的成果[3]。在野外实际工作中，对于浅地表局部异常体与地形起伏所造成的局部畸变的研究一直是大地电磁学者关注的研究课题[4-8]。电磁场局部畸变的产生是由于局部异常体和起伏地形的存在，会在其表面产生积累电荷，这在一定程度上将对真实的区域响应造成影响，需要我们在后续的数据处理过程中加以分辨。伴随着阻抗张量分解技术的发展，对电磁场畸变有了深入地研究。阻抗张量分解(Bahr、GB分解等)，可以用来减小浅地表局部异常体和地形起伏所导致的电场畸变的影响，进而获得更符合区域模型的定性参数，可以给反演提供更合理的反演方案、初始模型、约束模型或判断反演结果好坏的标准，这也是阻抗张量分解技术产生的原因和背景。在目前利用阻抗张量分解技术求解畸变矩阵的方法中，一般情况下假设区域构造为二维，而浅地表的局部异常体为三维，当浅地表的局部异常体的尺度远远小于趋肤深度时，在此情况下局部异常体附近的测点会受到严重的畸变，称之为“局部畸变”[9]。从上世纪70年代开始，国内、外许多学者陆续对电磁场的局部畸变进行了相关研究。Berdichevsky[10]在理论上研究了水平电性差异所引起的畸变问题，提出了感应型畸变和电流型畸变；Larsen[11]研究了3D/1D地质模型的畸变规律；Zhang[12-13]研究了2D/2D模型下局部异常体所造成的电场畸变影响。进入80年代末期和90年代，已经有许多学者对畸变矩阵形式和求解方法进行了比较深入地研究。Bahr[14-15]、Groom等[16-17]在忽略磁场畸变的条件下，对电场畸变矩阵的形式和消除进行了研究，提出了Bahr分解和GB分解等阻抗张量分解方法；随后Chave和Smith[18-21]在理论上推导了电磁场全畸变模型，并对近地表3D局部异常体引起电磁场畸变的物理原理进行了研究；Agarwal等[22]同时考虑了电磁场畸变，运用数值模拟的方法对3D/2D模型，对浅地表的3D局部异常体所造成的电磁场畸变进行了研究，并与前人的研究结果进行了相关对比，讨论了其影响规律。在国内，许多研究学者利用阻抗张量分解、阻抗张量旋转不变量、相位张量等手段进行局部畸变的消除，并将其运用到实测数据的处理解释中[23-26]。

在目前进行电磁场畸变研究和实际的数据处理中，一般情况下需要假设以下几个条件，即频率足够低，此条件下可忽略方程位移电流项；畸变矩阵为实数，进而降低方程未知数；且畸变影响与频率无关。在前人的研究工作中，对于这些假设条件的适用性及其适用条件缺少相关的论证工作，基于此笔者通过正演模拟的方法简单讨论在二维介质条件下局部异常体和起伏地形对电磁场畸变矩阵的影响规律以及上述假设的适用性。

1 局部畸变基本理论

在实际的野外工作中，MT方法获得的是观测张量阻抗信息，利用阻抗张量分解技术可以减小由电磁场畸变引起的观测误差，获得更为准确的区域构造阻抗。从阻抗分解的角度来看，诸如Bahr分解、GB分解、相位张量分解等等，都可以在一定程度上降低局部畸变的影响。目前应用比较广泛的是GB分解法，该方法是Groom和Bailey[16-17]于20世纪90提出了一种新的阻抗张量分解方法。GB分解是针对三维/二维模型的大地电磁阻抗张量提出的一种分解方法，它将畸变矩阵理解为对区域电场的旋转与放大，在将畸变矩阵与区域阻抗张量分离开来的同时在畸变矩阵中求解出不同的畸变因子。

针对3D/2D模型，若只考虑电场畸变的条件下，区域构造主轴坐标系顺时针旋转θ角到测量坐标系中，观测阻抗Zm为：

Zm=R(θ)DZ2DRT(θ)

(1)

式中：Z2D是走向坐标系中的区域二维构造阻抗张量；D为2×2的畸变矩阵。

为了对畸变矩阵D作因子分解，因此引入单位矩阵I和泡利自旋转矩阵阵变换：

(2)

任何二阶矩阵都可以表示各式的线性组合。因此观测阻抗张量Zm可以表示为：

(3)

这里的分解系数定义为：

α0=Zm xx+Zm xy

α1=Zm xy+Zm yx

α2=Zm xy-Zm yx

α3=Zm xx-Zm xy

(4)

Groom和Bailey认为，D=gTSA，此中g为标量，为测点增益；剪切矩阵、扭曲矩阵、各向异性矩阵依次表示为：

S=n1(I+e∑1)

T=n2(I+t∑2)

A=n3(I+s∑3)

(5)

系数n为归一化因子；e、t、s分别为剪切因子、扭曲因子和各向异性因子。因此畸变矩阵D可以表示为：

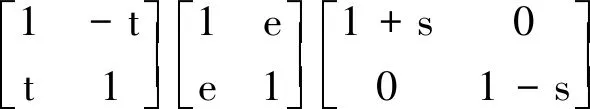
(6)

由式(6)可以看出，增益因子部分和各向异性矩阵A与区域二维构造阻抗具有相同的形式，为畸变矩阵D的不可确定部分，因此可以将其并入区域二维构造阻抗中。因此观测阻抗可以表示为：

(7)

式(7)中：

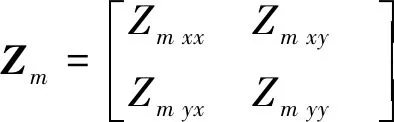
从局部畸变的物理意义上来看，野外观测阻抗的畸变其本质就是由于观测电磁场受到电性不均匀体的影响所致。根据J. Torquil Smith[20]对电磁场畸变理论的研究可以看出，在同时考虑电场和磁场畸变的条件下，区域电磁场和总场之间存在如下关系：

Em=Er+Eg

(8)

Hm=Hr+Hg

(9)

式中：角标m表示观测总场；角标r表示区域电磁场；角标g表示由局部异常体或地形起伏引起的畸变电磁场。

对于畸变电场可以表示为：

Em=DEr

(10)

由于畸变磁场是由畸变电流引起的，畸变磁场和区域电场之间具有相位相同的特点，因此畸变磁场是作用在区域水平电场之上，表示对水平磁场的电流沟道效应，可以表示为：

Bg=CEr

(11)

矩阵D称之为电场畸变矩阵；矩阵C称之为磁场畸变矩阵。畸变矩阵的实部是由静电场引起的，而虚部是由感应场导致的。根据阻抗张量定义：

Em=ZmHm

(12)

因此根据上述方程可以得到在全畸变条件下观测阻抗和区域阻抗之间的关系为：

Zm=DZr-Zm(CZr)

(13)

如果在只考虑电场畸变而忽略磁场畸变的条件下，即C=0，则式(13)可以表示为：

Zm=DZr

(14)

在目前MT实测数据的处理解释中，二维反演仍然是应用比较广泛的方法。因此研究2D/1D模型下畸变矩阵的影响规律，即浅地表的局部异常体为2D构造，区域构造为一维层状介质。首先在畸变矩阵的求解中，将不存在局部异常体的层状介质模型的正演结果作为区域构造信息，将存在局部异常体的结果作为受到畸变之后的观测数据。通过改变局部异常体的电阻率、相对介电常数和相对磁导率等物理参数来研究其畸变矩阵的影响规律；此外，在不存在异常体的情况下，通过加入地形起伏来研究其对电磁场产生的畸变影响。在此情况下，可以利用方程(10)来计算电场畸变矩阵D，利用公式(15)来获得磁场畸变矩阵C，即：

Bm-Br=CEr

(15)

在2D正演程序中，我们计算了TE和TM两种模式下的电磁场数据，根据式(10)可以得到观测电场和区域电场之间的关系：

(16)

将式(16)按元素展开可以得到：

(17)

由式(17)可知此时由于电场非对角元素为0，因此在畸变矩阵的求解结果中只存在畸变矩阵的对角元素，也就是说D12和D21均为0；D11和D22分别表示TE模式和TM模式中的电场畸变强度。在无畸变情况下，D11和D22均为1。当D11>1时，表示电场畸变引起TE模式下的观测电场值偏大，反之则使观测电场值偏小；对D22而言，也是如此。

对于磁场畸变矩阵C而言，根据方程(15)可知：

(18)

展开分式形式为：

(19)

图1 2D/1D正演模型示意图

图2 不同电阻率条件下局部异常体6号测点电场畸变矩阵实虚部曲线及视电阻率相位曲线

此时畸变矩阵中只存在畸变矩阵的非对角元素，即C11和C22均为“0”；C12和C21分别表示TM模式和TE模式中的磁场畸变程度。在无畸变情况下，C12和C21均为“0”。

2 局部异常体模型

笔者设计了如图1所示层状介质模型(不存在局部异常体时表示为模型1)，区域构造为二层模型，第一层电阻率为100 Ω·m，厚度为3 km；第二层电阻率设置为1 000 Ω·m，厚度无限大；在地表设置一个厚度为10 m、长度为500 m局部异常体(地表出露的电性不均匀体)；点O为原点，地表测点的点距设置为100 m，测点编号为1～11，测点剖面为-500 m～500 m；频率设置采用了10 000 Hz～0.01 Hz之间等对数间隔的41个频点。正演程序利用基于非结构化网格的带地形的2D大地电磁正演程序进行计算[27]。

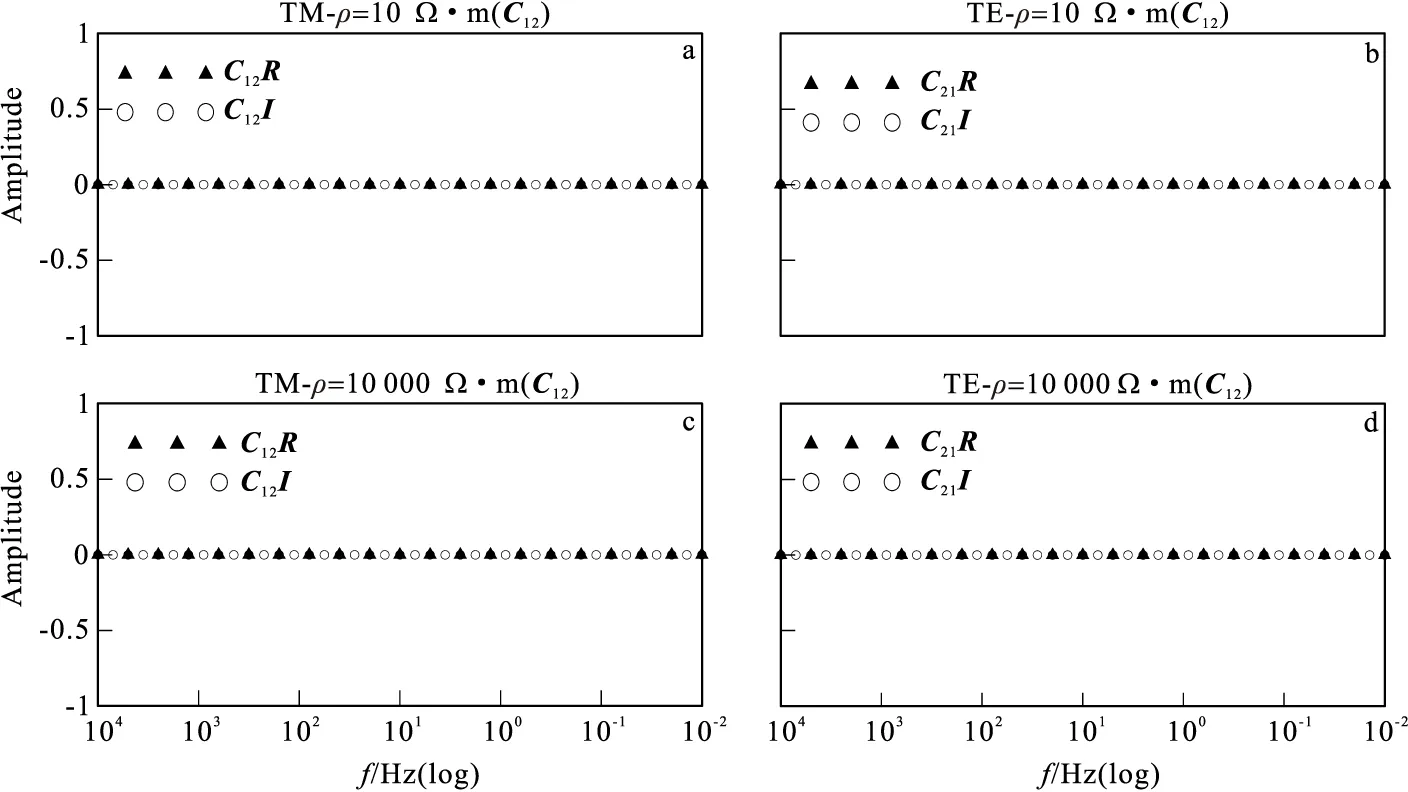
图3 不同电阻率条件下局部异常体6号测点磁场畸变矩阵实虚部曲线

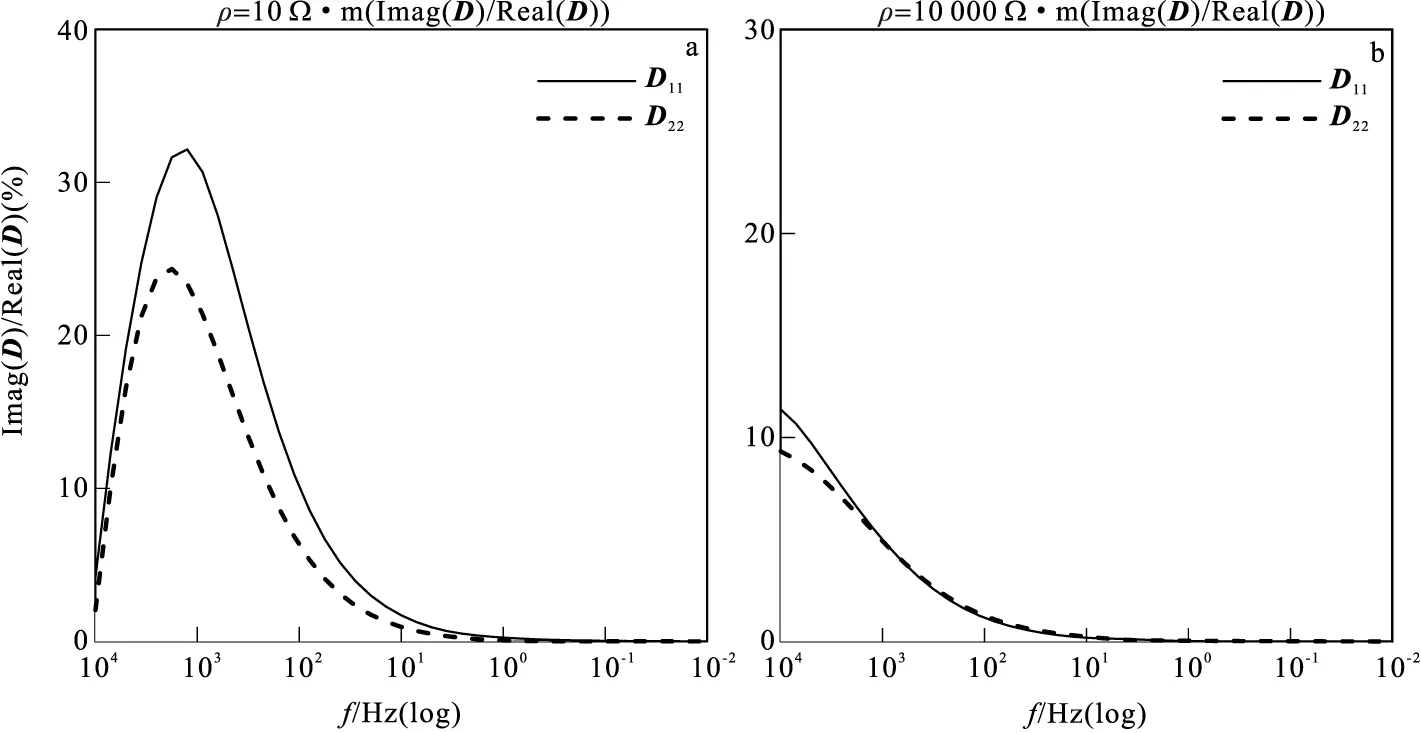
图4 不同电阻率条件下局部异常体6号测点电场畸变矩阵实虚部比值曲线

在上述模型的基础上设置局部异常体的电阻率值分别为10 Ω·m的低阻异常体(模型2)和10 000 Ω·m的高阻异常体(模型3)，通过正演计算求得电场畸变矩阵D和磁场畸变矩阵C的实虚部数值。

图2为低阻和高阻局部异常体模型下6号测点的电场畸变矩阵D实虚部曲线图以及畸变前后视电阻率和相位曲线。图3为不同电阻率条件下局部异常体6号测点磁场畸变矩阵C实虚部曲线。

由图2可以看出，对于低阻异常体而言，TE模式在10 000 Hz～56 Hz电场受到的畸变程度较大，将导致电场值偏小，进而导致视电阻率在高频段偏低，而相位受畸变的程度较视电阻率要弱；在低于56 Hz时其畸变因子实部几乎趋近于“1”，虚部趋近于“0”，受到的畸变程度非常微弱；在TM模式可以看出在整个频段D22的实部都小于“1”，说明电场畸变存在于全频段，高频段受畸变程度要大于低频段，视电阻率整体偏低，这是由于TM模式的电场需要穿过电性分界面将在界面两侧产生感应电荷，其形成的二次电场与一次场相互叠加，会造成一次场畸变更为严重；对于高阻局部异常体来说，同样TE模式在高频段使电场畸变的程度较大，其实部值在10 000 Hz～223 Hz高频段数值偏大造成电场值增大，电阻率偏大，在低频段其影响程度几乎为零；在TM模式，在整个频段受到了电场畸变的影响，高频受影响程度仍然大于低频，两种模式下电场畸变因子虚部的值非常小；同时高阻局部异常体对相位的影响几乎可以忽略。低阻局部异常体所造成的电场畸变要比高阻局部异常体严重的多。

图5 低阻和高阻局部异常体电场畸变矩阵拟断面图

对存在电阻率差异的局部异常体所造成的磁场畸变来说，由图3可以看出，在全频段磁场畸变的程度相当微弱，相对于电场畸变而言可以忽略，符合前面的假设条件。

由上述分析可知，在相比于电场畸变来说磁场畸变相当微弱，因此可以忽略，对于电场畸变矩阵需分析其实虚部比值问题，检验其是否符合实数的假设。图4为低阻异常体模型和高阻异常体模型6号测点电场畸变矩阵的虚部与实部的比值曲线，由图4可以看出：在低阻模型中，在高频段TE模式10 000 Hz～56 Hz与TM模式10 000 Hz～316 Hz，其虚部相对于实部的比例达到10%以上，最大值可达到33%，在该频段畸变矩阵不符合为实数的假设，其畸变矩阵变得更为复杂；在低频段其虚部比例相对减小，频率越低所占比例越小，可以认为畸变矩阵D为实数。而在高阻模型中，在整个频段虚部所占比例基本小于10%(除了D11高频两个频点之外)，高频段相对低频段要大，基本上符合畸变矩阵D为实数的假设。

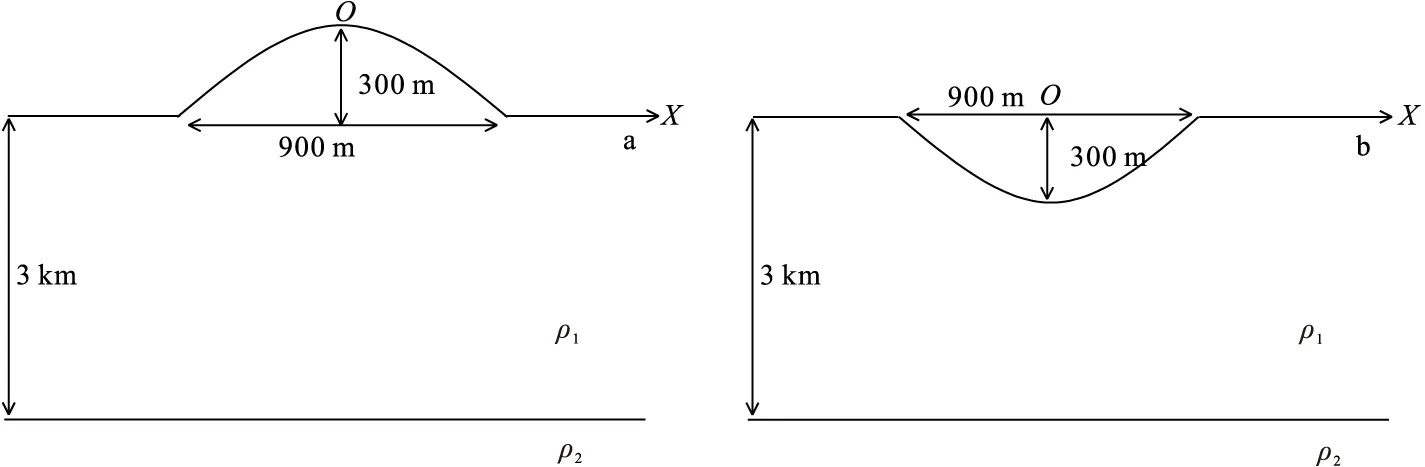
图6 起伏地形正演模型

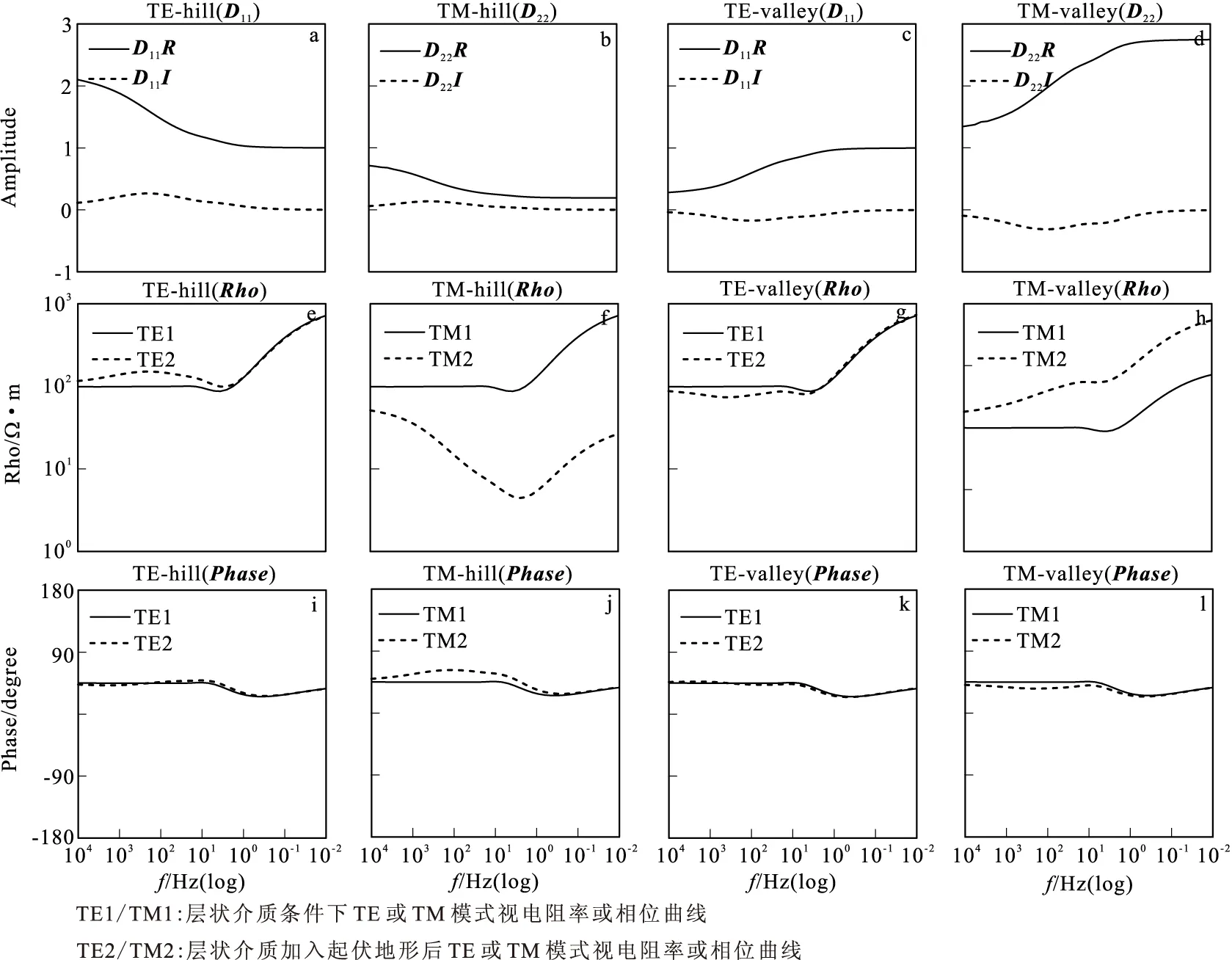
图7 起伏地形模型6号测点电磁场畸变矩阵实虚部曲线及视电阻率相位曲线

通过对单点畸变矩阵曲线分析可知，局部异常体主要影响MT/AMT的高频数据，使其电场发生畸变，而在低频段其影响程度相对较弱。图5为电阻率差异的局部异常体模型造成电场畸变矩阵D的拟断面图，横坐标间距为100 m。由图5可以看出，整个剖面基本符合畸变程度由高频向低频变弱的规律，而高阻局部异常体的影响程度要比低阻异常体弱；在TM模式，无论高阻还是低阻异常体在测点200和300附近畸变因子相对于其他测点都出现了比较明显的偏差，这个是由于异常体边界的积累电荷所引起的。

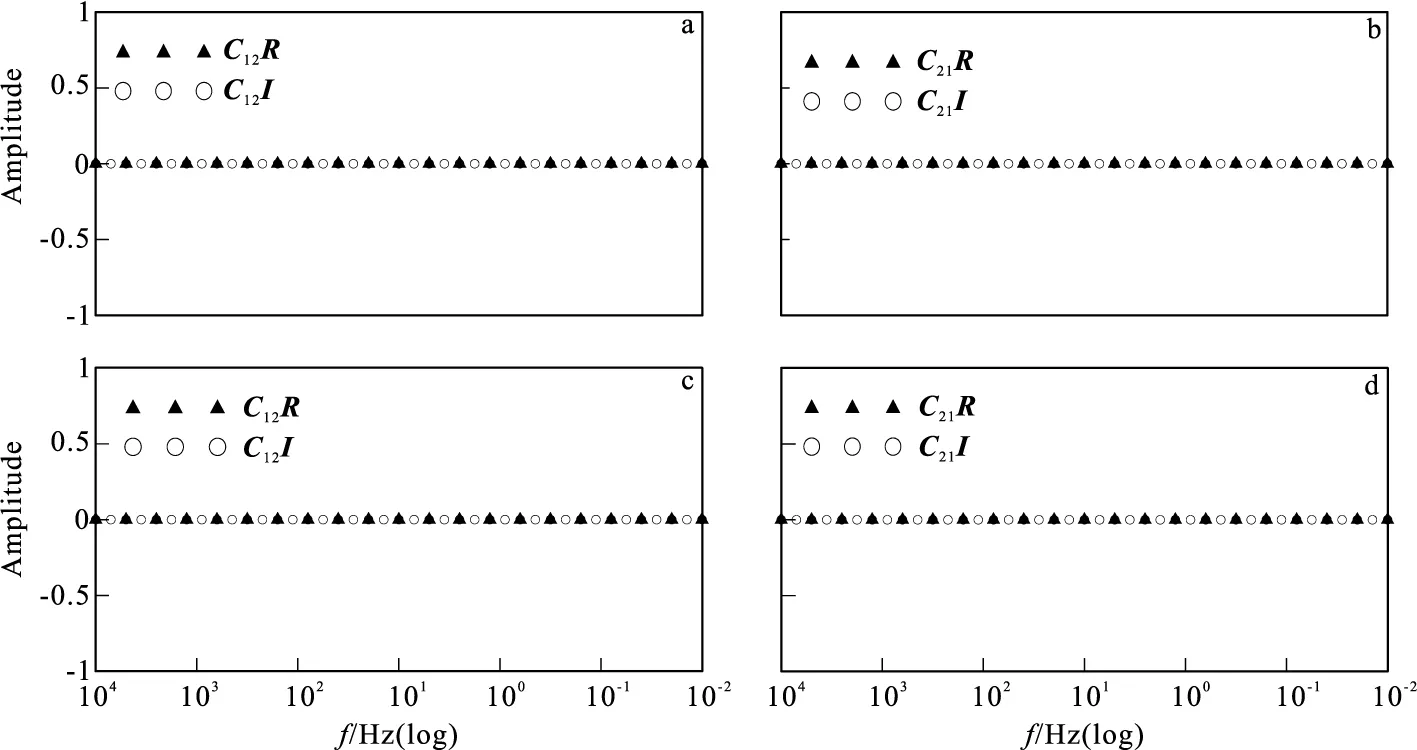
图8 起伏地形模型6号测点磁场畸变矩阵实虚部曲线

图9 起伏地形模型6号测点畸变矩阵实虚部比值曲线

3 起伏地形模型

地形的起伏变化，可以由山峰和山谷两个基本地形单元构成，任意复杂的地形可以是这两种基本单元的组合。基于图1的模型，同样以去除局部异常体的层状介质模型结果为区域响应，在其基础上增加了地形进行正演计算，用以研究地形对电磁场畸变的影响。设计地形为以余弦函数变化的山峰模型和山谷模型，其高度和深度均为300 m，地形水平长度为900 m，设置11个测点，如图6(模型4)所示。图7为地形起伏模型4号测点(测点布置见图1)电磁场畸变矩阵实虚部曲线及视电阻率相位曲线，图8为其磁场畸变矩阵实虚部曲线。

根据图7可以得出，在山峰和山谷模型下，其TE模式的电场畸变矩阵在高频段(10 000 Hz～1 Hz)受畸变影响严重，山峰模型使其电场值偏大，电阻率在高频段偏大，低谷模型使其电场值偏小，进而导致电阻率值偏低，而在低频段(<1 Hz)其受影响的程度相对来说十分微弱，实部趋近于“1”，虚部趋近于“0”；在TM模式，其受畸变的程度要远大于TE模式，而且呈现畸变程度由高频向低频增大的趋势，也就是说在低频段受到的畸变更为严重，山峰模型使其电场值降低、视电阻率降低而山谷模型使其电场值增大、视电阻率增大，且山峰模型的影响相比于山谷模型的影响要大得多。上述结论的进一步解释为对于山峰地形，在左边分界面上TM模式的水平一次场等同于由高阻一侧进入低阻一侧，在界面上会累积负电荷，而在右边分界面上由低阻一侧进入到高阻一侧会累积正电荷，这样在两侧分界面上由积累电荷产生的二次场与一次场方向相反，导致总场减小。同样的道理，会使山谷TM模式的观测的总场值增大。

图8为山峰和山谷模型下磁场畸变矩阵元素的实虚部曲线，从图8可以看出，同具有电阻率差异的局部异常体相同，地形起伏所造成的磁场畸变十分微弱，可以忽略。

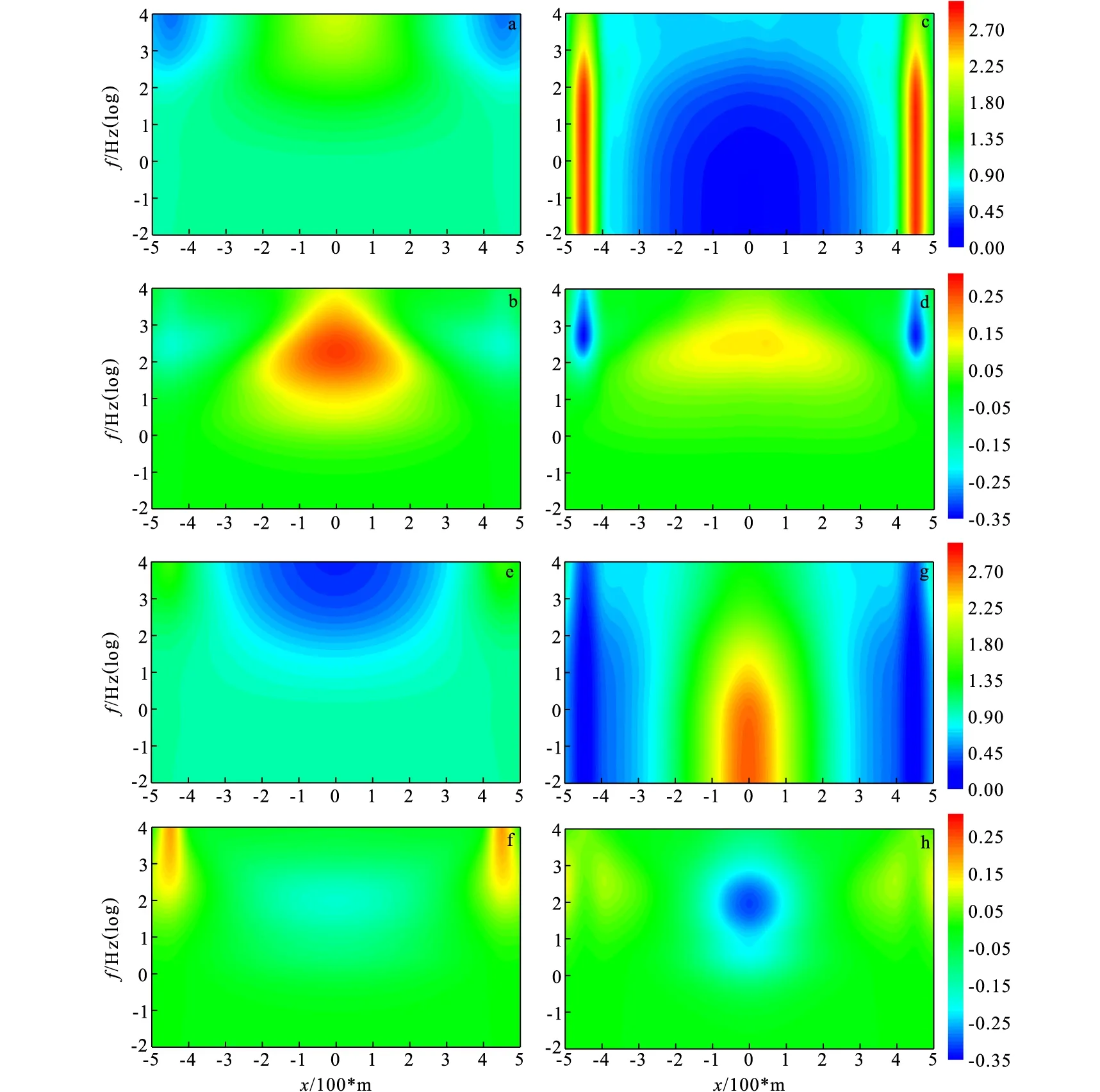
图10 起伏地形模型电场畸变矩阵拟断面图

图9为山峰和山谷模型4号测点电场畸变因子的虚部与实部比值曲线。对于山峰模型而言，两种模式下的畸变矩阵在中高频段(TE模式1 258 Hz～5 Hz，TM模式5 011 Hz～1.25 Hz)其虚部所占的比值都超过10%，且二者都在112 Hz附近达到最大值分别为17%和31%，在此频段内畸变矩阵虚部相对较大，矩阵元素复杂，不符合实数的假设；对于山谷模型，其虚部比值在10 000 Hz～3.5 Hz(TE模式)和1 778 Hz～14.1 Hz(TM模式)频段超过实部的10%，在223 Hz时达到最大值分别为33%和16.6%，因此在该频段内电场畸变矩阵相对复杂，但其频带要比山峰模型较窄。

由图10可以看出同单点畸变曲线一样，地形对TE模式的影响较小，其浅部即高频段数据受畸变程度相对于低频较大；对TM模式而言，由于地形导致的电场畸变要相对TE模式大，几乎影响数据的全频段，且呈现由高频到低频影响增大的趋势；在±450 m附近正好处于地形的边缘，它和地形上方的数据的畸变规律相反，这是由于地形边界所引起的。

4 讨论与结论

通过正演模拟的方法，研究了存在电性差异的浅地表局部异常体以及地形起伏对电磁场畸变的影响，对于类似模型取得了以下三点认识：

1)对于浅地表具有电阻率差异的局部异常体，低阻异常体对电场造成的畸变要比高阻异常体严重，二者畸变程度随着频率的降低而减小，到低频时几乎不存在电场畸变；此外低阻异常体模型的高频段畸变矩阵的虚部不可以忽略，且与频率相关，在低频段可以看作为一个实数矩阵。

2)对于存在地形起伏的模型数据来说，TM模式受到的畸变程度要比TE模式大得多；山峰模型会导致TE模式的电场观测值增大、视电阻率偏大，TM模式的电场观测值降低、视电阻率偏小，山谷模型则与之相反；在高频段TM模式的畸变矩阵不能假设为实数，其畸变矩阵变得更为复杂，且与频率相关。

3)通过研究可知，对于高频数据来说浅地表局部异常体和地形所产生的电场畸变矩阵较为复杂，但相位数据受到的畸变影响较小；在目前的阻抗张量分解过程中无法完全求解各种畸变参数，因此在实际的数据处理中可以考虑利用相位数据进行视电阻率校正，或者采用相位张量分解技术获得较为准确的区域构造阻抗信息。