不止于“实验与猜想”，也需要“逻辑与证明”——例谈数学推理能力培养的几种方法

□金秀叶

正如史宁中教授指出的那样，推理能力的培养对于学生数学学习和综合素养的发展都有着重要的作用。《义务教育数学课程标准（2011 年版）》把推理作为十大核心概念之一，它实际上是数学学科的关键能力之一。推理教学的目的是要教给学生深层次的数学道理，最终让学生感悟数学思想，掌握基本的推理方法，逐步学会用数学的方法思考和解决问题。

推理一般包括合情推理和演绎推理。在解决问题的过程中，两种推理功能不同，相辅相成：合情推理用于探索思路，发现结论；演绎推理用于证明结论。但在实际教学中，教师一般偏重于通过实验与猜想等方法来发展合情推理，而对于需借助逻辑与证明等方式来彰显的演绎推理就不那么重视。实际上，这两种推理能力的培养不仅都需要加以重视，而且也是可能的。曹培英老师曾提出：“演绎推理不是中学几何的专利。小学数学有许多尚待发掘的演绎推理。”本文从人教版六年级下册《比例的基本性质》一课的教学实践出发，就此问题作探讨。

一、“举例—猜想—验证”的“不完全归纳”教学现状

综观人教版、北师大版、苏教版等教材，对于“比例的基本性质”一课，整个教学过程只应用了不完全归纳法。学生往往认为举例验证对了，或是举不出反例了，猜想就对了，我们的课堂一般也仅满足于此。

人教版

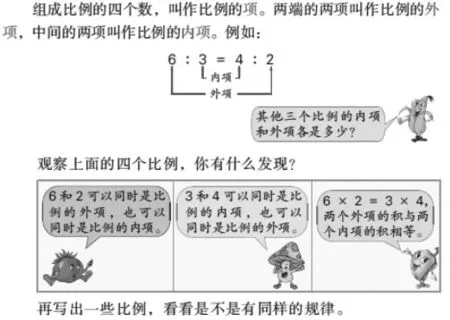
苏教版

在我们的教学中，一般都是经历“举例—猜想—验证”这样的环节，仅此而已。教材这样编排，教师照此教学。但这样的教学现状，笔者觉得有如下不足。

（1）止于不完全归纳，未能深挖本质。数学思维是一种表达特定推理过程的严谨方法，这种通过不完全归纳得出的结论，会削弱知识的逻辑联系，从而影响理解的深度。

（2）止于零散的学习，未能实现整合。生本学材的实验稿将“整理与复习”调整为“复习与关联”，目的就是期待教师重视知识之间的整合与联系。学生在一节课中能否得到能力的增长，将来又能否用联系的眼光来看待新的数学问题，是与教师平时的教学行为息息相关的。

（3）止于单一的路径，未能呈现多样。推理教学可以有多种可能，归纳推理只是其中的一种路径。放眼看，这项内容可以联系比的基本性质、等式的性质、代数的思想、图形论证等形式加以证明。

如果只应用不完全归纳法，其实就停留在“知其然”；只有讨论“为什么”，找出必然联系，那才是“知其所以然”。事实上，我们有必要去探究这个知识到底是怎么来的，为什么会是这样。

二、走向“演绎推理”的可能性教学尝试

研究比例的基本性质背后的秘密，采用完全归纳法教学合适吗？笔者认为合适与否的关键在于是否给学生搭建了“够得着”的“脚手架”，而答案应该是肯定的。

（一）透过已知性质，推出未知

在初步发现比例的两个外项之积等于内项之积后，学生起疑：为什么比例的外项之积会等于内项之积呢？是不是所有的比例都有这样的规律？通过借助已有知识，串联起某些知识之间的内部联系，对猜想的结论进行推理证明，促进学生的深度理解。

（1）利用比的基本性质。学生在研究“为什么两个外项之积等于两个内项之积”时，展开如下交流。

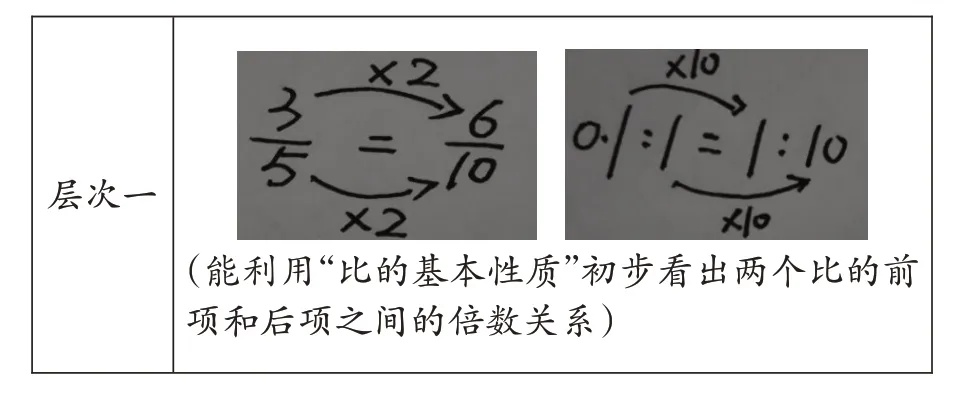
层次一（能利用“比的基本性质”初步看出两个比的前项和后项之间的倍数关系）

层次二层次三images/BZ_25_448_343_1179_565.png（能看出两积中“6”和“10”的“前世”，初步感知两个外项积等于两个内项积背后的秘密）images/BZ_25_448_777_1185_940.png（能清晰地找到规律，并说明其中的道理）

（二）利用代数方法，推出未知

三、同步走向“逻辑与证明”推理能力培养的广阔空间

强化学生的推理能力，不仅要着眼于眼前，还要看到与未来的更多联系，不仅不能简单止步于依靠“猜想与验证”对合情推理的培养，更可采用“逻辑与证明”等方式推进学生演绎推理能力的提升。事实上，在我们的教材中蕴含着很多有待挖掘的材料。那么如何基于教材，提升学生的推理能力呢？

（一）强化说理，学习逻辑化

【例1】角的度量。（人教版四年级上册P44）

从四年级测量验证、观察验证到推理论证，再到六年级下册初步感受运用一些“公理”（如等式的性质）进行数学推理。让学生体会到仅凭观察其实是不够的，要结合问题展开适当的说理，还要有一定的逻辑，且在不同的年级渗透不同的教学目标。

（二）联系整合，促进结构化

【例2】面积推导。（人教版五年级上册P103）

从学习平行四边形的面积，到学习三角形、梯形的面积，这些图形面积计算方法的习得同样离不开推理。放眼看，其实就是将新的图形转化成已经学过的图形，以此加深对几何知识的整体理解，并不断促进知识的结构化。这些方法不只是简单地局限于合情推理，同时也有不少演绎推理的成分在其中。

合情推理强调从已有事实出发，凭借经验和直觉，通过归纳和类比等推断某些结果，而演绎推理是从已有的事实（包括定义、公理、定理等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则证明和计算。在解决问题的过程中，两种推理功能不同，相辅相成。人民教育出版社王永春老师在《小学数学总复习要点简析——以“推理思想和运算能力培养”为例》一文中指出：“为了中小学衔接，演绎推理在小学数学中可适当加强。教学中经常启发学生思考一些问题：为什么这样算？怎样得出的结论？”

实践证明，推理真的不只是中学生的专属，只要“有理有据”，小学生也可以做出精彩的论证。“数学”不仅需要“实验”与“猜想”，更需要逻辑与证明的参与，让学生知道“是什么”，更明了“为什么”，从而学会“前联后延”，真正培养学生的推理能力。