砾砂与混凝土管界面剪切力学特性试验
2020-04-08李天亮韩健勇
赵 文, 李天亮, 韩健勇, 程 诚
(1.东北大学 资源与土木工程学院, 辽宁 沈阳 110819; 2. 山东建筑大学 土木工程学院, 山东 济南 250014)
随着城市建设的高速发展,顶管施工技术在地下工程中得到了广泛的应用.在顶管工程中,对于混凝土管顶进的界面研究多采用模型箱或剪切试验[1-3]进行宏观力学研究,且许多学者只得到了其顶进时的界面摩擦系数.对于顶进过程中界面的屈服准则、切向和法向变形规律以及界面剪切破坏演化机制等关键问题尚未得到深入研究.
在界面力学特性的研究中,直剪试验由于其操作方法简便易行、结果直观准确并且可以详细地记录接触面上的相对位移、剪应力及法向位移等优点,被广泛应用.以往直剪试验[4-8]研究成果,往往由于传统的直剪容器以及试验测试方法的局限性,对界面剪切过程中细观破坏机制研究不足.本文采用数字图像相关[9-10](digital image correlation,DIC)技术研究土与结构物剪切破坏的特性,该技术通过比较物体表面变形前后的数字图像,直接获取位移和应变,可以从多方面获得土体细观变化信息.
综上所述,砾砂-混凝土管界面的剪切力学特性和细观破坏机理仍需进一步研究.本文将通过可视化界面直剪试验,对常法向应力条件下土样相对密实度影响的砾砂与混凝土界面剪切力学特性的规律展开分析,并对界面剪切过程中的土样位移场进行深入研究,以期对砾砂层顶管工程的顶力计算及其引起的环境效应提供理论依据.
1 接触面试验
1.1 试验材料
试验采用沈阳地区典型砂土,取自沈阳市区南部地铁9号线曹仲站施工现场,根据颗粒级配曲线判断为砾砂,土样具体参数见表1,限于篇幅,此部分试验不做详细介绍.混凝土采用顶管常用标号:C40.

表1 砾砂的基本物理力学参数
1.2 试验仪器
本文采用300 kN双轴伺服剪切试验机,该试验机具有精密的量测设备和伺服液压控制系统,通过控制系统可实现水平和竖直两个方向的试验力加载和位移加载.
本试验自主研制了适用于数字图像相关测量技术的可视化直剪盒,见图1.为观察剪切过程中的砾砂土样扰动变化,剪切盒采用有机玻璃材料(PMMA)制作,直剪盒上盒内部尺寸为100 mm×100 mm,外部尺寸为200 mm×160 mm,高50 mm.上盒上方设置加载垫板,用于承受剪切仪法向加压.直剪盒下盒内部尺寸为100 mm×140 mm,外部尺寸为200 mm×160 mm,保证试样在剪切过程中剪切界面始终保持在砾砂与混凝土之间,增加了土与结构间的滑移范围,较传统直剪仪更贴近实际工程情况.在上下盒之间涂抹工业用凡士林润滑脂,通过空剪切盒剪切测试,发现上下盒之间的剪切力几乎为0,故其摩擦阻力可忽略不计.以上说明该剪切盒可配合数字图像相关测量技术研究剪切界面的力学特性.
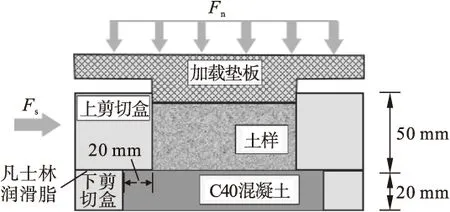
图1 可视化直剪盒
1.3 试验方案
结合沈阳地区原状土层状态,本文选取Dr=0.4,Dr=0.6,Dr=0.8三种具有代表性的相对密实度作为试验变量,共设计了15组试验,试样详细参数见表2.

表2 砾砂-混凝土直剪试验(Dr=0.4,0.6,0.8)
界面剪切试验具体步骤如下:
1)剪切盒填装:在剪切盒下盒浇筑配置好的C40混凝土,利用表面平整的纸板进行压面,控制其表面的粗糙度接近实际管体,分五层均匀铺设砾砂,通过控制每层高度确保其相对密实度,此后放置加载垫板,置于剪切台.
2)加载剪切:按目标荷载进行法向加压,设置水平剪切速率为1 mm/min[11],水平剪切位移每间隔0.5 mm用高像素照相设备进行拍照记录,见图2.

图2 剪切试验装置
2 试验结果分析
2.1 剪应力与剪切位移
根据不同相对密实度情况下的界面剪切试验,可得常法向应力条件下砾砂-混凝土接触面剪应力-剪切位移曲线,见图3.抗剪强度的取值参照《土工试验方法标准》GB/T 50123—1999,规定应力应变曲线上0~4 mm范围内的峰值剪应力为试样的抗剪强度,若剪应力无峰值,取剪切位移为4 mm对应的剪应力为抗剪强度.

图3 剪应力-剪切位移曲线
由图3可知,在常法向应力条件下,剪应力与剪切位移的变化规律呈现明显的非线性.在剪切初始阶段,剪切位移较小,剪应力-剪切位移曲线近似线性,其剪切模量随法向应力的增长而增大.而当剪切位移继续增加时,不同法向应力作用下的应力应变曲线出现明显差异.
为了讨论法向应力对剪切界面达到抗剪强度时所需位移的影响,以试样RD-A3(Dr=0.8)为例,将图3中法向应力影响下的峰值应力剪切位移进行整理,见表3.

表3 峰值剪应力对应剪切位移值(RD-A3)
由表3可知,峰值应力剪切位移随法向应力的增大而增加,分析原因为法向应力将影响土体颗粒在剪切过程中的运动状态.接触面受剪切作用时,土颗粒之间产生相互跨越、翻滚等行为,法向应力较小时,土颗粒之间的相对位置容易改变,能够在很短的时间内达到相对稳定状态,而法向应力较大时,土体被压实,法向应力限制了土颗粒之间的相对移动,因此需要较大的剪切位移才能达到较稳定的状态.
2.2 界面抗剪强度分析
图4所示为各接触面抗剪强度与法向应力关系曲线.当法向应力为50 kPa时,抗剪强度受相对密实度的影响不规律,分析原因为法向应力较小时,界面处的土颗粒与混凝土在剪切过程中受到的法向约束较小,不同相对密实度情况下的土颗粒均易发生跨越、滚动等行为,故抗剪强度变化差异不大.当δ≥100 kPa时,法向应力一定的情况下,接触面的抗剪强度随试样相对密实度的增大而增大,但二者并非线性的关系,结合图3可知,相对密实度对后期残余强度的影响不显著.密实度一定的情况下,法向应力对接触面的抗剪强度影响显著.以试样RD-A1为例,不同法向应力对应的界面抗剪强度见表4.由表可知,抗剪强度随法向应力增加呈线性增大,法向应力每增长50 kPa,抗剪强度平均增加27 kPa.

图4 抗剪强度与法向应力

表4 RD-A1抗剪强度(Dr=0.4)
根据图4可知,界面抗剪强度与摩擦系数随相对密实度的增大而增大,即顶管与土体间的摩擦系数随着土体相对密实度的增大而增加,在Dr=0.4~0.8时,摩擦系数在0.538到0.632之间变化,Dr=0.8时的顶进阻力较Dr=0.4时增大了17.5%;界面的摩擦角同样随相对密实度的增大而线性增长,经线性拟合得到砾砂与混凝土接触面的摩擦角随相对密实度变化的计算公式:φ=24.167+10Dr,故相对密实度每增长0.2,摩擦角平均增大2°.
2.3 界面剪切应力应变曲线特征
为了探究土样相对密实度和法向应力对接触面剪切应力曲线的影响规律,本文引入了“强残比”的概念,令强残比为γ=τm/τg.式中,τm和τg分别为接触面抗剪强度和残余剪切强度(即剪应力趋于稳定时的数值).并且γ>1,表明应力应变曲线发生软化现象;γ<1时,应力应变曲线发生硬化现象;γ=1则表明应力应变曲线接近理想弹塑性.强残比与法向应力的关系见图5.
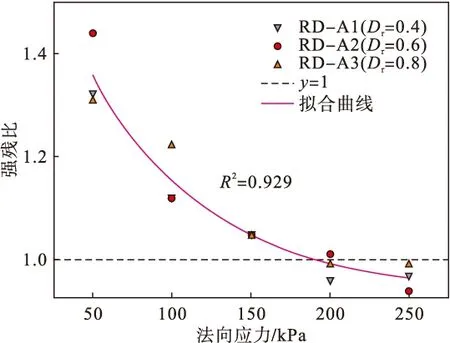
图5 界面软硬化特性
由图5可知,当法向应力δ=50 kPa,Dr=0.4,0.6,0.8时,γ分别为1.32,1.44,1.31.砾砂与混凝土接触面的强残比随法向应力的增大逐渐减小,即砾砂与混凝土接触面的剪应力-剪切位移曲线软化趋势随法向应力的增大逐渐减弱,硬化趋势逐渐增强.
为了探究相对密实度对接触界面应力应变曲线特征的影响,对比试样RD-A1和RD-A3的强残比,发现相对密实度大时的界面应变软化特性较相对密实度小时更易发生.验证了陆勇等[12]提出的同一粗糙度和法向压力情况下,初始密实度大的应力应变曲线多表现为应变软化型;初始密实度小的粗粒土应力应变曲线多表现为应变硬化型.
为了定量说明软硬比随法向应力变化的规律,根据强残比与法向应力的关系特征,得到砾砂与混凝土界面在剪切过程中的应力应变特性随法向应力变化的关系,如式(1)所示:
γ=A×exp(-δ/t)+y0.
(1)
式中:γ为强残比;δ为法向应力;A,t,y0是由曲线特征确定的常数,在本式中分别取0.816,76.518,0.933,该函数的拟合效果系数R2=0.929,故可认为该计算式能够较准确地表达二者之间的关系.由式(1)可知,接触界面的强残比随法向应力的增大呈指数减小的变化趋势,当γ=1时,δ≈191.3 kPa,这意味着存在一个法向应力临界值,在此临界值两端,剪应力-剪切位移曲线发生应变软化和应变硬化两种不同的变化规律,该临界值为191.3 kPa.
2.4 界面剪胀特性
界面剪胀性受法向应力和相对密实度影响显著.首先以试样RD-A3为例,整理其剪切过程中土样法向位移,分析相对密实度一定的情况下,法向应力对界面剪胀性的影响规律.本文规定接触面土体发生剪胀时的法向位移为负,反之为正,把法向位移达到最大时的位置称为剪缩点,见图6.
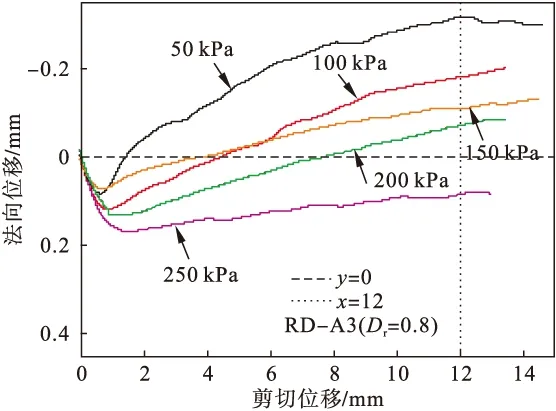
图6 试样法向位移(Dr=0.8)
由图6可知,相对密实度一定的情况下,法向位移达到剪缩点需要的剪切位移随法向应力的增大而增长.试样呈现先剪缩后剪胀,以剪胀为主的趋势.剪胀效应随法向应力的增大而减小.分析原因为法向应力较小时,剪切过程中颗粒易发生跨越、爬升等行为,故整体以剪胀为主;而法向应力较大时,剪切界面的砾砂颗粒间受法向约束较大,主要发生相互滑动或颗粒剪碎,故整体剪胀量较小.根据软化机理可知,剪胀引起的密实度减小是剪应力-剪切位移曲线软化的一个原因,故再次验证了图5中法向应力越小,应力应变曲线软化效果越显著的结论.
法向位移与剪切位移关系曲线受相对密实度影响呈现不同的变化趋势,见图7.法向应力一定的情况下,相对密实度较小时,法向位移随剪切位移的增大呈现出先增大后平稳发展的趋势,整体以剪缩为主;相对密实度较大时,法向位移随剪切位移增大呈现出先增大后减小的趋势,整体以剪胀为主,试样的剪胀性随相对密实度的增大而增大.
结合图6、图7可知,砾砂与混凝土接触面在剪切位移较小时,均产生剪缩现象,此现象可用孔隙匀化原理解释.即剪切初期,接触面为达到相对稳定的状态,需对空隙进行填补,颗粒在外力作用下互相错动,空隙变小,故产生剪缩现象.

图7 砾砂与混凝土剪切过程中试样的剪胀性
2.5 基于DIC技术的界面剪切破坏机理分析
在直剪试验中,均以人为的方式固定了剪切界面,但剪切破坏界面不仅仅发生在接触界面,距离接触面一定范围内的土体均会产生错动、翻滚等,但位移量要小于接触面的相对切向位移,从而形成一个“剪切错动带”,见图8.剪切带内土体产生应变局部化现象,产生的变形比其他部分体积内的变形大得多.
故本文采用可视化直剪盒配合双轴剪切仪,利用高像素照相设备,记录界面剪切的全过程,对砾砂和混凝土的剪切错动带的变形性状进行细观量测,对砾砂土样的位移场进行分析,进一步探讨接触界面力学性质的细观破坏机制.
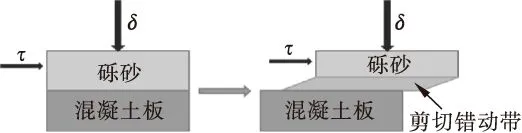
图8 剪切错动带
剪切过程中的图像大小为4 032 pixel×3 024 pixel, 1 pixel=0.033 mm.为避免边界效应对界面力学性能的影响,采集区域设为2 313 pixel×961 pixel,见图9.故将DIC分析区域外留出一定的空隙,以免由于图像边界像素点突变引起图像卷积处理失真.

图9 DIC分析区域
为了探究剪切过程中土样的位移场,将获得的砾砂与混凝土剪切全过程的数字图像,经过DIC分析处理,得到直剪过程中x方向的位移云图.图10所示为试样RD-A2(δ=250 kPa)的土样位移场云图,其中水平向右、竖直向下分别为x轴、y轴的正方向,单位为mm.
由图10可知:1)x方向的剪切位移随土样高度的增加而增大,但二者之间并非线性关系.2)剪切界面附近存在一层薄薄的剪切错动带,剪切错动带范围内的土体剪切位移较其以外的土体明显较小,水平位移分层明显,但剪切错动带以外各层土体之间位移变化相差不大,运动状态以土层的平动为主.截取图10a~10c中A-B截线上试样剪切过程中的水平位移数据,整理得到试样RD-A2的土体颗粒运动状况,见图11.由图可知,剪切错动带的厚度ht为3.2 mm,约等于3倍的D50(D50=1 mm).3)剪切错动带内的土体在剪切位移较小时,带内砾砂颗粒间位移变化相差明显,颗粒位移分布较分散,随着剪切位移的增大,带内土体剪切变化相差变小,直到最终形成1条贯通的剪切错动带,但始终与带外土体相差明显.
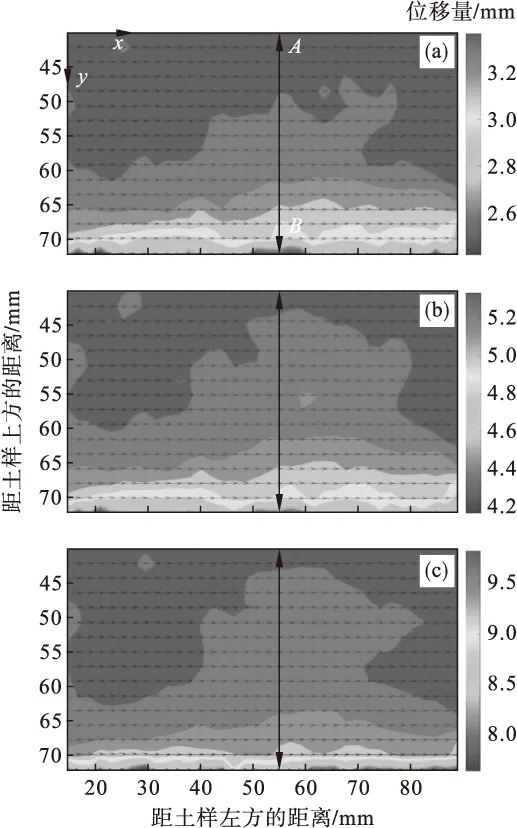
图10 不同试验阶段试样位移场分析结果(RD-A2,δ=250 kPa)

图11 不同试验阶段剪切位移曲线(RD-A2,δ=250 kPa)
3 结 论
1) 法向应力对界面应力应变曲线初始段剪切模量、峰值剪应力对应剪切位移值大小影响显著.初始段斜率随法向应力的增大而增大;法向应力较大时达到峰值剪应力所需的剪切位移较法向应力较小时变长.
2) 在常法向应力条件下,界面摩擦角随相对密实度增大呈线性增长,砾砂对混凝土的咬合作用随之变强,故相对密实度大的砾砂土样其接触面抗剪强度大多较密实度小的砾砂土样大.密实度一定的情况下,界面抗剪强度随法向应力增大呈线性增长.
3) 砾砂与混凝土接触面的应力应变曲线软化特征随法向应力的增大逐渐减弱,硬化趋势逐渐增强;得到了表征界面应力应变曲线特征随法向应力变化的计算公式,法向应力增长到191.3 kPa附近时,界面特征由应变软化转为应变硬化.
4) 界面剪切时土样发生明显的法向位移,其变化趋势与法向应力和密实度有关.相对密实度一定时,法向应力大的土样其剪胀性较小;法向应力一定时,相对密实度大的土样其剪胀性较大;剪切初期,试样法向位移随剪切位移变大而减小,不受法向应力和相对密实度的影响.
5) 由剪切过程中获得的数字图像经软件分析得到了水平方向的位移场,可以直观地看到最大的剪应变发生在接触面附近的一薄层,厚度约为3D50,最终形成了1条贯通的剪切错动带,带内土体位移较其以外明显较小.
