基于纹理图像与网格协同优化算法的三维模型压缩

董涛

摘  要：该文提出一种基于纹理图像与网格协同优化算法的三维模型压缩简化方法，在不降低三维模型视觉显示效果前提下，压缩三维模型数据。首先，对原始模型进行重网格化，获得具有规则拓扑结构的多分辨率网格;其次，结合模型网格提取纹理特征点，依据特征点确定图像有效区域;最后，利用嵌入式零树小波算法对图像进行编码和解码操作，实现对三维模型的压缩简化及图像重建。实验证明，该方法提取的图像有效区域更快捷、压缩率高、细节丰富。

关键词：纹理图像  三维模型  压缩

中图分类号：TP39    文献标识码：A 文章编号：1672-3791（2020）01（b）-0014-02

随着计算机图形图像处理技术的不断进步，三维模型技术越来越多的应用于互联网领域。浏览三维模型时，需将服务器端的模型文件传输到客户端的浏览器上，渲染生成模型，直接使用高精度模型不便于存储、传输和处理。三维技术在给用户带来真实体验的同时，也带来了庞大的模型及纹理数据量[1]。解决该问题，一方面要采取硬件方面的措施，另一方面需要图形图像方面的软件技术支持。

多年来关于三维模型的压缩与简化方面取得了较多的研究成果。Levoy首次提出直接使用点来表示和渲染三维模型表面。Michael Deering提出几何压缩方法。Beers等提出了一种纹理压缩方法。Shao Yajuan提出三维网格和纹理图像的同步压缩与渐进传输方案。Qin Aihong等提出借助一组具有值不变性的参照平面代替原有算法的预测点，提高了压缩算法精度。Sungyul Choe等设计实现了可随机读取模型局部信息的编码算法。综上所述，使用纹理图像与网格协同优化算法进行三维模型压缩尚未有人研究过。

1  该文方法概述

该文算法首先运用网格半正则化算法对原始模型进行重网格化，生成具有半正则结构的多分辨率网格，将模型的基网格作为原形，依据加入细节信息的数量建立多个层次，构建网格的四叉树结构。其次求取基网格以外的所有层次顶点实际位置和预测位置的偏移量，构建偏移量小波生成树[2]，依据特征点的分布区域及点之间的内在联系，提取感兴趣区域。最后利用嵌入式零树小波算法对图像进行编码和解码操作，实现对三维模型的压缩简化及图像重建。

2  三维模型纹理图像压缩

2.1 纹理图像与模型网格

纹理映射的过程是设备坐标到的纹理坐标的变换。给定空间曲面S∈R3，S中的随机点（x、y、z），通过纹理映射τ找到它在参数域中的对应点（u，v），可表示为：

其中，τ为纹理映射函数，模型空间点坐标（x、y、z）及其在纹理空间的对应坐标（u，v）均是已知信息，我们可以先提取三维模型网格的特征顶点，并将其映射到纹理贴图坐标系中，获取感兴趣区域的特征点。这些特征点必然分布在纹理图像的可见区域，并且集中在模型细节丰富区域，最后依据图像纹理的连续性，可获取纹理图像的关键区域。

2.2 模型网格和纹理图像的特征点提取

为方便提取模型网格的几何信息，可以将模型的基网格作为原形，依据加入细节信息的数量建立多个层次，构建网格的四叉树结构。该文采用基于多分支的半正则化方法对原始模型网格进行重构，构建半正则化拓扑结构网格。半正则网格的面具备树形细分结构，边和边上的点也同样是树形结构。

该文按照c1→c2→…→cn的顺序对适合我们需求层次的偏移量小波系数集合ci（i=1，2，…，n）进行如下操作：首先对当前集合，设阈值。将ci中各个小波系数cij（1≤j≤i）依次与阈值ωi比较，若小波系数大于阈值，则选择该小波系数所属的三维点作为备选特征点。其次检测当前分辨率下的集合中所有符合条件的特征点数目，如果数目大于预设值，则将当前阈值增大一倍，继续求取备选特征点，直到特征点数目小于等于预设值，将所有备选点保存为特征点。对每个特征点vp，从原始模型网格中提取与特征点空间距离最小的点vm，并根据原始网格中每个顶点在纹理空间的映射位置，获取该点在纹理图像上的对应像素点，即为纹理图像特征点Pvm。

2.3 纹理图像感兴趣区域的提取与变换

模型网格特征点提取后，依据特征点的分布区域及点之间的内在联系，便可以提取纹理图像感兴趣区域。对于某一感兴趣区域而言，临近特征点的纹理坐标比较接近，因此可以把纹理图像特征点的坐标作为研究对象，依据坐标的相似程度对各个特征点进行深入分析，分成若干个类。将物理或抽象对象的集合分成由类似对象组成的多个类的过程被称为聚类[3]。通过对纹理图像特征点进行聚类，可以实现图像感兴趣区域的提取，可以对图像小波变换域的系数进行进一步处理。

依据获得的特征点分布情况，我们可以在纹理图像上进行计算，划分若干个包含特征点的矩形选区，对选区包含的数据点进行四叉树分割，每个末端节点内包含若干特征点，然后定义四叉树叶子节点中心的一个特征点为种子点，将获得n个种子点标记为待聚类的中心。聚类时的点集不受叶节点内点的限制，重复计算每个点到聚类中心的距离，将点归类到距离最近的类中去，直到算法的结果收敛，不能被聚类的点认为是噪声点。提取包含一个类所有特征点的矩形选区，这些矩形选区就是我们要提取的纹理图像感兴趣区域。

对原图像进行分解，将相邻像素差值折半后存储到高频带，相邻像素的均值存储到低频带，这样就对纹理图像完成了一次小波分解。如果需要对图像实施进一步小波变换[4]，仅需针对原圖像的低频区域操作即可。经过小波变换后，可以获得一幅包含多层次分辨率的图像。对原始图像变换后提取的感兴趣区域进行编解码时，需适当调整区域内部的小波系数。该文采用最大位移法[5]，位移因子f满足f≥max（Ma），Ma是小波系数幅值位平面的最大值。经位平面提升的区域内小波系数的最小幅度大于背景小波系数的最大幅值。以幅值2f为阈值，幅值大于阈值为感兴趣区域小波系数，反之为背景小波系数。通过该方法可以确定感兴趣区域小波系数，如果将这些系数右移f位，即可还原感兴趣区域系数。

2.4 纹理图像编码与重建

该文采用嵌入式零树小波算法对图像进行编码，结合小波图像多层的数据形态，改善小波系数的组织方法，减少不重要系数的位运算次数，确保重要的小波系数被优先表示和编码，并尽可能提高相关的峰值信噪比，以期提高图像重建质量。根据数据先选择一个初始阈值T0，T0>，其中Gmax是最大的小波系数，接下来每次扫描的阈值是前次扫描阈值的一半。然后进行主辅扫描，扫描中访问到的每个系数都分类到正显著（POS）、负显著（NEG）、零树根（ZTR）、孤立零（IZ）4个符号中，最终输出编码信号。

运用嵌入式零树小波算法对变换后获取的小波系数进行编码，对于编码后的输出结果，可以采用Huffman Coding方法二次压缩，最终生成纹理图像的二进制代码文件。在三维模型的传输过程中，解码器采用相反的操作过程，利用接收到的小波系数重建模型纹理图像。在解码恢复图像的过程中，首先恢复最重要的系数，再恢复阈值减半后控制输出的系数。

3  实验与结果分析

对实验三维模型进行压缩，采用最大位移法对模型纹理图像小波系数进行处理后，再对小波系数进行嵌入式压缩编码和熵编码，模型原始大小为8.21MB，采用上述方法对模型进行压缩简化处理后，获得的二进制压缩文件大小为0.26MB，压缩后文件与原始纹理贴图的压缩比为3.2%。解码重建时，解码器对纹理图像感兴趣区域系数优先解码，获得重建图像。各频带经过位移提升的系数优先传递给解码器，感兴趣区域解码后，快速获得了清晰度较高的重建图像。

解压前，试验模型感兴趣区域小波系数的二进制码的数据量为0.12MB。用不完全解码的文件重建纹理图像，对模型进行贴图映射，获得三维模型重建图像。模型纹理图像分辨率低的部分对模型表面集合细节复杂部分的影响较小。感兴趣区域分辨率较高，贴图纹理清晰、精细。而细节较少的次要区域图像的纹理分辨率较低。使用压缩文件中的部分数据可以快速取得理想的三维模型纹理图像重建效果。

最后，对压缩文件的其余部分进行解码。对原始纹理贴图进行小波变换时，小波系数的损失精度限于小数点后数位，对系数幅值产生的影响可忽略，利用这些系数可精确还原模型纹理图像。解码后生成的纹理图像与感兴趣区域重建图像。重建后，三维模型的纹理图案保持了很高的分辨率，解码器能准确的重建原模型的颜色信息。

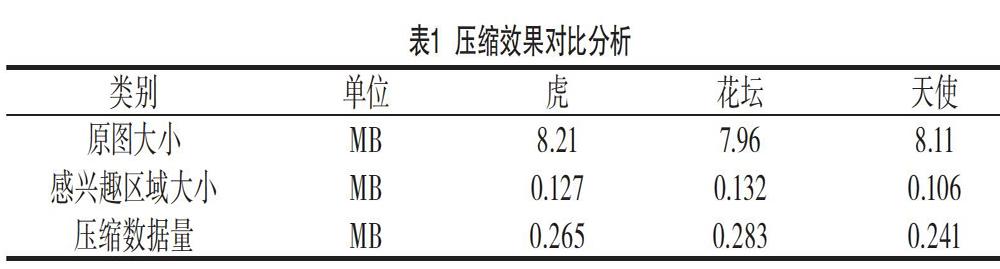
表1中记录了实验模型压缩前的文件大小;经过嵌入式零树小波算法压缩后的文件的大小;优先传输的文件大小。

4  结语

该文针对三维模型纹理图像的压缩简化过程进行了深入研究，提出了基于纹理图像与网格协同优化的三维模型压缩算法，构建针对三维模型纹理图像的编解码实验平台，对压缩简化算法进行验证，取得了较好的实验效果。该文算法需浏览原始模型网格全部顶点，依次提取原网格顶点中与每一个半正则网格特征点距离最近的顶点，进一步提取纹理图像特征点，巨大的特征点数量必然会降低算法的计算效率。后续研究会尝试建立更合理的数学模型，进一步提高算法的执行效率。

参考文献

[1] 武艳芳.基于Web3D的产品虚拟展示与用户定制[J].图学学报，2012（13）：85-89.

[2] 马建平，罗笑男，陈渤，等.面向移动终端的三角网格逆细分压缩算法[J].软件学报，2009（19）：2607-2615.

[3] 刘铭，刘秉权，刘涵超，等.面向信息检索的快速聚類算法[J].计算机研究与发展，2013（7）：1452-1463.

[4] 康学净.面向移动物联网应用的小波图像去噪及压缩方法研究[D].天津理工大学，2012.

[5] 晏秀梅.基于小波和轮廓波变换的感兴趣区域编码研究[D].中南民族大学，2010.