基于Revit二次开发的多面体参数化建模
2020-04-07
(大连理工大学 建设工程学部,大连 116024)
引言
类Weaire-Phelan多面体(简称类WP多面体)是由Weaire-Phelan多面体气泡单元衍生、改良而成的一类多面体[1]。其数学理论起源是Kelvin问题:将无限空间划分为具有一定界面面积的等体积单元(或其组合),什么样的划分方式能够使得界面面积取最小值。Weaire-Phelan气泡对应的空间分割方案是目前已知的Kelvin问题的最优解[2]。该数学理论在结构设计上最经典的应用就是国家游泳中心“水立方”的多面体空间刚架结构。

图1 国家游泳中心“水立方”
BIM技术不仅用于解决项目中智能分工与协同、异形体设计、建筑分析、可视化、精细化等二维设计难以解决的困难,而且使项目管理逐步形成新的管理体系[3-5]。Revit作为BIM技术的重要平台,近年来在二次曲面网壳结构、斜拉桥和单层工业厂房的参数化设计,识别构件点云数据,自动化计算窗户热物理特性,PKPM接口等方向均有研究进展[6-11]。但从现有资料来看,基于Revit开发的建模方法并没有涉及类WP多面体空间结构这一经典类型。该空间结构独特的“嵌填”式[12]的建模思路极大的区别于当下大多数模型软件“搭积木”式的建模方法。
文献[1]研究了组成类WP多面体的两种基本单元,完成了基本12面体和基本14面体的图形解析和数学解析,确定了基本多面体的形状控制参数,分析了形状控制参数与多面体边长的数学相关特性,规范了形状控制参数的合理取值范围,为多面体的参数化三维建模程序奠定了基础。文献[12]提出了类WP多面体基于AutoCAD的建模方法,并提供了多面体基本组合的建模思路。本文在分析这些研究成果的基础上,利用Revit提供的API函数,完成类WP多面体基本单元和基本组合的建模程序插件,实现基本单元和基本组合的参数化选型和可视化建模功能,以提高类WP多面体结构选型时的工作效率。
1 基于Revit的多面体建模开发
本文基于Revit 2018及Revit 2018.2 SDK,选择Visual Studio Community 2017为平台,编译程序目标框架选用.NET Framework 4.6,在Windows7(x64)版本系统下,使用C#(6.0版本)编程语言完成程序编写和编译。主要工作包含两部分内容:多面体基本单元的建模和多面体基本组合的建模。
1.1 总体架构
在数学理论、建模方法和编程技术的支撑下,首先设计和编制基本单元和基本组合的数据处理模块,根据输入参数计算生成点、线、面等数据,然后交由建模模块在Revit视图界面中生成可视化模型。总体架构如图2所示。
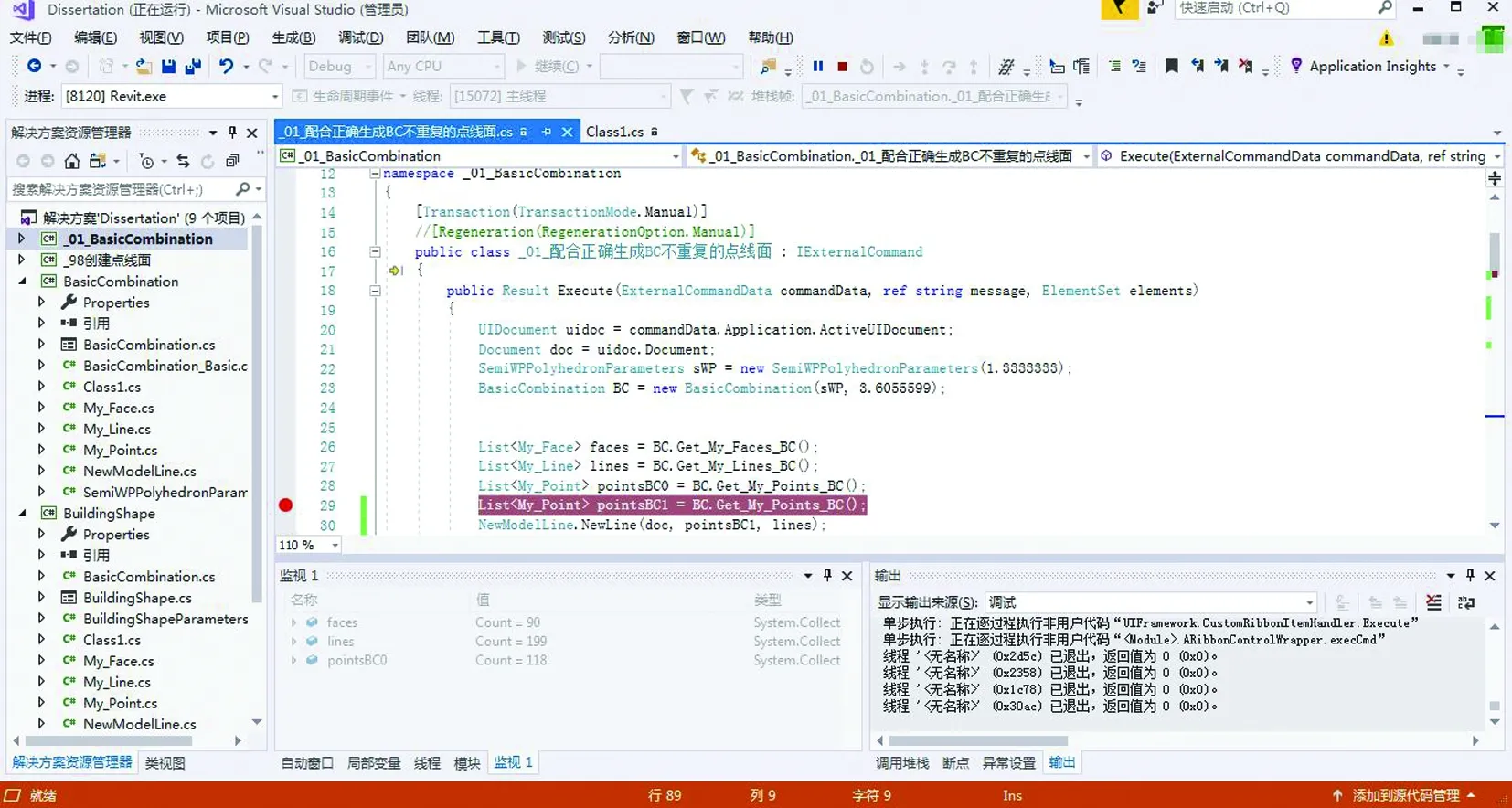
图3 开发调试界面

图2 总体架构
1.2 程序开发
程序开发工作主要包括以下几个方面[13]。
①在Visual C#中新建一个类库,通过添加RevitAPI接口并引用Autodesk.Revit的命名空间,指定事物模式和模型更新模式,从ExternalCommand接口实现新建类。
②对Execute方法重载,在Visual C#中新建窗体创建可视化界面并进行参数的传入;
③参数修改,若程序执行结果不满足设计要求,则需要重新修改参数
④生成多面体模型。
利用API为Revit编写建模插件的开发调试界面如图3所示。
2 多面体基本单元建模
2.1 类WP多面体的形状控制参数
2.1.1 类WP多面体基本单元
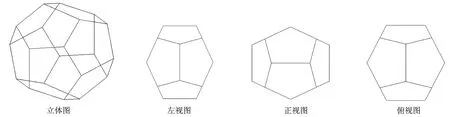
类WP多面体由两种基本多面体组合而成,一种是12面体(所有面均为5边形),一种是14面体(12个面为5边形, 2个面为6边形)。
基本12面体由12个全等的5边形组成。这些5边形并不是正5边形,而是等腰5边形,也即它有两种边长,其中4条边长度相等。
基本14面体由12个5边形和2个相互平行的6边形组成。这些5边形中,有4个与基本12面体的5边形一致,其余8个则相互一致属于另外一种5边形,也即基本14面体包含3种平面多边形。
2.1.2 提取形状控制参数
在边长为4的晶格立方体中,取基本12面体的体心为坐标原点,基本12面体单元的20个顶点坐标如下:
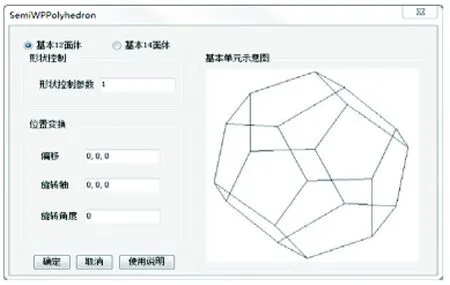
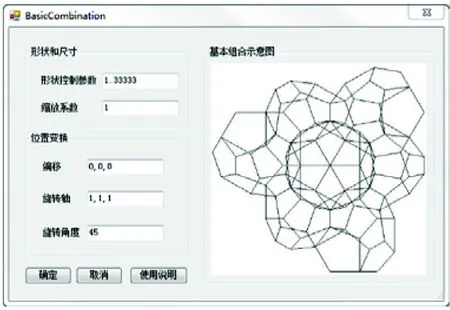
(±a,±a,±a),其中0 (0,±b,±c),(±b,±c, 0)(±c, 0,±b),其中0 类似的,取边长为4的晶格立方体,取基本14面体的体心为坐标原点。基本14面体单元的24个顶点坐标如下:(1-a,±(2-a),±a),(1-c,±(2-b), 0)(1,±(2-c),±b),(-1+a,±a,±(2-a)),(-1+c, 0,±(2-b)),(-1,±b±(2-c)),(1, 0,±1),(-1,±1, 0)。 从理论上讲a、b、c均可以作为独立参数控制类WP多面体的顶点坐标,考虑到c恰好是基本多面体其中一条棱边的边长,因此这里将c确定为类WP多面体的形状控制参数。其中,形状控制参数c的合理取值范围是(1.0~1.5)[1]。 下面以基本12面体为载体阐述参数化建模的实现过程。实现基本14面体的参数化建模方法与之类似。在程序代码中,为了方面记忆和识别,形状参数被定义为double类型的字段,字段名称为shape; a、b也是double类型,其中a=(2.0/3.0)×shape,b=0.5×shape。 2.2.1 确定点、线对应关系 文献[1]虽然给出了两种基本多面体的顶点坐标,但是并未明确顶点与棱边的对应连接关系。因此,首先需要解决的问题就是基本多面体单元的点、线对应关系。 两种多面体有一定的特殊性:若将多面体的所有顶点两两连线,并将这些线段按照长度升序排列。那么所有正确的棱边一定连续的排列在该升序序列的头部。也即正确的棱边总是这些线段中的较短部分。 第一步,将12面体的20个顶点依次输入,编号并储存。 XYZ p1=new XYZ(0,b,shape); XYZ p2=new XYZ(0,-b,shape); ……XYZ p12=new XYZ(-shape, 0,-b); XYZ p13=new XYZ(a,a,a); ……XYZ p20=new XYZ(-a,-a,-a); List 第二步,将这20个顶点两两配对成不重复的组合,计算每对组合两顶点之间的距离并储存至distancesList,同步储存此时对应的顶点编号至pointPairs。 //储存两点之间的距离List 第三步,将储存距离的集合复制一份并按照升序排列。取该序列的第1个值为限值min1,取该序列的第30个值为限值min2。这是因为基本12面体有30条棱边。将间距满足限值的顶点组合输出到TXT文件。相应的,在处理14面体的类似问题时要取该序列的第一个值为限值min1,取该序列的第36个值为限值min2,这是因为基本14面体有36条棱边。 double[]distancesArray=distancesList.ToArray(); Array.Sort(distancesArray); //数组升序排列double min1,min2; min1=distancesArray[0]; //拿到第一个限值min2=distancesArray[29]; //拿到第二个限值//判断距离,将对的坐标对和距离绑定并输出for(int i=0; i 图4 点、线对应关系 最后,查看TXT文件,结果文件如图4所示。以文件“Create12结果-30根线.txt”的数据为例:每一行有3个数据(点编号,点编号,两点之间的距离),代表基本12面体的一根棱边的两个端点,以及该棱边的长度。该文件能够解决两个问题:第一,程序在输出某个线模型时,可知这条线是由哪两个点连接而成的; 第二,程序中代表线的数据类型只需要存储点编号即可。类WP多面体两种基本单元的顶点与棱边对应连接的关系即可据此确定。 图5 基本12面体 2.2.2 多面体基本单元建模 将上述点、线对应关系储存起来。储存点用List 如图5和图6分别是组成类WP多面体的基本12面体和基本14面体的模型线建模效果图。图中类WP多面体的形状控制参数shape=1.333333,是“水立方”Water-Cube多面体的形状参数值。 3.1.1 基本组合的构成 文献[12]对类WP多面体基本组合的构成进行了深入的研究。为了方便说明,下文仍取边长为4的晶格立方体来阐述基本组合中每个基本单元的变换方式和它们的相对位置。如图7展示的是2+6基本多面体组合中各个基本单元体心的相对位置。其中“圆环”代表12面体体心位置,“圆球”代表14面体体心位置。 下文用到的12面体和14面体满足:顶点的相对位置与基本多面体一致,体心定位在相对坐标系的原点。另外,旋转操作中的旋转角度和旋转轴满足右手规则。下面依次介绍2+6基本组合中的每个基本单元该如何变换和定位: 图6 基本14面体 图7 多面体基本组合中多面体体心分布示意图 ①12面体定位在坐标原点; ②14面体定位在(1, 0,-2); ③复制 ① 中的12面体,将复制体绕Z轴旋转90°,再将其定位到(-2, 2,-2); ④选择YZ平面为镜像平面,将 ② 确定的14面体镜像生成一个新的14面体,新多面体体心位置在(-1, 0,-2); ⑤取一个14面体,体心在(0, 0, 0)绕Z轴旋转90°,再将其定位到(-2,-1, 0); ⑥选择ZX平面为镜像平面,将 ⑤ 确定的14面体镜像生成一个新的14面体,新多面体体心位置在(-2, 1, 0); ⑦取一个14面体,体心在(0, 0, 0)绕Y轴旋转90°,再将其定位到(0, 2, 1); ⑧选择XY平面为镜像平面,将 ⑦ 确定的14面体镜像生成一个新的14面体,新多面体体心位置在(0, 2,-1); 通过上述8次操作即可得到一个类WP多面体空间结构的2+6基本组合。 3.1.2 确定基本单元的实际尺寸 基本单元尺寸的定义[15]:将属于基本单元的一个14面体中的2个相互平行6边形平面之间的距离定义为类WP多面体的基本单元尺寸。具体到边长为4的晶格立方体对应的基本单元的尺寸为1.5shape。再考虑其放大或缩小问题,定义比例系数scale,则实际工程应用中结构的基本单元尺寸为1.5 shape×scale。 3.2.1 缩放两种基本单元 2+6个多面体在基本组合中的位置是具有相对性的。因此,缩放基本单元的尺寸即可对应形成等比例缩放的基本组合。也即先缩放基本单元的顶点坐标; 然后在变换基本单元拼装成基本组合时,将单元体心的相对坐标也按照比例系数等比例变换。 3.2.2 拼装基本组合 按照4.1节的介绍,依次完成基本组合拼装。首先,复制一份基本多面体单元的点、线、面集合供本次操作调用; 其次,如果有必要变换的话,对集合副本进行变换操作(平移,旋转,镜像等); 最后,将完成变换的副本数据对应添加进基本组合的点、线、面集合。 在拼装过程中,除了点集合的操作,还会涉及对线集合和面集合储存对象编号的累加问题,多面体体心定位问题,多面体旋转、镜像、深拷贝问题等。这些问题都可以抽象成自定义函数。 3.2.3 基本组合建模 如图8是类WP多面体基本组合的模型线建模效果图。图中类WP多面体的形状控制参数shape=1.333333,比例系数scale=3.6055599,均为“水立方”Water-Cube多面体的控制参数值。 多面体空间结构的几何构成十分复杂,按照建筑和结构的要求对其进行优化和选型是一项非常重要的工作[16]。主要是为了满足建筑效果和结构构造这两方面的要求。 首先,形状控制参数的合理取值范围是1.0~1.5; 其次,选型过程中不考虑缩放系数的影响; 最后,考虑到形成多面体空间结构之前,基本单元往往要旋转、切割,所以要让多面体顶点在X、Y、Z三个平面上的投影尽可能多的重合。 4.2.1 基本12面体选型对比 选择4个形状控制参数做对比。分别是1, 1.2599, 1.33333和1.4。参数输入界面如图9,可以通过偏移坐标控制不同参数的基本12面体的生成位置,让其处于同一视图中方便观察对比。 建模结果如图10所示。图形的形状控制参数从左往右依次对应等于1, 1.2599, 1.33333和1.4。形状控制参数只影响12面体的大小,作用类似于缩放系数。 图9 参数输入界面 图10 12面体建模结果的三维视图 4.2.2 基本14面体选型对比 同样选择4个形状控制参数做对比。分别是1, 1.2599, 1.33333和1.4。观察建模结果的俯视图,如图11,图形的形状控制参数从左往右依次对应等于1, 1.2599, 1.33333和1.4。当形状控制参数等于1.33333时较为符合选型原则。 图11 14面体建模结果俯视图 4.2.3 基本组合建模 输入控制参数。形状控制参数为1.33333,缩放系数为1,绕(1, 1, 1)旋转45°,不做位置变换。输入界面见图12。建模结果如图13所示。 图12 参数输入界面 图13 基本组合建模结果 本文基于Revit进行二次开发,结合类WP多面体的数学理论和建模方法,利用参数化实现了多面体基本单元的选型、建模和基本组合的建模。运行结果表明,该方法能够正确创建基于不同参数的类WP多面体,为设计者提供了一种方便的可视化设计新方法,本研究成果可直接用于BIM产生多面体空间结构。2.2 参数化建模




3 多面体基本组合建模
3.1 类WP多面体基本组合的构成及尺寸


3.2 参数化建模
4 类WP多面体选型应用
4.1 选型原则
4.2 参数化选型与建模



5 总结
