多普勒测速雷达辅助捷联惯导系统空中精对准方法

杨 波，杨小冈，席建祥，刘云峰

（1. 火箭军工程大学导弹工程学院，西安 710025；2. 火箭军装备部驻成都地区第四军事代表室，成都 610052）

飞行器在特殊紧急情况下应能实现应急机动。捷联惯导系统作为飞行器上重要导航设备，其进入导航工作之前必须先进行初始对准，倘若能够在飞行器飞行过程中快速实现高精度空中对准，将对飞行器的快速反应、应急机动具有重要的意义[1]。目前，捷联惯导系统空中对准主要采用传递对准或卫星辅助对准。对于空中传递对准，前提是飞行器上配备有高精度主惯导系统，以此作为参考基准，但很多飞行器并不具备这一条件，而且传递对准对杆臂效应补偿、挠曲变形建模的要求较高[2,3]。文献[4-5]利用卫星导航接收机的输出信息，与惯导系统输出构成量测，通过滤波实现空中对准，考虑到实际使用时卫星信号受外界环境和人为因素影响较大，导致这种对准方式的可靠性和抗干扰性一般，而且INS/卫导组合的对准时间较长，限制了其在战场环境以及特殊情况下的应用。文献[7]研究了利用里程计辅助车载捷联惯导系统实现运动基座对准，具有自主性强、抗干扰性好的优点，但只能用于陆地车载条件。

多普勒测速雷达基于多普勒效应，利用雷达发射的电磁波与回波之间的频率差异来获得载体运动的速度信息，具有精度高、无积累误差、输出连续、自主性强、抗干扰性好等突出优点[6,7]。在航海领域，通常利用多普勒测速仪（Doppler Velocity Log，DVL）辅助水下航行器、舰船中的惯导系统完成行进间对准，并取得良好的应用效果[8-10]，但目前多普勒测速雷达用于飞行器中惯导系统空中对准方面的研究不多。为此，本文提出在飞行器飞行过程中采用多普勒雷达的测速信息辅助捷联惯导系统实现空中精对准，在对多普勒测速雷达进行误差分析建模的基础上，根据捷联惯导的姿态矩阵与多普勒雷达的速度输出构造导航坐标系下等效速度输出，利用该等效速度输出作为辅助对准的量测信息，采用卡尔曼滤波完成空中精对准。

1 空中精对准方案

在飞行器飞行运动过程中，捷联惯导系统已通电，可利用飞行器上配备的三轴磁强计或双天线卫星等设备粗略确定飞行器的初始航向姿态信息，并装订到捷联惯导系统中，完成捷联惯导系统的空中粗对准。粗对准的精度不高，一般在数度左右，这主要取决于上述航向姿态确定设备的自身精度。

粗对准结束后即可进行精对准。在精对准过程中，捷联惯导系统经粗对准后即进行正常导航解算与参数输出；然后，借助捷联惯导系统的姿态输出，将多普勒测速雷达输出的载体坐标系下速度转换到导航坐标系下，获得多普勒雷达的等效速度输出；接着，以捷联惯导与多普勒雷达的误差作为精对准的系统状态，精对准的量测选为捷联惯导速度输出与多普勒雷达等效速度输出之间的差值；在此基础上，利用精对准卡尔曼滤波计算得到惯导失准角等系统状态的最优估计结果。此时，该估计结果可以用来校正捷联惯导姿态矩阵的误差，即最终实现惯导空中精对准。上述空中精对准的原理方案如图1 所示。

2 多普勒测速雷达的误差模型

为了有效避免杆臂效应的影响，可以将捷联惯导系统和多普勒测速雷达的中心尽可能安装在同一垂线上，此时刻度系数误差和安装误差则是多普勒测速雷达主要的误差源。其中，刻度系数误差是最重要的误差源，其通常可考虑为随机常值，即

由于多普勒雷达与捷联惯导系统的安装轴线难以一致，因此必然存在一定的安装误差。考虑到实际应用中通常是将两个设备固联安装在飞行器上，待安装固定后它们的安装角通常不易发生明显变化，因此可以将多普勒雷达与捷联惯导之间的安装误差也考虑为随机常值，其满足

3 多普勒测速雷达辅助精对准滤波算法

在辅助精对准的过程中，将采用卡尔曼滤波间接法对捷联惯导系统的失准角进行估计，为此需要以捷联惯导系统与多普勒测速雷达的误差作为系统状态，建立相应的状态方程；同时，利用两种导航设备的输出构造精对准的量测，建立量测与状态之间的关系，从而获得精对准的量测方程。

3.1 辅助精对准的状态方程

根据捷联惯导系统、多普勒测速雷达的误差模型，选取精对准的状态，其具体包括平台失准角φ E,φ N,φU，速度误差δ v E,δ vN,δvU，位置误差δ L,δλ,δh，陀螺常值漂移ε bx,ε by,εbz，加速度计常值误差 ∇bx, ∇by,∇bz；多普勒测速雷达的刻度系数误差δK x,δK y,δKz，安装误差角δ Ax,δAy,δAz。即辅助对准的系统状态X为：

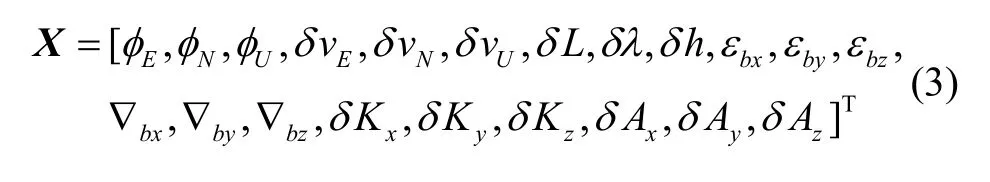
显然，基于两种导航设备的误差模型，不难将空中精对准的状态方程描述为

这里，F 、G、W分别为系统的状态矩阵、噪声驱动阵、白噪声序列，W=[wg x,wg y,wg z,wa x,wa y,waz]T，其中wg x,wg y,wgz为陀螺白噪声，wa x,wa y,waz为加速度计白噪声。

3.2 辅助精对准的量测方程

设载体坐标系为右前上坐标系，即坐标系的三个轴分别沿着载体的横轴向右、纵轴向前以及航向轴向上；导航坐标系为东北天地理坐标系，即坐标系的三个轴分别指向地理东向、地理北向以及沿着垂线指向天向。

多普勒测速雷达通常沿着载体坐标系的三个轴进行安装。由于多普勒测速雷达输出的速度是载体运动速度在载体坐标系下的投影形式，而捷联惯导系统输出的速度则是载体运动速度在导航坐标系下的投影形式，为了利用上述两个系统输出的速度构造辅助对准的量测，需要利用捷联惯导系统输出的载体姿态矩阵，将多普勒测速雷达的速度输出由载体坐标系转换到导航坐标系下。

设多普勒测速雷达输出的载体运动速度在载体坐标系下投影形式为；捷联惯导系统输出的载体运动速度在导航坐标系下投影形式为，载体姿态矩阵为则可构造出多普勒测速雷达辅助捷联惯导对准的量测为

记导航坐标系下载体的真实速度为nV，真实姿态矩阵为捷联惯导的速度误差为δVn，数学平台失准 角 为Φ，这里δVn=[δ v E,δ vN,δvU]T，Φ=[φ E,φ N,φU]T，则式(5)可变为

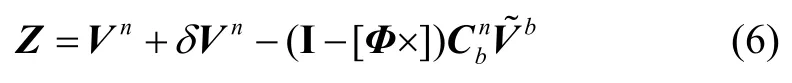
式中，[Φ×] 为矢量Φ的反对称矩阵，即

设多普勒雷达的安装误差矩阵为[δ A] ，刻度系数误差矩阵为[δ K] ，则式(6)可进一步表示为

于是，将式(7)右边展开，并经整理可得

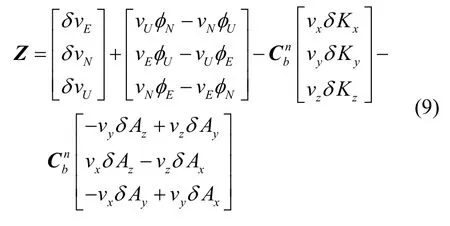
再将式(9)进一步写为如下形式

从而根据式(3)与(10)，不难将空中精对准的量测方程表述为

这里，量测矩阵H=[H1O3×9H2]。

于是，基于上述状态方程(4)和量测方程(11)，利用tk时刻的量测Zk可实现空中精对准滤波解算，进而获得惯导系统失准角等状态的最优估计结果。此时，需要根据该估计结果来校正捷联惯导系统的数学平台姿态误差，即实现空中精对准，具体修正方法如下。

设捷联惯导系统实际建立得到的导航坐标系分别为n′系，实际解算得到的姿态矩阵为其中n′系相对n系存在误差角Φ=[φ E,φ N,φU]T。于是，利用前面滤波计算所得到的数学平台失准角估计值可以计算出n′系到n系的转换矩阵即

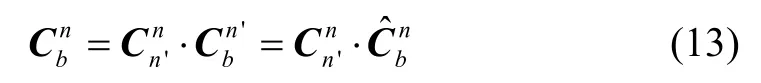
从而，利用上述方法就实现了对捷联惯导系统数学平台失准角的在线修正。

4 仿真与分析

不妨设多普勒测速雷达的刻度系数误差为0.5%，沿载体坐标系三个轴的安装误差分别为20 ′、12 ′、15 ′，测速噪声为0.05 m/s；捷联惯导中陀螺仪、加速度计的常值误差分别为0.02 °/h、5×10-5g，其白噪声随机游走分别为粗对准完成后，水平姿态误差为1 °，方位误差为3 °；辅助精对准的仿真时间取为900 s，对准过程中载体始终处于飞行运动状态。

设计三种不同的载体飞行运动轨迹，对文中所研究的空中精对准方法分别进行100 次仿真验证，每次仿真结果先取绝对值，然后对100 次仿真结果的绝对值求均值，并利用该均值衡量精对准精度。

在飞行轨迹1 中，先后设置了加速、爬升、匀速、转弯等机动形式，飞行轨迹曲线如图2 所示，精对准仿真验证结果如图3-5 所示。

图2 载体飞行轨迹1 三维曲线Fig.2 Three dimensional curve of trajectory 1

图3 东向失准角的估计误差（基于轨迹1）Fig.3 Estimation error of east misalignment angle（based on trajectory 1）

图4 北向失准角的估计误差（基于轨迹1）Fig.4 Estimation error of north misalignment angle（based on trajectory 1）

图5 天向失准角的估计误差（基于轨迹1）Fig.5 Estimation error of azimuth misalignment angle（based on trajectory 1）

根据图3-5 不难发现，通过空中对准使捷联惯导系统数学平台的三个误差角取得了有效收敛：其估计误差分别控制在0.3 ′、0.1 ′和0.5 ′。相对而言，天向失准角的估计时间明显长于两个水平失准角（前者约为420 s，后者约为180 s），而且天向失准角的误差收敛与第400 s 时载体开始作转弯机动有关。仿真结果表明，多普勒测速雷达测得的载体速度信息为捷联惯导空中精基座对准发挥了关键作用，而且效果显著。同时也可以看出，相比之下，天向失准角的估计精度略低，特别是估计误差达到稳态的时间相对较长，这是由于在空中精对准的状态空间模型中，天向失准角的可观测性较差，从而导致天向失准角的估计效果不够理想。而仿真中载体作转弯机动有效改善了天向失准角的估计效果，也直接证明了这一点。

在飞行轨迹2 中，为了从反面考察载体机动对捷联惯导空中精对准的影响，直接令载体始终作匀速直线运动，飞行轨迹三维曲线如图6 所示。基于飞行轨迹2，其他仿真条件均保持不变，仿真验证结果如图7-9所示。

图6 载体飞行轨迹2 三维曲线Fig.6 Three dimensional curve of trajectory 2

图7 东向失准角的估计误差（基于轨迹2）Fig.7 Estimation error of east misalignment angle（based on trajectory 2）

根据仿真结果图7-9 可以看出，捷联惯导系统水平对准的精度几乎不受载体机动的影响，而方位对准的精度和效果则明显受到影响：在无任何机动条件下，东向、北向失准角的估计精度分别达到0.3 ′和0.2 ′，而且不到90 s 就达到稳态；而天向失准角的估计误差到第500 s 以后才开始收敛，最终估计精度约为1.4 ′。

图8 北向失准角的估计误差（基于轨迹2）Fig.8 Estimation error of north misalignment angle（based on trajectory 2）

图9 天向失准角的估计误差（基于轨迹2）Fig.9 Estimation error of azimuth misalignment angle（based on trajectory 2）

通过基于前两种轨迹的仿真验证可以看出，为了有效提高天向失准角的估计精度，可以考虑在载体运动中加入航向辅助机动，从而提高捷联惯导系统天向失准角的可观测性。

为此，在飞行轨迹3 的设计中，载体首先作100 s匀速直线飞行，然后进行60 s 的右转弯和左转弯航向机动，之后一直作匀速直线飞行，飞行轨迹如图10 所示。基于飞行轨迹3，其他仿真条件保持不变，对文中所研究的精对准方法进行仿真验证，重点考察天向失准角的估计效果，如图11 所示。

图10 载体飞行轨迹3 三维曲线Fig.10 Three dimensional curve of trajectory 3

图11 天向失准角的估计误差（基于轨迹3）Fig.11 Estimation error of azimuth misalignment angle（based on trajectory 3）

仿真结果图11 表明，在航向机动的辅助下，多普勒测速雷达辅助捷联惯导系统空中精对准的效果得到明显改善：方位对准精度大幅提高，稳态值优于0.3 ′；与此同时，方位对准时间明显缩短，其估计误差从第100 s 就开始明显快速收敛，远远短于前面两种轨迹下的方位对准时间。这是因为载体从第100 s 开始作右转弯和左转弯航向机动，有效提高了天向失准角的估计效果。由此可见，航向辅助机动对于提高精对准精度、缩短精对准时间发挥了重要的作用，而且在空中对准过程中飞行器实现航向机动也比较容易。

5 结 论

为了实现在卫星拒止条件下捷联惯导系统在飞行器飞行过程中实现精对准，本文提出一种利用多普勒测速雷达辅助其进行空中精对准的方法。基于捷联惯导输出的姿态矩阵与多普勒雷达的速度输出，计算得到导航坐标系下雷达等效速度输出，将其与捷联惯导实际速度输出之间的差值选为精对准的量测；采用卡尔曼滤波完成空中精对准。该方法精度高、自主性强，不易受外界干扰，而且工程易于实现，特别适用于特殊紧急情况时飞行器的快速反应与应急机动。