基于刚度退化模型的连续刚构桥梁损伤指数计算
2020-04-03李民伟
李民伟
云南省交通运输厅工程质量监督局
1 引言
连续刚构桥同时具备T 型刚构桥与连续梁桥的优点,其结构受力较为合理、行车条件良好、外形简洁美观、施工工艺成熟,同时具备较大的跨越能力,在山区桥梁建设中应用广泛,其抗震能力设计是该桥型设计时的重要工作内容。采用损伤指数及其数学模型评估桥梁的抗震性能具有简明扼要的特点,在连续刚构桥抗震设计中具有一定的工程实用价值。
2 损伤指数的计算方法
2.1 刚度退化模型
目前,桥梁结构遭受地震作用后的损伤评估多采用基于最大反应与累积耗能的Park-Ang 模型[1]~[4],但该模型参数多、权重值不易确定,不利于工程应用。本文采用Ghobarah 提出的刚度退化模型[5]进行桥梁地震作用下损伤指数的计算,该模型具有概念明确、参数相对较少等特点,其计算方法如下:

式中:
DM——桥梁地震作用下的损伤指数;
Kf——桥梁遭受地震后的整体刚度;
Ki——桥梁遭受地震前的整体刚度。
2.2 刚度计算方法
在Ghobarah 提出的刚度退化模型中,桥梁地震作用下损伤指数计算的关键是确定其在地震前、地震后的整体刚度。本文采用Ghobarah提出的二次推倒分析方法来计算桥梁在地震作用前后整体刚度的变化,首先是在桥梁遭受地震作用前对其进行推倒分析,确定其在地震前的整体刚度Ki;其次是当桥梁遭受既定地震作用后,回到静止无荷载状态的条件下对其进行推倒分析,确定其在遭受地震作用后的整体刚度Kf。
2.3 损伤指数的计算步骤
(1)根据桥梁设计文件,建立有限元计算模型,采用基于桥梁特征值分析的振型荷载作为推倒分析时的侧向荷载。
(2)进行桥梁地震作用前的推倒分析,获得其在顺桥向、横桥向的初始整体刚度、屈服位置、屈服位置对应的屈服位移。
(3)根据桥梁地震作用前的推倒分析结果及其在地震作用下的时程分析结果,对屈服位置的刚度按下式进行修正:

式中:
Keff——修正后的有效刚度;
K0——原始刚度;
μ——位移延性比。
(4)进行桥梁地震作用后的推倒分析,获得桥梁在遭受地震作用后顺桥向、横桥向的整体刚度。
(5)根据桥梁地震作用前后的刚度变化,按(1)式计算其在既定地震作用下的损伤指数。
3 计算分析
3.1 工程背景
连续刚构桥梁损伤指数的计算以某二级公路特大桥为例。该桥主跨跨径为190m,两侧边跨跨径均为103m,边中跨比为0.54,桥梁立面布置图如下。
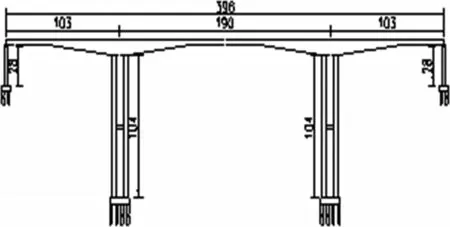
图1 某二级公路特大桥立面布置图(单位:m)
上部结构采用变截面箱梁,墩顶位置梁高为12m,中跨跨中及边跨支点位置梁高为3.8m;箱梁顶板宽度为12m,底板宽度为6.5m,混凝土强度等级为C55。下部结构采用等截面双肢薄壁墩,墩高为104m,中部设一道系梁;墩双肢中心距为10.5m,顺桥向肢宽3.5m,横桥向肢宽8.5m,混凝土强度等级为C50。主墩基础形式为嵌岩群桩基础。
当桥梁结构遭受强震作用时,其局部结构会呈现非弹性受力特点,而传统的反应谱分析法仅适用于弹性体系,不能考虑结构的弹塑性性质。为保证分析结果相对准确,本文采用时程分析法计算桥梁地震作用效应,时程曲线采用经调整的El-Centro波,分析时长取30s。
3.2 推倒分析结果
第一次推倒分析结果显示,该连续刚构桥梁在顺桥向的初始整体刚度为59713.4kN/m,横桥向的初始整体刚度分别为40792.5kN/m,屈服单元位置、屈服位移、最大位移反应及位移延性比的计算如表1所示。

表1 桥梁位移延性比计算表

横桥向4 41 42 43 44 85 86 87 88 41 42 43 44墩底系梁系梁系梁系梁墩顶墩顶墩顶墩顶系梁系梁系梁系梁2.221×10-3 3.902×10-4 4.360×10-4 1.184×10-3 6.952×10-4 1.708×10-3 1.842×10-3 1.733×10-3 1.907×10-3 2.394×10-4 2.391×10-4 2.394×10-4 2.393×10-4 5.651×10-3 1.280×10-2 1.304×10-2 1.262×10-2 1.289×10-2 2.712×10-3 2.526×10-3 3.212×10-3 2.938×10-3 2.783×10-3 2.806×10-3 2.436×10-3 2.439×10-3 2.544 32.804 29.908 10.659 18.541 1.589 1.371 1.854 1.541 11.625 11.736 10.775 10.192方向 屈服单元号屈服单元位置屈服位移(rad)最大位移反应(rad)位移延性比
根据表1的计算结果,按(2)式对第一次推倒分析中已屈服单元的刚度进行修正,并对经刚度修正的计算模型进行再次推倒分析。根据刚度修正后的推倒分析结果,该连续刚构桥梁在顺桥向的整体刚度为30876.3kN/m,横桥向的整体刚度为40627.5kN/m。
3.3 损伤指数的计算
根据(1)式分别计算该连续刚构桥梁在既定地震作用下顺桥向、横桥向的损伤指数如下:

桥梁损伤程度与损伤指数间的关系[6]如下:损伤指数在0至0.15 间时,桥梁轻微破坏,不经修复即可继续使用;损伤指数在0.15~0.3间时,桥梁中等破坏,经简单修复可继续使用;损伤指数在0.3~0.8间时,桥梁严重破坏,但经临时加固后可供应急使用;损伤指数大于0.8 时,桥梁倒塌。因此,该连续刚构桥梁在既定地震作用下严重破坏但并未倒塌,经临时加固后可供应急使用。
4 结论
(1)根据确定的桥梁损伤程度评价标准,可采用基于二次推倒分析的刚度退化模型,计算连续刚构桥梁在既定地震作用下的损伤指数,进而评价连续刚构桥梁的抗震能力。
(2)使用基于推倒分析的刚度退化模型计算连续刚构桥梁在既定地震作用下的损伤指数,具有概念明确、计算简便、易于工程应用等特点。
(3)为准确模拟连续刚构桥梁在地震作用下的惯性力分布,推倒分析的侧向荷载模式可采用基于特征值分析的振型荷载。
