基于应力-渗流-损伤耦合模型的重力坝三维水力劈裂数值模拟

沙 莎，张国新

（1.中国电建集团 北京勘测设计研究院有限公司，北京 100024；2.流域水循环模拟与调控国家重点实验室 中国水利水电科学研究院，北京 100038）

1 研究背景

随着我国水资源开发需求的增长以及筑坝技术的发展，修建200～300 m的超高坝早已成为现实，混凝土高坝的安全问题成为坝工界一个备受关注的重要课题。由于混凝土材料抗拉强度较低，大体积混凝土坝施工期极容易产生裂缝，尤其是碾压混凝土坝，还存在薄弱层面，这些裂缝和薄弱面在库水压力作用下是否会发生高压水劈裂是一个亟需研究的问题。国内外已有几座重力坝出现了高压水劈裂的现象，例如：加拿大的雷威尔斯托克坝、美国的德沃歇克坝和卢塞尔坝，施工过程中虽然采用了预冷骨料、水管冷却、表面保温等综合温度控制措施，坝体上游面仍出现了表面裂缝，水库蓄水后经过一段时间，表面裂缝突然大范围扩大，发展为劈头裂缝，深入坝内几十米，有的甚至将整个坝段一分为二，引起严重漏水［1］。我国柘溪［2］、桓仁［3］大头坝，玉石［4］、观音岩碾压混凝土重力坝也出现了同样的问题。因此，对混凝土重力高坝或超高坝进行安全评估时，考虑高压水劈裂作用的影响是非常重要的。

目前，在混凝土高压水劈裂的试验研究方面，已有学者进行了相关研究。Brühwiler和Saouma［5-6］研究了不同级配的混凝土裂缝内的水压分布变化规律及裂缝中静水压力对混凝土表观断裂能、表观断裂韧度的影响。Slowik和Saouma［7］研究了裂缝边缘张开速度不同时裂缝内水压分布随时间的变化以及裂缝突然闭合时对水压分布的影响。王建敏［8］采用大型尺寸楔入式紧凑拉伸试件进行了水力劈裂试验，研究了裂缝内的静水压力对断裂性能的影响，指出随着水压力的增加，试件所能承受的最大荷载减小。贾金生等［9］提出了全级配混凝土试件单轴拉、压应力作用下高压水劈裂模拟试验新方法，并推导了判定重力坝坝踵是否会发生水力劈裂的分析公式。通过试验可以揭示水力劈裂的机理，但是由于试验中采取的试件均是立方体、圆柱体试件，所以试验不能真实反映混凝土坝的形态及其受力条件，也无法预测裂缝扩展范围及危险程度。鉴于试验的不足，很多学者致力于混凝土坝高压水劈裂的数值研究。陈胜宏等［10］采用有限元法研究了高压水劈裂对小湾高拱坝坝踵开裂的影响，指出考虑高压水劈裂坝踵裂缝扩展范围比不考虑时大。Barpi和Valente［11］对混凝土重力坝建基面处裂纹的水力劈裂进行了模拟研究，讨论了断裂过程区的发展对裂缝内水压的影响。董玉文等［12］采用扩展有限元法进行了向家坝坝踵水力劈裂的数值分析，将裂缝面上的水压力视为均布荷载。王克峰等［13］采用扩展有限元法研究了考虑流固耦合效应的重力坝的水力劈裂问题。Secchi and Schrefler［14］基于分离裂缝模型和三维自动网格重构技术提出一种模拟饱和孔隙介质三维水力劈裂的方法，并且用于混凝土重力坝在水头超载作用下坝踵的开裂分析。

水力劈裂是个复杂问题，涉及到四个耦合过程：（1）裂纹面上水压力引发的介质变形；（2）裂纹内及周围介质中流体流动；（3）裂纹的扩展；（4）裂纹内的水渗透到周围介质中［15］。上述混凝土坝高压水劈裂的数值研究中，只有文献［14］考虑了这4个耦合过程。文献［10］和［12］将裂缝面上的水压力视为均布荷载，没有考虑裂缝扩展过程中水体流动引起的裂缝内的水压重分布。文献［11］和［13］则假定裂缝面是不透水的，且没有考虑周围介质中流体流动。已有的重力坝水力劈裂的数值研究大多是二维的，三维方面的十分罕见，特别是重力坝劈头裂缝方面的。

目前模拟水力劈裂的数值方法有：相场法［16］，近场动力学［17］，元胞自动机法［18］，离散元法［19］，流形元法［20］，无单元法［21］，有限元法［14］，边界元法［22］等。有限元法是最成熟，应用最广的数值方法，其本质上是一种连续介质力学方法，必须加以改进才能被用来分析裂缝扩展这样的不连续问题，改进的方法分为两类：变网格法和固定网格法。变网格法随着裂缝的产生，需要不断地重新划分网格，裂纹面必须与单元边保持一致，在裂尖区域需要细化单元或改用特殊形式的缝端奇异元，产生极大的前处理工作量。固定网格法则是保持网格不变，通过修改开裂单元插值关系、本构关系反映裂缝的存在，比如扩展有限元（XFEM）、连续损伤模型。相比较而言，固定网格法的应用更为方便。本文基于有限元采用一种各向同性损伤模型进行水力劈裂的模拟，将混凝土视为饱和的孔隙介质，根据孔隙介质有效应力原理，提出一种应力-渗流-损伤耦合模型，考虑水力劈裂过程中的耦合效应。采用该耦合模型，对国内某重力坝上游面垂直裂缝水力劈裂进行数值模拟。

2 应力-渗流-损伤耦合模型

假定大坝混凝土是饱和的孔隙介质。应力-渗流-损伤耦合模型包括了以下非线性行为：（1）单元损伤后的应力-应变关系；（2）损伤引起的孔隙水压影响系数的改变；（3）应力、损伤引起的单元渗透系数的改变。计算中假定受压时，应力应变关系是线弹性的，因为重力坝压应力一般不会超过其抗压强度。以下介绍这种耦合模型的特性。

2.1 损伤模型 混凝土的断裂特性表现为在真实的缝端前面存在一个断裂过程区，在断裂过程区中，通过骨料的咬合和界面间的摩擦力，相互之间仍有应力作用，断裂过程区的存在使得混凝土呈现出应变软化特性。由Hillerborg等［23］提出的虚拟裂缝模型可以很好地模拟断裂过程区的力学特性。目前，关于混凝土拉伸曲线的数学表达式，大多数学者主张上升段采用直线，主要区别在下降段，包括：单直线下降、分段下降、曲线下降。但无论采用何种形式，均应保持拉伸曲线的断裂能相同［24］。本文下降段采用由江见鲸［24］提出的指数下降型表达式。因此，单轴受拉条件下，应力-应变关系表达为：

式中：E0为材料无损时的弹性模量；ft0为抗拉强度；εt为单元的单轴拉伸应变；ε0为开裂时的应变，ε0=ft0/E0；α为控制下降段的软化系数。

断裂能GF的含义如图1所示，为应力-裂缝宽度曲线与坐标轴围成的面积，可表达为式（2）；单位开裂宽度的断裂能gf的含义如图2中阴影所示，为应力-应变曲线下降段与ε=ε0、横坐标轴ε围成的面积，可表达为式（3）。

图1 应力-裂缝宽度曲线和断裂能Gf

图2 单位开裂宽度的断裂能gf

式中：w为过程区内所有微裂缝张开的位移量之和，h为混凝土微裂缝分布区宽度。

根据式（1）

断裂能GF与单位开裂宽度的断裂能gf存在如下关系：

式中：lt为混凝土单元特征尺寸。对于平面单元，取积分点区域面积的平方根；对于实体单元，取积分点区域体积的立方根。

由式（4）、式（5），本构曲线下降段的软化系数应满足

根据Lemaitre［25］提出的等效应变原理，假定Cauchy应力σ作用在受损材料上的应变与有效应力作用在无损材料上的应变等价，即

得到

式中：E0为材料无损时的弹性模量；为材料受损后的弹性模量；d为损伤变量，d=0对应于无损伤状态，d=1对应于完全损伤状态，0＜d＜1对应于不同程度的损伤状态。

从损伤力学的角度看，岩石、混凝土宏观应力-应变的非线性，是由于其受力后不断损伤引起的微裂纹萌生和扩展造成的。这种脆性在拉伸作用下更加明显，因此采用弹性的损伤力学本构方程来描述其力学特性是合适的。经过研究和实验证明，采用弹塑性损伤本构模型模拟的结果和弹性损伤本构模型的结果相差不大［26］。因此，本文采用弹性损伤模型进行计算。

由式（1）、式（8），单轴拉伸作用下，混凝土损伤演化方程可表示为：

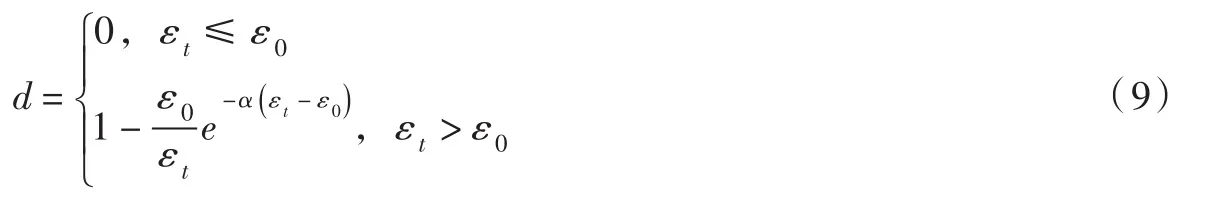
2.2 孔隙介质有效应力原理 有效应力概念应用于被单相流体浸润的岩石、混凝土材料，可以看成太沙基有效应力原理应用于土体的推广。基于有效应力原理，Biot首次引进一个标量参数，即Biot系数，反映孔隙水压对有效应力的影响（Biot，1941，1955，1977）［27-29］。在文献［28］中，孔隙率 bi被定义为有效孔隙面积与横截面Ai的比值。有效孔隙面积则被定义为在垂直于横截面Ai的方向，单位长度所有微小孔隙面积的总和。孔隙率bi同样可以代表孔隙体积（Vp）与代表体体积（Vb）的比值。在混凝土坝弹性分析中，通常假定含有孔隙的大坝混凝土是均质、各向同性的，因而经常采用bi的一个各向同性值bx=by=bz=b0进行混凝土坝的弹性分析。对于土体的应力计算，通常取b0≈1。然而，对于弹性范围内混凝土的应力计算，取b0≈1则是不合理的，因为混凝土即使在即将破坏的状态下，b0仍小于1。

图3 饱和孔隙介质的应力分解

文中应力符号以拉应力为正。饱和孔隙介质的应力分解如图3所示，作用在单元表面的总应力可以分解成两部分：与内部水压力p相互平衡的外力bp和有效应力，单元的平均变形只与有效应力有关，可表示为：

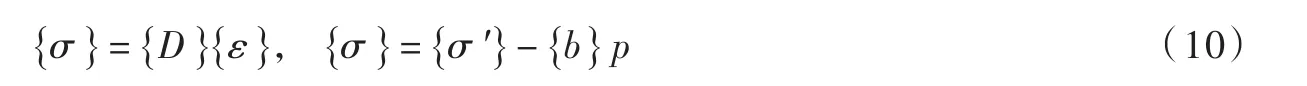
2.3 孔隙水压影响系数与损伤关系 单元未损伤时假定bx=by=bz=b0，单元损伤后，垂直于裂缝方向的孔隙水压影响系数与平行于裂缝方向孔隙水压影响系数理应是不一样的。图4定性的展示了开裂对孔隙水压影响系数的影响，1、2、3分别代表第一、二、三主应力的方向，建立以主应力方向为坐标轴的局部坐标系。开裂对垂直于裂缝面方向的b1影响较大，b2和b3在一个范围内，即b0＜b2=b3＜b1［30］。Bary and Bournazel［31］通过实验得出了一个各向异性的Biot张量，其与各个方向的损伤值和孔隙水压有关。由于缺乏开裂对平行于裂缝方向的孔隙水压影响系数影响的试验资料，本文假定混凝土损伤之后，孔隙水压影响系数仍各向同性，即b1=b2=b3。弹性状态下，b1=b2=b3=b0，b0为初始Biot系数；完全损伤后，b1=b2=b3=1，孔隙水压影响系数随损伤的演化方程可表示为：

2.4 渗透系数与应力及损伤关系 混凝土在微观上是由骨架和孔隙组成的，这种构造特征使得其在受荷载或扰动作用后，其微观几何形态、孔隙的结构发生改变，从而导致孔隙率和渗透性发生改变。孔隙率的变化主要由两部分组成：一是由于结构形变引起孔隙体积变化；二是微裂纹等缺陷的萌生、扩展及贯通，使得材料内部的孔隙结构和大小发生改变，即材料发生损伤而引起的孔隙结构变化［32］。

当单元未发生拉损伤，处于弹性状态，即损伤变量d=0时，渗透系数与有效应力成指数关系，表示如下：

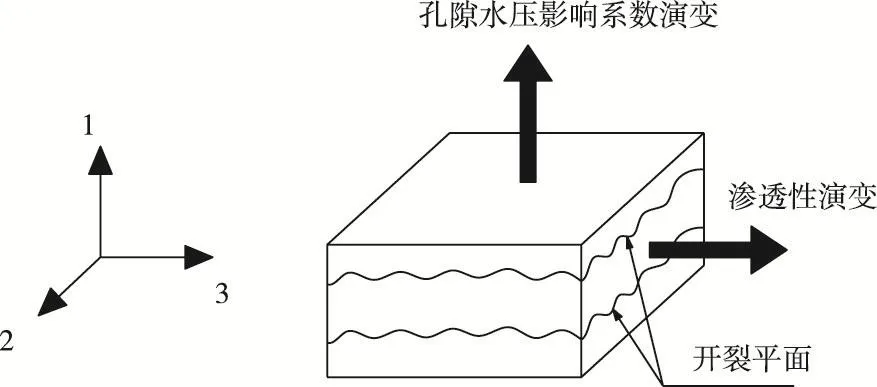
图4 开裂对孔隙水压影响系数及渗透性的影响

式中：k0为初始渗透系数；a0为耦合系数；σ1、σ2、σ3为有效主应力，以受拉为正；k11、k22、k33为方向与有效主应力一致的主渗透系数。

当单元第一主应力达到抗拉强度，发生损伤，即损伤变量d＞0时，单元中产生裂缝，图4定性地展示了开裂对单元渗透性的影响。混凝土中的水主要沿着裂缝流动，方向2、方向3的渗透系数大大提高，此时近似按照裂隙渗流考虑，采用在裂隙渗流研究中运用得最为广泛的单裂隙平行板水力模型，则渗透系数表示如下：

式中：u为裂缝张开的宽度，近似按u=（ε1-εt）lt计算，εt、lt的定义见2.1节；υ为水的运动黏滞系数，g为重力加速度。由k11、k22、k33形成局部坐标系下的渗透矩阵［k′］，经坐标转换将其转换到整体坐标系中，则整体坐标系下的渗透矩阵［k］可表示为：

2.5 渗流场基本微分方程 假定水不可压缩，根据Darcy定律，可得无源非稳定情况下渗流连续方程：

式中：S为饱和度，H为水头势，kij为渗透系数张量；

对于非恒定渗流，其定解条件包括如下边界条件和初始条件：

水头边界：

流量边界：

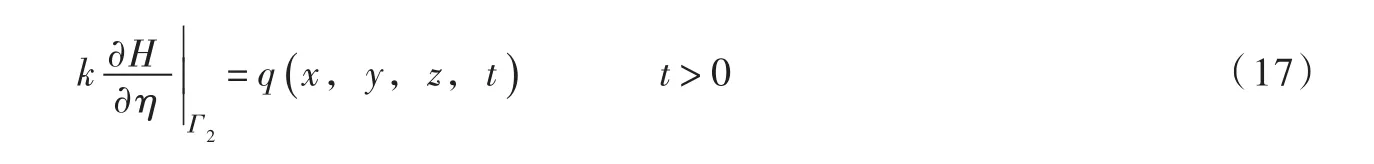
隔水边界：

初始条件：

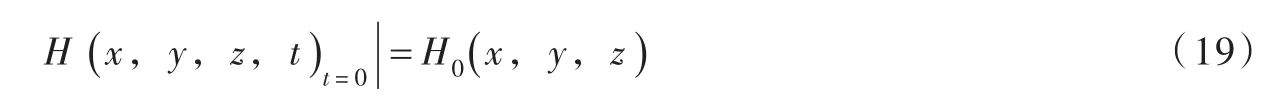
式中：f为已知水头边界值，q为已知流量边界，H0为已知函数。

如果按照恒定渗流计算，即式（15）的右侧为0，没有初始条件式（19）。

2.6 程序实现 SAPTIS软件是中国水利水电科学研究院结构材料所独立开发的大型结构多场仿真与非线性分析软件，该软件具备混凝土坝温度、渗流、变形、应力等多场耦合仿真分析功能［33-35］。本文在SAPTIS原有功能基础上加入了应力-渗流-损伤耦合非线性功能，进行水力劈裂的数值模拟计算。

3 实验验证

为了验证本文应力-渗流-损伤耦合模型的正确性，对贾金生等［9］做的圆柱体混凝土试件水力劈裂试验进行了数值模拟，试件尺寸及受力条件如图5所示，本文计算模型如图6所示。选取文献［9］中3个试件进行数值模拟，试件力学参数、受力状态与文献［9］一致，见表1。水压加载过程与文献［9］一致，如图7所示，即采用梯级加载方式，水压小于1.0 MPa时，每小时增加0.5 MPa；水压1 MPa至2 MPa时，每小时增加0.2 MPa，水压大于2 MPa时，每小时增加0.1 MPa。渗流场计算按照非恒定渗流考虑，混凝土渗透系数k0=5×10-9m/s，耦合系数a0=0.01。

图5 高压水劈裂试验原理（单位：mm）

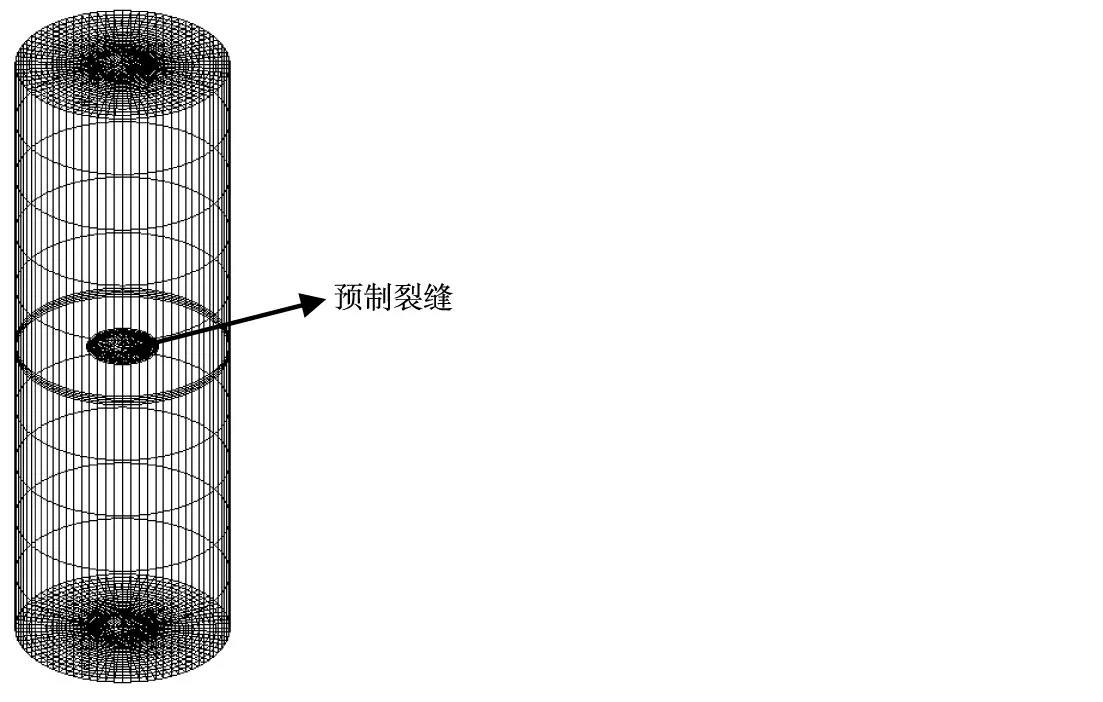
图6 计算模型

表1 圆柱体混凝土试件力学参数及受力状态

试件Ⅳ发生水力劈裂破坏时的损伤分布如图8所示，由图8可以看出，试件损伤区域几乎和预制缝平行。不同水压作用下，试件Ⅳ预制缝所在截面损伤分布如图9所示，孔隙水压分布如图10所示。由图9可知，水压1.4 MPa，缝端开始损伤，随着水压的增加，损伤区域越来越大，水压3.4 MPa，损伤区域面积占总面积55%，与文献［9］描述的劈裂面积十分接近，水压超过3.4 MPa，截面全部损伤，本文认为水压3.4 MPa时，试件发生了水力劈裂破坏。由图10可以看出，随着水压增加，最大孔隙水压分布区域逐渐增大，其边界与图9中损伤区域的边界十分吻合，这是由混凝土单元损伤之后，渗透系数显著增加，水不断渗入引起的。不同试件水力劈裂水压的试验值、计算值见表2，计算值与试验值吻合很好，可以看出，本文耦合模型可以很好地模拟水力劈裂现象。

4 国内某重力坝水力劈裂数值模拟

图7 水压加载过程

图8 P=3.4MPa，试件损伤分布

图9 不同水压作用下，预制缝所在截面损伤分布等值线图

该水电站为西南某水电基地的中游河段，水库正常蓄水位1134 m，库容约20.72亿m3。施工过程中，16号坝段上游面出现了表面裂缝，蓄水过程中这些表面裂缝扩展为劈头裂缝。本文以16号坝段为研究对象，在其上游面设置了一个竖直的初始缝面，模拟了其在蓄水过程中的水力劈裂现象。该坝段坝顶高程1139 m，建基面高程990 m，坝体及坝体-地基模型如图11所示，模型中考虑了坝体排水、廊道、地基排水、帷幕。由于缺乏施工期形成的表面裂缝的形状、范围，本文假定初始裂缝面形状为三角形，底高程1005 m，顶高程1025 m，最大深度为5 m。坝基的计算范围为向上游、下游和基岩深度方向各取1.5倍坝高，坝基底边界为竖向约束，四个侧边界均为水平约束。

计算中考虑的荷载为自重、上下游水荷载，先施加自重荷载，再施加水压力，上游水位按每荷载步增加10 m的方式从1020 m抬升至1120 m，最后一个荷载步水位从1120 m抬升至正常蓄水位1134 m，下游水位1010 m保持不变。坝体混凝土、地基力学特性见表3。渗流场计算按照恒定渗流考虑，混凝土渗透系数k0=5×10-9m/s，耦合系数a0=0.01。

不同水位坝体损伤分布如图12所示。由图12可以看出，（1）蓄水至1070 m时，坝体出现损伤；（2）随着水位增加，损伤区域从裂缝面尖端逐步向坝体上部、内部、下部扩展；（3）水位从1070 m上升至1110 m过程中，损伤区域缓慢扩展，从1110 m上升至1120 m，损伤区域明显增大，向内部扩展至坝体排水管处；（4）水位由1120 m上升至正常蓄水位1134 m时，损伤区域显著增大，上部达到高程1060 m处，下部达到高程992 m处，最大裂缝深度33 m，最终裂缝面呈圆弧状。

图10 不同水压作用下，预制缝所在截面孔隙水压分布等值线图（单位：m）

表2 水力劈裂水压计算值、试验值对比

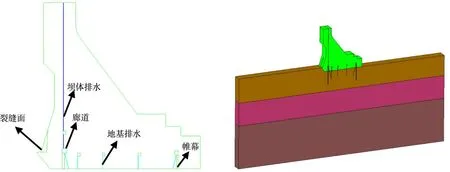
图11 坝体、坝体-地基模型

表3 国内某重力坝材料参数

图12 不同水位坝体损伤分布等值线

设计院根据安全监测实测结果得到的正常蓄水位下的裂缝范围如图13所示。由图13可以看出，正常蓄水位下，裂缝范围上部达到高程1070 m处，底部达到高程997 m处，裂缝向坝体内部扩展的最大深度达到40 m左右。比较图12（f）及图13可以看出，本文数值模拟得到的正常水位下裂缝的扩展范围与设计院根据安全监测实测结果得到的范围基本吻合，设计院的裂缝范围比本文向内部扩展的更深一点，向上扩展的更高一点。经过初步分析差异主要与初始裂缝面形状、范围，坝体力学特性参数，蓄水过程等有关，计算中当初始裂缝面的最大深度增加时，正常水位下裂缝扩展范围增大，坝体抗拉强度降低时，正常水位下裂缝扩展范围也增大，所以掌握真实的初始裂缝面形状、范围，坝体力学特性参数，蓄水过程等资料是采用本文耦合模型准确预测裂缝是否扩展、扩展过程、最终扩展范围的关键。

图13 裂缝预估范围

5 结论

本文提出了一种应力-渗流-损伤耦合模型，并用于混凝土重力坝三维水力劈裂的模拟。

该耦合模型具有以下特点：（1）考虑了混凝土断裂过程区的应变软化特性；（2）基于断裂能守恒原理将损伤模型与断裂力学相结合，使得断裂能的消散不会受到网格大小的影响；（3）考虑了水力劈裂过程中的4个耦合过程。

采用该耦合模型，对内置裂缝的圆柱体试件的水力劈裂进行了数值模拟，水力劈裂水压的计算值与试验值吻合很好，验证了所提耦合模型的合理性。

在此基础上，进行了国内某混凝土重力坝三维水力劈裂的模拟：（1）蓄水至1070 m时，坝体出现损伤；（2）随着水位增加，损伤区域从裂缝面尖端逐步向坝体上部、内部、下部扩展，蓄水至正常蓄水位1134 m，损伤区域上部达到高程1060 m处，下部达到高程992 m处，最大裂缝深度33 m，最终裂缝面呈圆弧状；（3）数值模拟得到的损伤区域与设计院根据安全监测实测结果得到的范围基本吻合。研究结果表明：采用该耦合模型可以十分便捷有效地进行混凝土重力坝三维水力劈裂的模拟，评估表面裂缝的危险程度。然而水力劈裂是一个复杂的问题，损伤对孔隙水压影响系数、渗透系数的影响还需要进一步研究。