高空风场对某飞行器级间分离影响研究

于峰，赵志博，刘文一

高空风场对某飞行器级间分离影响研究

于峰1，赵志博2，刘文一1

（1.91550部队41分队，辽宁 大连 116023；2. 91049部队，山东 青岛 266102）

研究高空风场对飞行器飞行时级间分离的影响。建立飞行器分离模型，仿真计算飞行器分离时下面级的横移距离、两个关键部件之间的间隙。在最低飞行条件风速34 m/s时，下面级横移距离和两个关键间隙均满足设计条件。在仿真计算风速40 m/s条件下，下面级横移距离、两个关键部件间隙均满足设计要求，因此最低飞行条件风速可放宽至40 m/s。在最大风速45 m/s时，三个值均超出了设计值，有可能会对分离造成影响。高空风对飞行器级间分离存在一定影响，随着高空风风速的增加，面级的横移距离和两个关键部件之间键间隙随之增加。

高空风；分离；横移；间隙

飞行器飞行时必须要经历属于四维空间的高空风场，因此飞行器设计时既要考虑最大风，也要考虑风切变，既要考虑其空间变化，也要考虑其时间变化[1]。飞行器在级间分离时，一方面风使下面级分离体发生了相对运动，另一方面风从飞行器头部到尾部有大小变化[2]。这些因素对飞行器的飞行和分离会产生较大影响，因此有必要对其进行分析，以避免高空风场对飞行器正常飞行造成影响。

1 高空风场模型

高空风对飞行器的影响主要是气动载荷，它取决于动压和俯仰角。高空风对飞行器有四种物理作用：风载荷、风切变、风振和阵风干扰。高空风往往是以两种以上的效应作用于飞行器，从而对飞行器的影响更大[3]。

1.1 气动载荷

气动载荷可以用动压和俯仰角的乘积来表示。当风运动遇到障碍物时，单位体积的动能施加于障碍物上的压力为动压。当风以一定速度被滞止时，压力增大，在等熵条件下，将全部转化为动能[4]。动压的表达式为[5]：

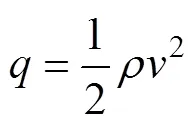
飞行器飞行时，1为飞行速度，2为风速，=v+v，代入式（1）得：

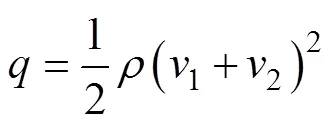
当1≥2时，2可以忽略。

1.2 风载荷

风载荷指风吹过障碍物时，障碍物在垂直于风速方向上单位面积所受到的压力。风压是两部分作用之和：一是障碍物迎风面的动压，二是障碍物背风侧的压降。压降的表达式为：

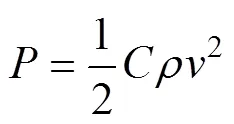
式中：为结构常数，对于圆柱形障碍物，=0.3。将动压和压降作用加起来，得到风压的表达式[6]：

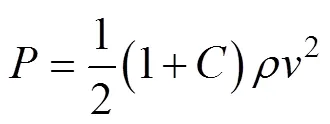
1.3 风切变

风切变为某一方向上任何风分量和风矢量的局地变化，通常用表示风矢量，、、分别表示、、方向的风分量[7]：

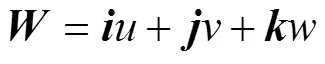
式中：、、分别为指向、、的单位矢量。飞行器飞行受到的风切变的影响，可通过建立在飞行器上的坐标系来表达。参照拉格朗日座标，飞行器飞行时的风速变化可由式（6）给出：

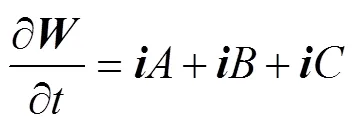
是,的函数，式（7）又可变为：

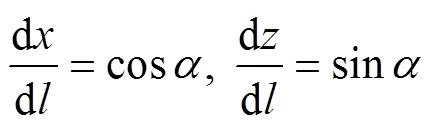
式中：表示矢量的仰角[8]。

将式（8）代入式（7），整理后得到[9]：

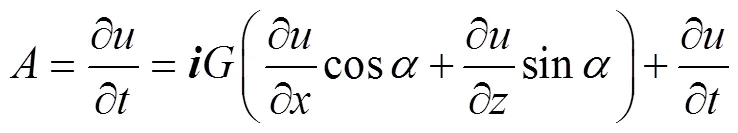
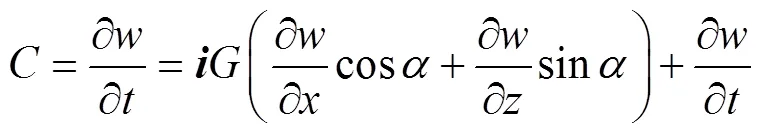
1.4 风振

当风吹过飞行器时，在飞行器的背风侧会产生卡曼涡旋。卡曼涡旋会使飞行器在垂直于风的方向上发生振动，这种现象为风振[10]。这种振动往往会使飞行器发生结构性破坏，当风振与飞行器发生共振时产生的破坏力更大[11]。

当飞行器在高空风场中飞行时，可将其看作是一个圆柱，其自振周期为[12]：

式中：为飞行器长度；为飞行器外径。

2 仿真模型

2.1 物理模型

一个完整的仿真模型包括几何模型、约束类型、初始运动值和受力等[13]。某飞行器上面级发动机喷管套在下面级前连接裙里，其模型如图1所示。深色部分为上面级，浅色部分为下面级，同时标出了两个关

图1 仿真模型

键件的位置、高空风方向和下面级横移方向。

对于飞行器的上面级和下面级，都有6个拉格朗日方程及其对应的约束方程[14]：

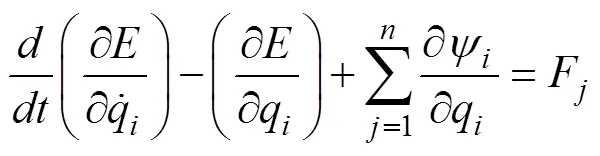
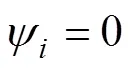
将方程（13）和方程（14）改写成矩阵型：

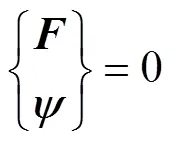
式中：0表示零矩阵；为广义力矩阵；为约束方程矩阵[16]。

在广义坐标下，动能可以用式（16）表示：

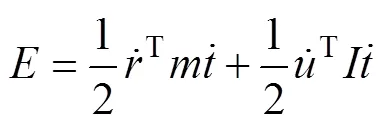
式（15）与式（16）合并为：

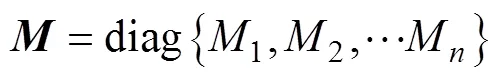
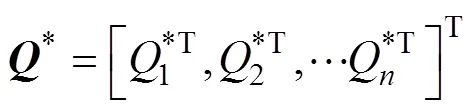
方程（18）、（19）均为代数-微分方程。在进行多体动力学分析时，可将拉格朗日方程写为一阶微分方程形式，且引入[18]：

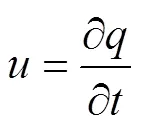
得到：

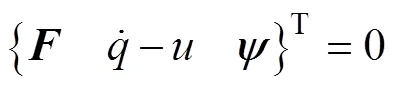
2.2 初始运动

飞行器有一个初始速度，计算时需要设置初始速度在参考坐标系上的分量值[19]，建立的坐标系如图2所示。

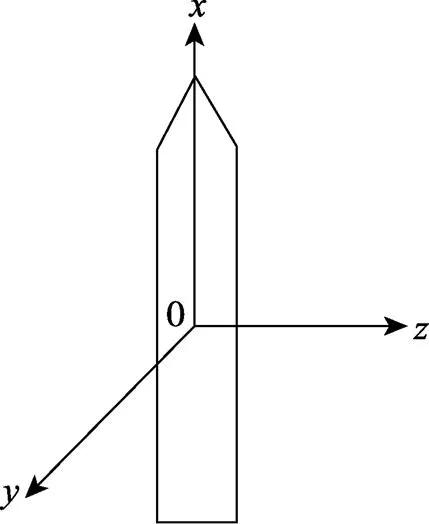
图2 坐标系

飞行器在级间分离时刻，其速度矢量为：

2.3 内力载荷

飞行器分离时，上、下面级之间存在约束，因此上、下面级之间成对出现大小相等、方向相反的内力[20]。对飞行器分离不做功的内力为保守内力，对飞行器分离做功的内力称为非保守内力。飞行器分离，受到外来载荷或非保守内力作用时，飞行器的上、下面级就会产生加速度，飞行器分离模型就会处于动态变化中[21]。

3 仿真计算及结果分析

3.1 计算条件

计算模型采用三维六自由度刚体运动学和动力学模型，考虑的受力工况主要有：下面级和上面级主发动机推力、高空风场产生的气动载荷、分离时上面级和下面级的速度、质量特性等[22]，见表1。飞行器飞行时具有一定攻角，计算时只考虑风载荷垂直加载在飞行器迎风面的分量[23]。

表1 级间分离时飞行器载荷

Tab.1 Load of aircraft during stage separation

3.2 计算结果

仿真计算了飞行器上下面级之间分离后，不同风速条件下，下面级的横移距离、关键间隙1、2的距离。

3.2.1 下面级横移距离

飞行器上下面级之间分离后，风速分别为27、30、34、38、40、45 m/s时，下面级的横移距离如图3所示。

3.2.2 关键间隙1距离

飞行器上下面级之间分离后，风速分别为27、30、34、38、40、45 m/s时，关键间隙1距离如图4所示。

3.2.3关键间隙2距离

飞行器上下面级之间分离后，风速分别为27、30、34、38、40、45 m/s时，关键间隙2距离如图5所示。

图3 不同风速时下面级的横移距离

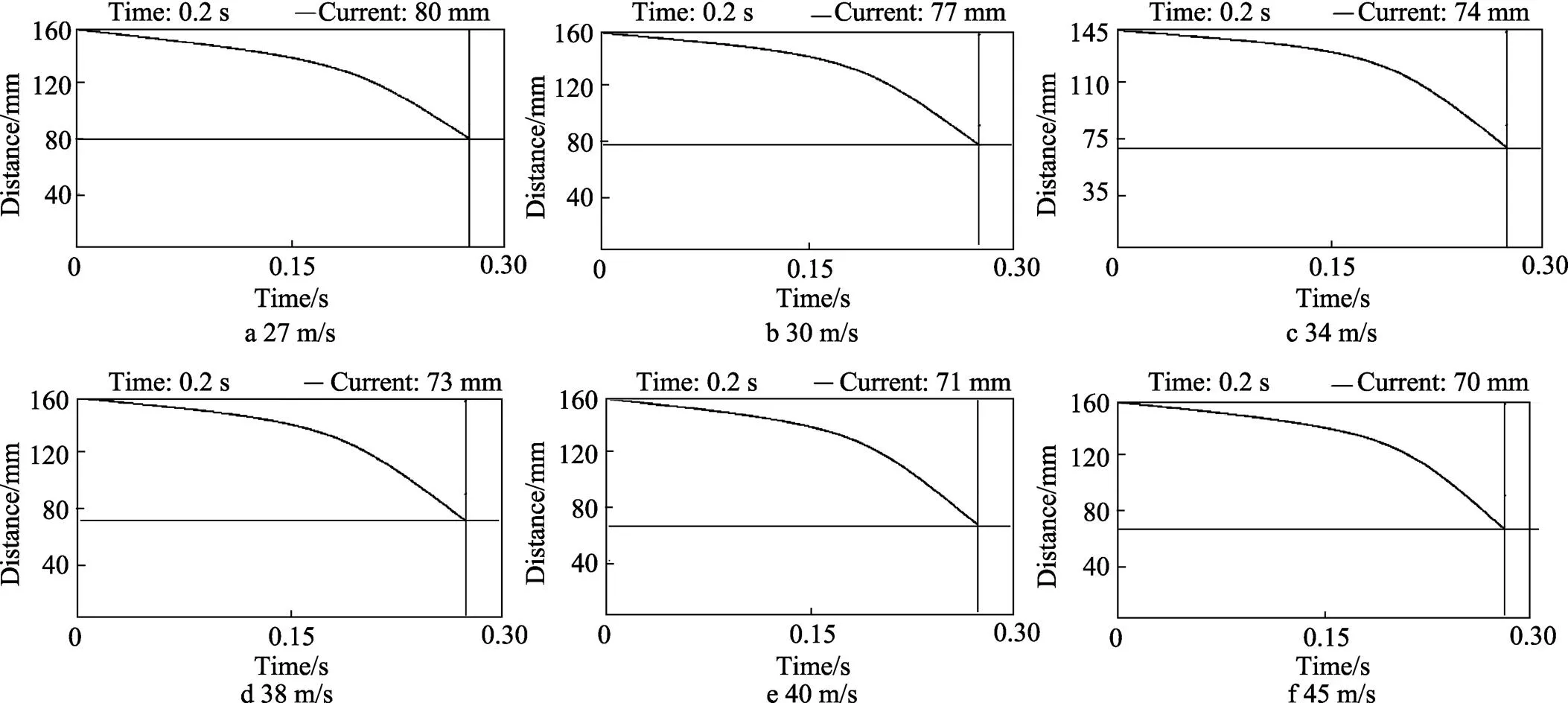
图4 不同风速时关键间隙1距离

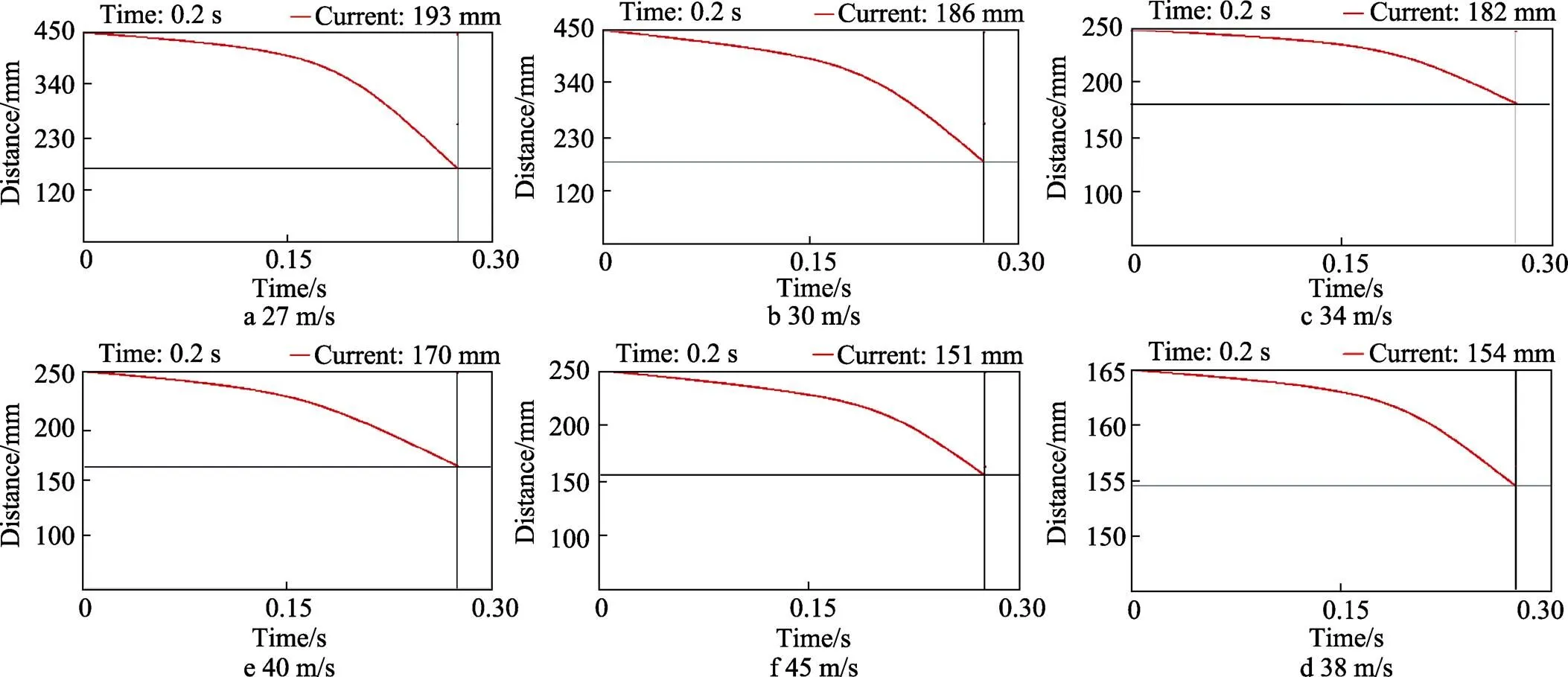
图5 不同风速时关键间隙2距离

3.3 结果分析

仿真计算结果表明，高空风对飞行器分离存在一定影响。随着高空风风速的增加，飞行器下面级的横移距离随之增加，关键间隙值1和2随之减小，见表2。设计值要求分离时下面级最大横移距离为31 mm，关键间隙1的最小值为69 mm，关键间隙2的最小值为152 mm。

表2 风速增加与下面级横移距离、两个关键间隙值之间的关系

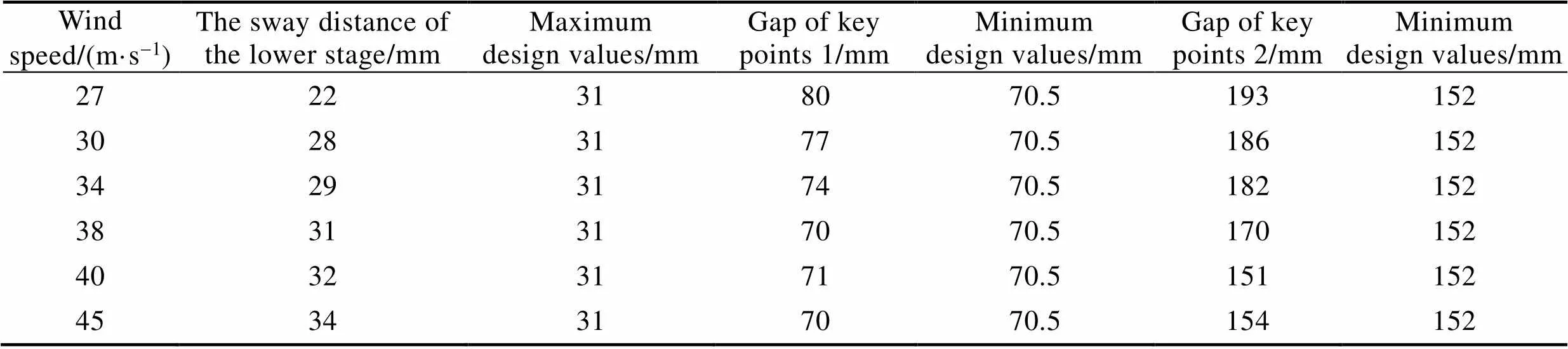
Tab.2 The relationship among the increased wind speed, sway distance of the lower stage and gaps of two key points

4 结论

为了研究高空风场对飞行器飞行时级间分离的影响，建立了飞行器分离模型，仿真计算了飞行器分离时下面级的横移距离和两个关键部位之间的间隙，得出以下结论。

1）高空风对上面级和下面级分离存在一定影响，随着高空风风速的增加，下面级的横移随之增加，使危险点之间的间隙随之减小，会对级间分离和飞行器正常飞行带来影响。

2）在最低飞行条件高空风速34 m/s时，下面级横移距离为29 mm，两个关键间隙分别为73 mm和182 mm，均满足设计条件。

3）在计算风速40 m/s条件下，下面级横移距离、两个关键部件间隙均满足设计要求，因此最低飞行条件可放宽至40 m/s。

4）在计算最大风速45 m/s条件下，关键间隙1减小至63 mm，关键间隙2减小至140 mm。这两个间隙均偏小，有可能会对飞行器级间分离和正常飞行造成影响。

[1] 李臣明, 张微, 韩子鹏. 100 km以下风场对远程弹箭运动的影响研究[J]. 兵工学报, 2006, 28(10): 1170-1173. LI Chen-ming, ZHANG Wei, HAN Zi-peng. Effect of Wind Field at High Altitude Under 100 km on Long-range Shells and Rockets[J]. Acta Armamentarn, 2006, 28(10): 1170-1173.

[2] KELLY J M, PIETER G B, BANDU N P, et al. Overview of TRANSONIC to Hypersonic Stage Separation Tool Development for Multi Stage to Orbit Concepts[R]. AIAA 2004-2595, 2004.

[3] 美国国家海洋和大气局､国家航宇局和美国空军部.标准大气(美国1976)[M]. 北京: 科学出版社, 1982. National Ocean and Atmosphere Bureau of America, NationalSpace Navigation Bureau and America Air Force Office. Standard Atmosphere(US,1976)[M]. Beijing: Science Pros,1982.

[4] 马瑞平, 廖怀哲. 中国地区20~80 km高空风的一些特征[J]. 空间科学学报, 1999, 19(4): 334-341. MA Rui-ping, LIAO Huai-zhe. The Characteristics of Winds at Height of 20~80 km in the Chinese Area[J]. Chinese Journal of Space Science, 1999, 19(4): 334-341.

[5] GUNGLE R L, BROSIER W S, LEONARD H W. An Experimental Technique for the Investigation of Tipoff Associated with Stage Separation of Multistage Rocket Vehicles[R]. NASATND-1030, 1962.

[6] 刘文一, 杨春, 杨培源. 固体发动机金属材料和复合材料壳体水下力学特性分析[J]. 航天制造技术, 2017, 205(5): 47-49. LIU Wen-yi, YANG Chun, YANG Pei-yuan. Mechanical Property Evaluation of Solid Rocket Motor Case of Steel Material and Composite Material under Water[J]. Aerospace Manufacturing Technology, 2017, 205(5): 47-49.

[7] DE CASTRO L N, VON ZUBEN F J. The Clonal Selection Algorithm with Engineering Applications[C]// Proceedings of GECCO`00, Workshop on Artificial Immune Systems and Their Applications. Las Vegas, USA, 2000.

[8] KECHRIOTIS G I, MANOLAKOS E S. Hopfield Neural Network Implementation of Tile Optimal CDMA Multiuser Detector[J]. IEEE Transactions on Neural Networks(S1045-9227), l996, 7(1): 131-141.

[9] 刘文一, 焦冀光. 某飞行器复合材料薄壁加筋结构舱段稳定性分析[J]. 舰船电子境工程, 2016, 36(2): 110-113. LIU Wen-yi, JIAO Ji-guang. Stability Analysis of a Aircraft`s Thin-walled Reinforced Composite Material Cabin[J]. Ship Electronic Engineering, 2016, 36(2): 110-113.

[10] 牛跃听, 穆希辉, 姜志保. 某型火箭弹控制舱环境适应性研究[J]. 装备环境工程, 2014, 11(1): 86-92. NIU Yue-ting, MU Xi-hui, JIANG Zhi-bao. Research on Environmental Adaptability of a Guided Rocket[J]. Equipment Environmental Engineering, 2014, 11(1): 86-92.

[11] 刘文一, 焦冀光. 固体发动机装药热安全性数值分析[J]. 装备环境工程, 2016, 13(2): 130-131. LIU Wen-yi, JIAO Ji-guang. Numerical Analysis on the Thermal Safety of Solid Rocket Motor Propellant[J]. Equipment Environmental Engineering, 2016, 13(2): 130-131.

[12] 赵保平, 孙建亮, 蔡骏文, 等. 航天动力学环境的最新进展与技术展望[J]. 装备环境工程, 2015, 12(3): 8-14. ZHAO Bao-ping, SUN Jian-liang, CAI Jun-wen, et al. Recent Development and Prospect of Astrodynamic Environmental Technology[J]. Equipment Environmental Engineering, 2015, 12(3): 8-14.

[13] 李尧. 飞机温度环境适应性要求分析和确定技术探讨[J]. 装备环境工程, 2008, 5(6): 60-64. LI Yao. Analysis and Confirmation Techniques for Requirements of Temperature Environmental Worthiness of Aircraft [J]. Equipment Environmental Engineering, 2008, 5(6): 60-64.

[14] 刘文一, 李玉龙, 吴训涛. 基于分布水动压力的飞行器水下载荷计算方法研究[J]. 导弹与航天运载技术, 2019, 336(1): 20-23. LIU Wen-yi, LI Yu-long, WU Xun-tao. Calculation method of Underwater Load of Aircraft Based on Distributed Hydrodynamic Pressure[J]. Missiles and Space Vehicles, 2019, 336(1): 20-23.

[15] 刘章龙, 赵徐成, 胡涛. 基于高原环境的保障装备适应性技术研究[J]. 装备环境工程, 2016, 13(2): 35-36. LIU Zhang-long, ZHAO Xu-cheng, HU Tao. Adaptive Technology of Support Equipment Based on Plateau Environment[J]. Equipment Environment Engineering, 2016, 2016, 13(2): 35-36.

[16] SENOCAK I, SHYY W. A Pressure-based Method for Turbulent Cavitating Flow Computations[J]. Journal of Computational Physics, 2002, 176(2): 363-383.

[17] EDWARDS J R, LIOU M S. Simulation of Two-phase Flows Using Low-diffusion Shock-capturing Schemes[C]// 44th AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada, 2006.

[18] LEE C, BYUN D. Cavitation Flow Analysis of Axisymmetric Bodies Moving in the Water[J]. ICCSA LNCS, 2006, 3984: 537-545.

[19] CHEN Y, LU C J, GUO J H. Modeling and Simulation of Cavitating Flow over Underwater Vehicle with Large Angle of Attack [J]. Journal of Ship Mechanics, 2010, 14(12): 1319-1330.

[20] 李强兵. 基于L-M法的某型UUV系统可靠性评估及应用[J]. 机械, 2015, 42(5): 32-33. LI Qiang-bing. Comprehensive Evaluation of System Reliability and Application of a Certain UUV Based on L-M[J]. Machinery, 2015, 42(5): 32-33.

[21] 李玉杰, 石颜青, 罗振兵. 水滴结冰结霜及合成双射流的防霜防冰实验[J]. 气体物理, 2017, 2(5): 37-45. LI Yu-jie, SHI Yan-qing, LUO Zhen-bing. An Experimental Investigation on the Process of Droplet Icing/Forsting and Anti-frosting /Anti-icing Using Dual Synthetic Jet[J]. Physics of Gases, 2017, 2(5): 37-45.

[22] HAYASHI Y, AOKI A, ADACHI S, et al. Study of Frost Properties Correlating with Frost Formation Types[J]. Heat Transfer, 1997(99): 239-245.

[23] FEUILLEBOIS A, LASEK A, CREISMEAS P, et al. Freezing of a Subcooled Liquid Droplet[J]. Colloid Sci, 1995(169): 90-102.

Effect of High Altitude Wind Field on Stage Separation of an Aircraft

YU Feng1, ZHAO Zhi-bo2, LIU Wen-yi1

(1. Unit 41 of PLA 91550, Dalian 116023, China; 2. PLA 91049, Qingdao 266102, China)

The work aims to research the effect of wind field at high altitude on the stage separation of aircraft during flying. A stage separation model of aircraft was established. The sway distance of the lower stage and the gaps of two key points of aircraft after its stage separation were simulated. The sway distance of the lower stage and the gaps of two key points of aircraft all met the design conditions and requirements when the minimum wind speed and the simulated one were respectively 34 m/s and 40 m/s. Therefore, the minimum wind speed for flying could be relaxed to 40 m/s. When the maximum wind speed was 45 m/s, the sway distance and the gaps above all exceeded the design values, so the stage separation would be affected by it. It proves that the stage separation of aircraft will be affected by high altitude wind in some way, and the sway distance of the lower stage and the gaps of two key points of aircraft will be increased with the increase of high altitude wind speed.KEY WORDS: high altitude wind; separation; sway; gap

2019-09-06；

2019-10-02

10.7643/ issn.1672-9242.2020.03.018

V112.71；O358

A

1672-9242(2020)03-0108-06

2019-09-06；

2019-10-02

于峰（1967—），男，硕士，高级工程师，主要研究方向为武器装备鉴定。

YU Feng (1987—), Male, Master, Senior engineer, Research focus: weapons and equipment identification.