浅议小学数学中解决实际问题方法的发展

李蕊

[摘要]鸡兔同笼这个问题流传已久，解决方法层出不穷且难易不一。基于同阶段的学生解决这一问题的方法，来研究学生解决“鸡兔同笼”这一实际问题方法的发展，并对教学进行思考。

[关键词]鸡兔同笼;方法;思维

[中图分类号]G623.5 [文献标识码]A [文章编号]1007-9068（2020）08-0085-02

数学是一门逻辑性较强的学科，对于小学数学而言，数学的学习过程一定要有趣味性才能启发学生，并引导学生深入学习。单纯的学习概念或运算方法显得十分枯燥乏味，于是在小学数学中多了一类解决实际问题的题目，这类题目通常由文字或图形来表达一定的含义，学生通过读题来理解题意，并结合学过的知识来思考如何解决这一问题，整个过程不仅加强了学生对知识的理解，更让学生理解了数学与实际生活的联系。对于解决实际问题而言，学生在不同阶段解决问题的方法和形式不尽相同，可以说，随着数学学习的深入，学生的解题能力在慢慢提高，并形成更多新的方法和技巧，使自己的实际应用能力更加强。这篇文章的内容将会就小学生在不同阶段下解决实际问题方法的发展进行研究。

小学数学中，有一个非常经典的问题叫“鸡兔同笼”问题，源自中国古代数学著作《孙子算经》。它实质是一个方程问题，但在小学阶段，以人教版课本为例，在四年级下册的“数学广角”中，给了学生不同的解题方法，例如，列表法、抬脚法等。让我们由浅入深，去看看要解决此类问题有多少种方法。

一、画图法

低年级学生的逻辑思维还不是很强，通常会画图表达题目中的内容。

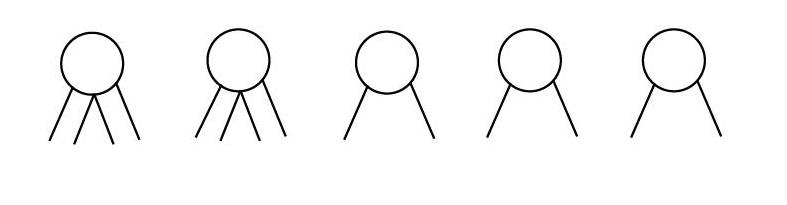
[例1]今有鸡和兔同笼，头5个，脚14只，笼中有鸡、兔各几只？

此时我们画图来表达，因为不清楚两种动物的数量，所以我们画图不做区分，都用小圆圈表示小动物的头和身，再添上脚，鸡有两只脚，兔子有四只脚，那么我们都画上两只脚，这样不足的再去补全，直到数出14只脚为止。如下图：

这种方法十分适合三年级以下的学生。在刚刚接触实际问题时，难免会在读题上出现问题，觉得文字题难理解，无法转化成学过的知识。画图法则直观地呈现出了题目中的信息，既可以帮助学生理解题意，又能提升学生的兴趣，使学生发现解决实际问题的乐趣。

二、列表法

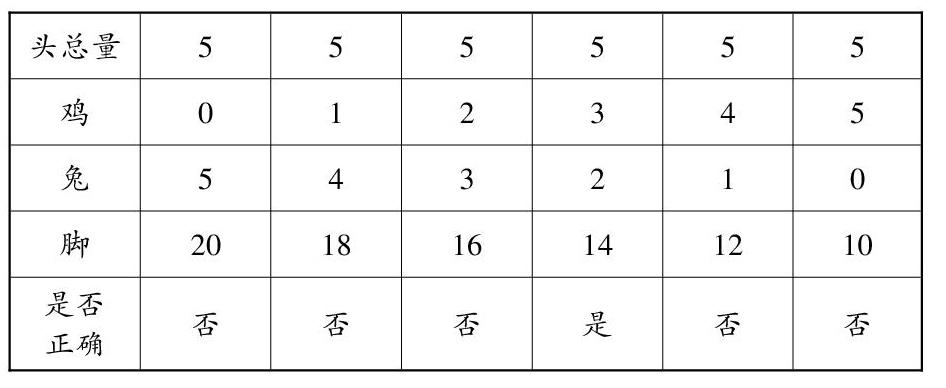
在学生学习更多运算后，数字这一概念会被重视，站在数字的角度来思考时，学生就可以利用列表法来解题，以例1题目为例，可从鸡的数量为0开始列表，直到满足脚的数量为14只。分析后可列出下表：

这种方法对低年级学生依然适用，这种方法虽然稍显麻烦，但是非常有逻辑性，可以适当引导学生使用列表法，但不要生搬硬套，这样才能及时找到正确答案。另外，数据较大时，教师可以引导学生根据数据的特点，按一定的间隔或从中间数开始列举，不断优化列举法，灵活快捷地解决问题。

三、假设法

小学的学习是帮助学生建立数学思维的过程，在不断的探索中，学生会把解决问题的整体思路偏向于抽象思维，而不再沉浸于表面。中年级学生学了四则运算，就可以利用假设法去思考并列式来解决问题。假设法是根据题目中的已知条件或结论做出某种假设，将复杂的问题简单化，从而迅速找到解题思路。

[例2]有鸡和兔同笼，头19个，脚58只，笼中有鸡、兔各几只？

①假设笼中全部是鸡

假设笼中全部是鸡，那么脚有38只，还剩余20只脚，我们需要把现有的鸡换成兔，将剩余的脚的数量换成兔，1只兔换1只鸡，就需要补2只脚，换了几次就是兔的数量。分析后可列式求兔的数量：（58-19x2）÷（4-2），算得兔有10只，鸡有19-10=9（只）。同理可假设笼中全部为兔，列式求鸡的数量：（19x4-58）÷（4-2）。

②假设抬脚

假设笼中的动物都抬起2只脚，此时笼中动物有38只脚抬起，而鸡的脚有2只，说明剩余的脚的数量都是兔的脚，每只兔只剩2只脚，此时我们将剩余的每两只脚确定一只兔，就可确定兔的数量。分析后可列式求兔的数量：（58-19x2）÷（4-2），算得兔有10只，鸡有19-10=9（只）。

相对于上面的假设笼中全部是鸡的算式是一样的，思路虽然有不同，但整体非常相似，个人认为，假设抬脚这种方法趣味性更高，更能帮助学生理解问题。

假设法是解决问题的一种蹊径，更是数学教学的难点，在运用上不光要理解假设法，还需要根据假设法列出正确式子，帮助学生提升数学思维。

四、方程法

高年级的学生认知能力逐渐升级，从抽象思维慢慢转化成逻辑推理，这时他们开始接触方程。在列方程的过程中，要让学生结合实际问题，利用已知条件去找等量关系，然后列出式子。以例2为例题，来总结方程的用法。此时我们可以设鸡的数量为x只，那么由“头的数量19个”可知兔有（19-x）只，再读到下句话中得知脚有58只，鸡有2x只脚，兔有4（19-x）只脚，可用脚的总数量列出方程：2x+4（19-x）=58。

方程法是后期学生解决实际问题时的一个常用方法，在分数除法、行程问题中都应用广泛。小学阶段的方程延伸到初中，会演变出二元一次方程组，与鸡兔同笼同理，是根据两个量的不同关系来列出两个不同方程，结合在一起后找到方程的解从而解决问题。方程法的实用性由此可见。

通过上述不同阶段的学生对于解决“鸡兔同笼”问题方法的分析，我做出以下总结：低年级学生的数学思维还没有完全形成，更关注表象，所以学生解题采用画图法来解题;中年级学生在学习过程中逐渐认识到了数字的重要性，在不断用数量关系解题的过程中，更是不断提升自己的逻辑性，所以学生解题会有一些尝试性的方法体现出来，在优化方法的过程中，学生的数学思维更加抽象化，逻辑性增强，此时学生的思路不再常规化，而更加多样化;高年级学生的数学思维逐渐转化为逻辑推理，并能把方法优化成省时省力且正确率高的方法，不断运用最优方法解决问题。

“鸡兔同笼”问题有多种变形，例如一家人出行买票问题，分段行程问题。学生在不斷的应用中不仅能锻炼思维，更能体会到数学的趣味性和多样性。针对不同阶段的学生，教师要有针对性地备课和讲解，有效地帮助学生理解不同的解题方法，以达到良好的教学效果。

（责编：黄露）