AZ31镁合金位错密度模型及热压缩的微观组织预测

汪建强，郭丽丽，王长峰

AZ31镁合金位错密度模型及热压缩的微观组织预测

汪建强，郭丽丽，王长峰

(大连交通大学 材料科学与工程学院 连续挤压教育部工程研究中心，大连 116028)

通过热压缩实验研究AZ31镁合金挤压杆料在变形温度300、400和500 ℃，应变速率0.1、0.01和0.001 s−1条件下的流变行为，基于Arrhenius方程建立流变应力的本构模型，其中激活能为132.45 kJ/mol，应变硬化系数为4.67。依据AZ31镁合金高温变形中的动态再结晶(Dynamic recrystallization，DRX)机理和位错密度演化规律，建立宏观变形−微观组织多尺度耦合的位错密度模型，该模型能够反映热加工过程中的加工硬化、动态回复(Dynamic recovery，DRV)、低角晶界(Low angle grain boundaries，LAGB)和高角晶界(High angle grain boundaries，HAGB)等机制的交互作用。利用ABAQUS的VUSDFLD子程序进行热压缩过程的有限元模拟，获得DRX分数、LAGB和HAGB位错密度的数值模拟结果以及压缩载荷。结果表明：实验载荷与模拟结果基本吻合，本文提出的AZ31镁合金位错密度模型是合理的。

AZ31镁合金；本构模型；位错密度模型；有限元模拟

镁及镁合金是最轻的结构材料，具有密度小、比强度高和良好的可焊性等优点，被广泛地应用于电子、汽车和航空产业[1−2]。但由于其为密排六方结构，常温下能开动的滑移系较少，塑性成形性差[3−5]，然而，非基面滑移系的临界剪切应力随着温度的升高而降低，致使其微观组织演化机理随加工条件而变化[6−7]。因此，应用合适的数学模型对镁合金中高温变形过程中的微观组织进行预测，对把握镁合金变形规律、揭示微观机理有重要意义。

镁合金中高温变形及其DRX行为的相关研究很多，在不同变形条件下镁合金的DRX程度不同，控制其再结晶的微观机制亦不相同。镁合金根据变形温度一般可将DRX分为低温(200 ℃以下)的孪晶动态再结晶(Twin DRX, TDRX)，中温(200~250 ℃)的TDRX和连续动态再结晶(Continuous DRX, CDRX)和高温(250 ℃以上)的CDRX和不连续动态再结晶(Discontinuous DRX, DDRX)[8−10]。ION等[11]通过分析150~330 ℃下镁合金压缩试验后的微观组织，发现随着变形量的增加LAGB逐渐转变为HAGB，并将这种再结晶模式命名为旋转动态再结晶(Rotational DRX, RDRX)。由于这种再结晶过程中并没有明显的形核和长大现象，HUMPHREYS等[12]和LI等[13]把这种再结晶机制归为CDRX。SITDIKOV等[9]认为纯镁在高温区会出晶界弓出的DDRX，但在再结晶过程中DDRX所占比例很小，主要是CDRX。镁合金在基面的层错能较低，但在中高温下，交滑移导致原始晶界附近的位错滑移面转化为非基面，此时的层错能至少是原来的4倍[8]，因此，在高层错能材料中发生的CDRX在镁合金的中高温变形中起主导作用。CDRX机制是应变硬化产生的位错经过滑移在晶界处出现塞积形成亚晶界，亚晶界不断的吸收位错，晶界角由低角向高角转变，形成再结晶晶粒，HAGB继续吸收位错，通过迁移使晶粒长大的过程[14]。

目前，应用较多的微观组织模型是根据金属在压缩或拉伸变形过程中的流变应力曲线和再结晶的经典理论建立，即为基于流变应力的微观组织本构模型，此类模型在钢铁、铝合金材料的微观组织预测上应用较多，但是由于只考虑流变应力的变化情况，缺乏必要的材料微观组织演化过程的支撑[15−17]。金属塑性变形的主要方式是滑移和孪生，滑移的本质是位错的运动，通过位错的协调满足应变的需求，塑性变形能存储在位错中，为DRX和DRV提供驱动力，因此，位错密度是材料内部微观组织变化的关键变量。经典又具有代表性的位错密度模型有E−M模型[18](式(1))和K−M模型[12](式(2))。

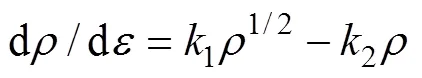
式中：为加工硬化参数；为回复软化参数；为位错密度；1和2为材料常数。

GOURDET等[19]建立了纯铝基于位错密度的CDRX本构模型，通过应变硬化、DRV和HAGB的迁移来解释CDRX位错密度变化；PARVIN等[20]提出了在大塑性变形下考虑堆垛层错能的位错密度模型；DINI等[21]将AZ91镁合金的位错密度演变模型分为应变硬化使位错密度增加和DRV使位错密度湮灭。上述模型都是以位错密度为中间变量，位错密度与应变之间是确定的函数关系，但以上模型中都缺少时间变量，均无法预测微观组织随加工时间的变化情况，难以反映镁合金在加工过程中的CDRX机理。GUO等[22]研究了AZ31镁合金在热轧过程中的微观组织演化，采用CDRX机制建立了含有时间变量的位错密度简化模型，但该模型并未考虑热加工中应变速率和DRX体积分数对位错密度的影响。

本文通过热压缩实验，建立了AZ31镁合金高温流变应力的本构模型，依据镁合金高温变形中的DRX机制和位错演化规律，考虑了应变速率、DRX体积分数、温度和时间变量对位错密度的影响，最终建立了宏观变形−微观组织(位错密度)多尺度耦合模型。利用ABAQUS软件中的VUSDFLD子程序嵌入建立的位错密度模型进行热压缩过程的有限元模拟，并通过实验载荷和模拟结果的压缩反力对比，为镁合金的塑性变形研究提供理论依据。

1 热压缩实验及流变应力本构模型

1.1 热压缩实验

实验所用的材料为AZ31镁合金挤压杆料，试样尺寸为8 mm×12 mm圆柱体，在AG-100KN电子万能高温材料试验机上进行热压缩实验，采用Raytek红外测温仪测量实验过程中试样温度的变化。实验的变形温度为300、400和500 ℃，变形速率为0.1、0.01和0.001 s−1。实验结束时对试样及时水淬处理，以保留材料压缩变形后的微观组织，变形前后压缩试样如图1所示。通过实验获得了真实应力−应变曲线，如图2所示。

图1 AZ31镁合金压缩试样

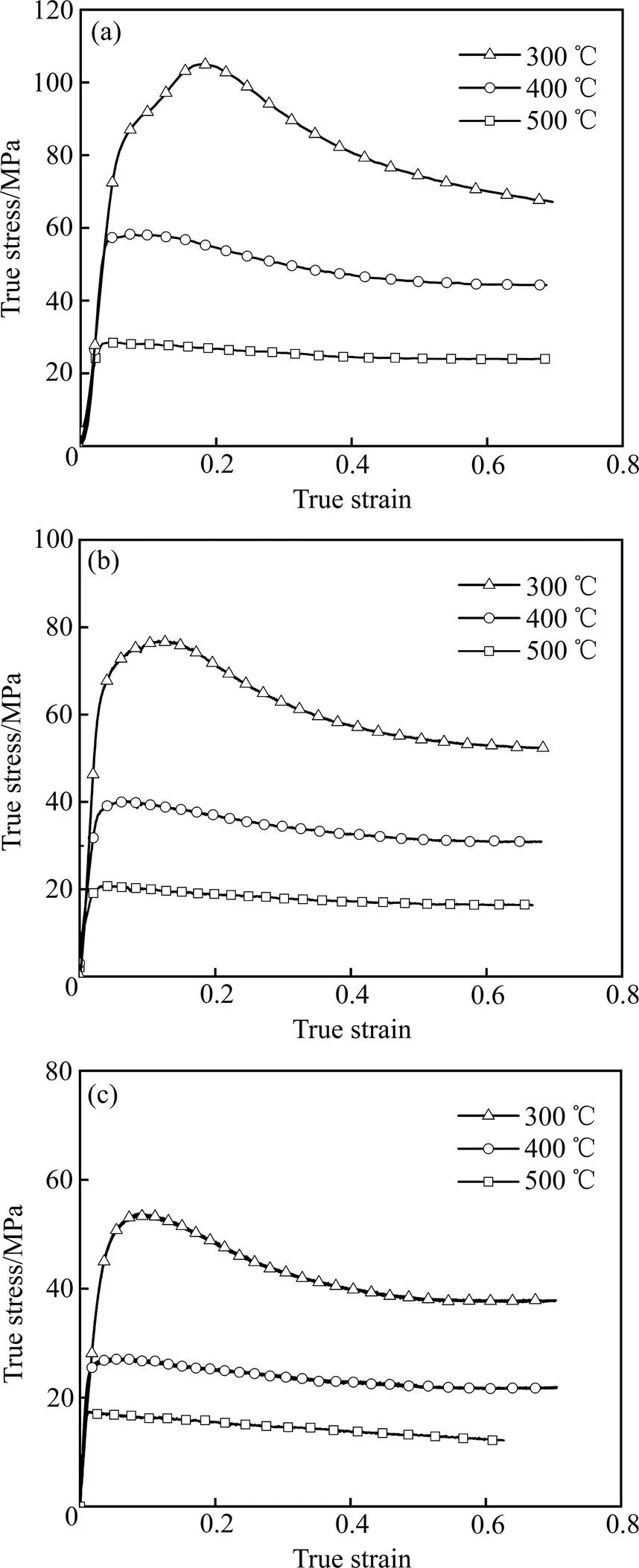
图2 AZ31镁合金的真实应力−真实应变曲线

1.2 流变应力本构模型

SELLARS[23]指出热加工的塑性变形与高温蠕变发生在相似的温度范围，具有类似的热激活机制。因此，可以认为稳态应力取决于温度和应变速率，并使用蠕变方程进行建模如下：

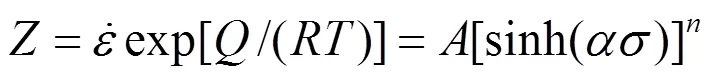
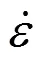
由于该模型中并没有体现出应变因素的影响，因此只能表示稳态应力。为了能够更好地描述热加工过程，一些学者[24−26]在E−M模型的基础上采用了分段函数的形式来构建模型，分为伴随有DRV的加工硬化阶段和DRX的软化阶段。DRX体积分数DRX是DRX中关键变量，LIU等[27]基于Sellars模型、Kopp模型和Yada模型提出了新的DRX体积分数模型(式(4))，结果表明其预测值与实验很好的吻合，有效地揭示了AZ31镁合金热成形过程DRX演变规律。

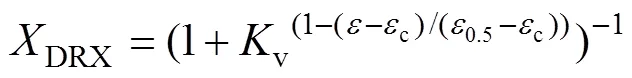
1.3 模型参数的确定

在热加工中，低应力水平下流变应力与应变速率之间的关系用指数关系描述：

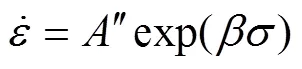
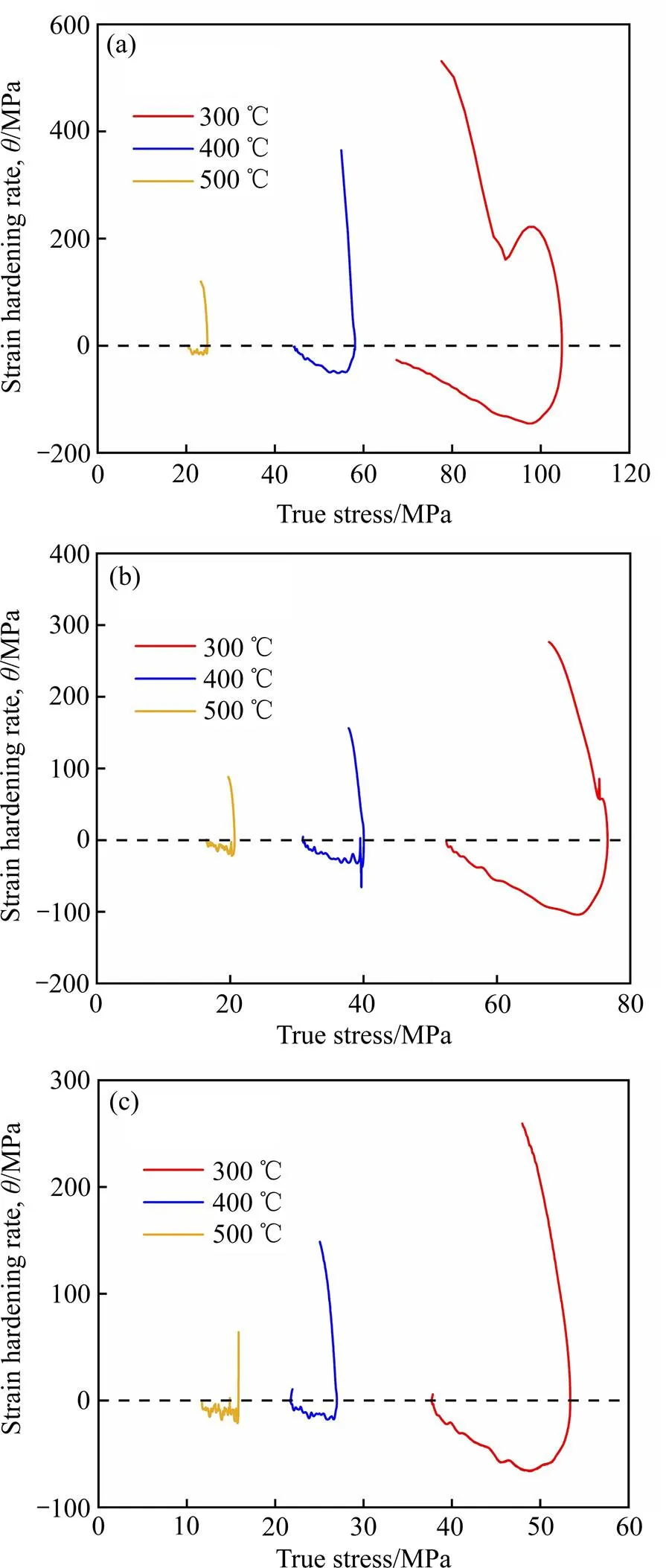
图3 应变硬化率θ−真实应力曲线

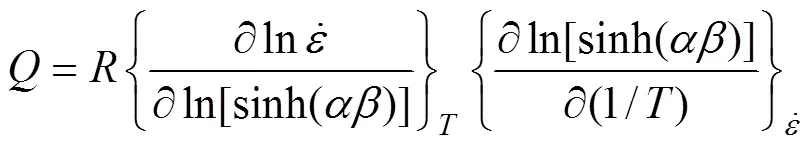
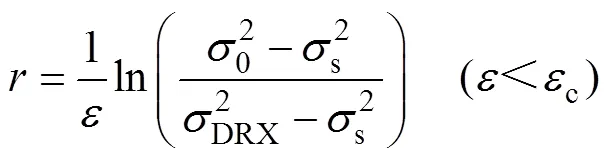
图4 峰值应力与应变速率和温度的线性关系

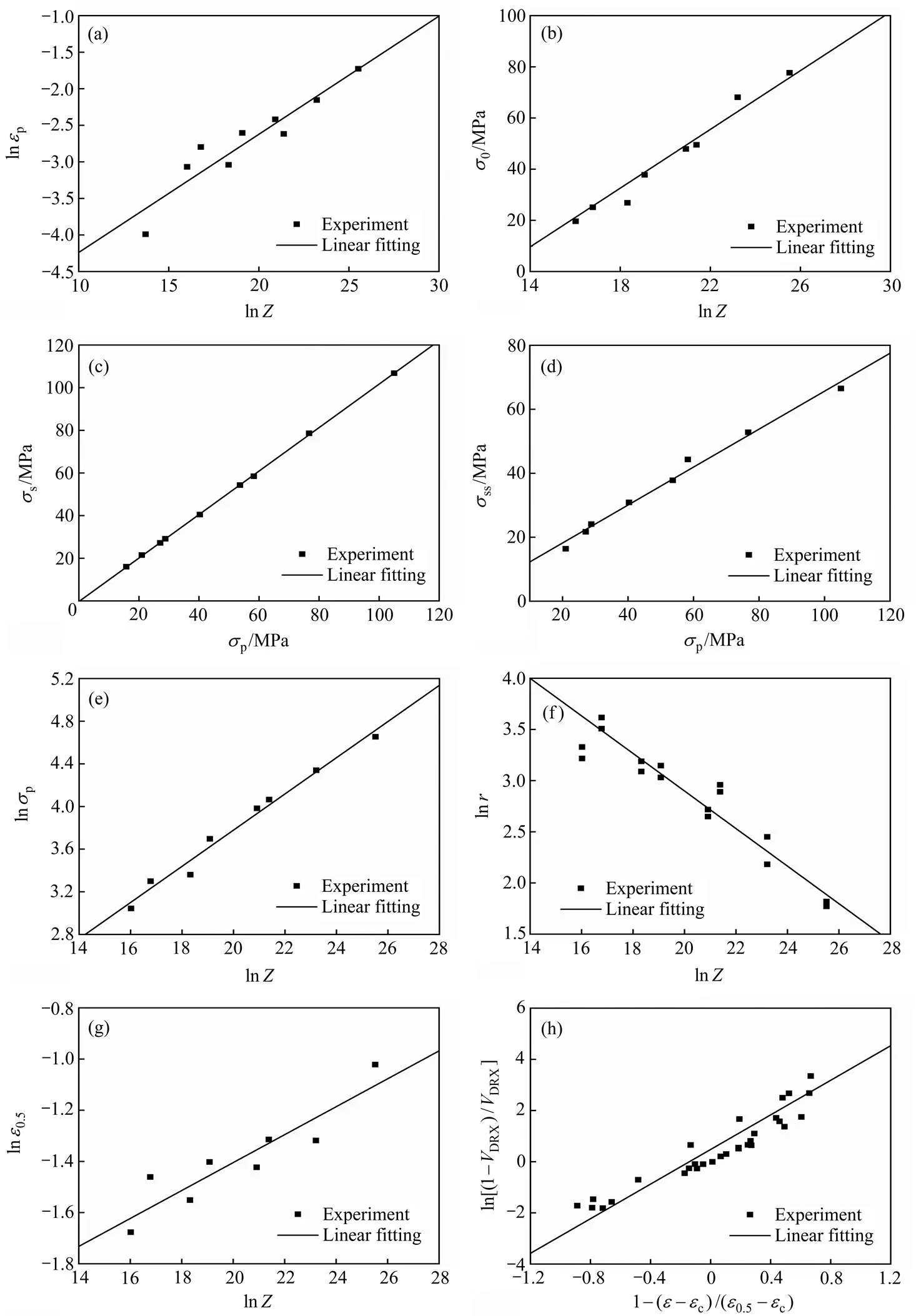
图5 线性拟合曲线

1.4 模型精度评价

运用建立的流变应力本构模型(式(10))预测AZ31镁合金真实应力−应变曲线，并与实验结果对比可知二者基本吻合，如图6所示。进而评价了模型的精度，采用相关系数cc和平均相对误差Re(Mean relative error)对模型的预测值进行统计学误差评价。

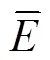
2 位错密度模型

镁合金CDRX产生的位错密度转化过程可分为以下5个部分，如图7所示。

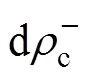
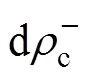
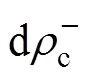
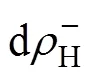
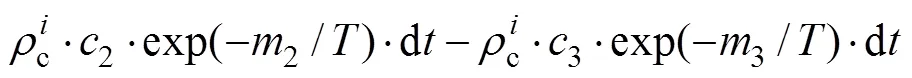
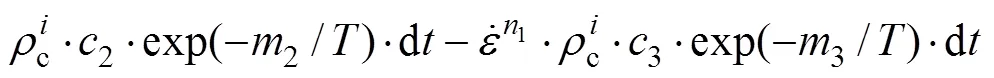
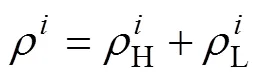
(20)

3 高温压缩有限元数值模拟

ABAQUS软件为用户提供了强大而又灵活的用户子程序接口(User subroutine)和应用程序接口(Utility routine)。本文采用ABAQUS中的VUSDFLD子程序接口，运用Fortran语言对新建立的位错密度模型编写接口程序，使用VGETVRM方法方便地获取材料点参数，重新定义材料点的场变量，使之作为时间的函数。将DRX体积分数、HAGB和LAGB位错密度等定义为解依赖的状态变量，在数值模拟结果中可以显示相对应的云图。图8所示为Fortran语言编写VUSDFLD子程序接口的程序流程图。

图8 Fortran语言编写VUSDFLD子程序接口的程序流程图

利用上述建立的AZ31镁合金的微观组织模型(见式(15)~(20))和AZ31镁合金材料属性(见表1[33−35])进行热压缩过程的有限元数值模拟，模拟结果的压缩载荷随时间的变化曲线与实验获得曲线进行比较可知，二者趋势一致，吻合度较高，如图9所示。图中给出了当应变速率0.01 s−1温度400 ℃时，利用式(13)和(14)的未修正位错密度模型预测的结果，发现修正后的位错密度模型较真实地反映了宏观的AZ31镁合金热压缩过程中的应变硬化、DRV和DRX软化导致的载荷变化情况。根据实验和模拟结果确定了位错密度模型中各参数值，如表2所列。

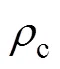
表1 AZ31镁合金材料属性[33−35]

表2 AZ31镁合金位错密度模型参数

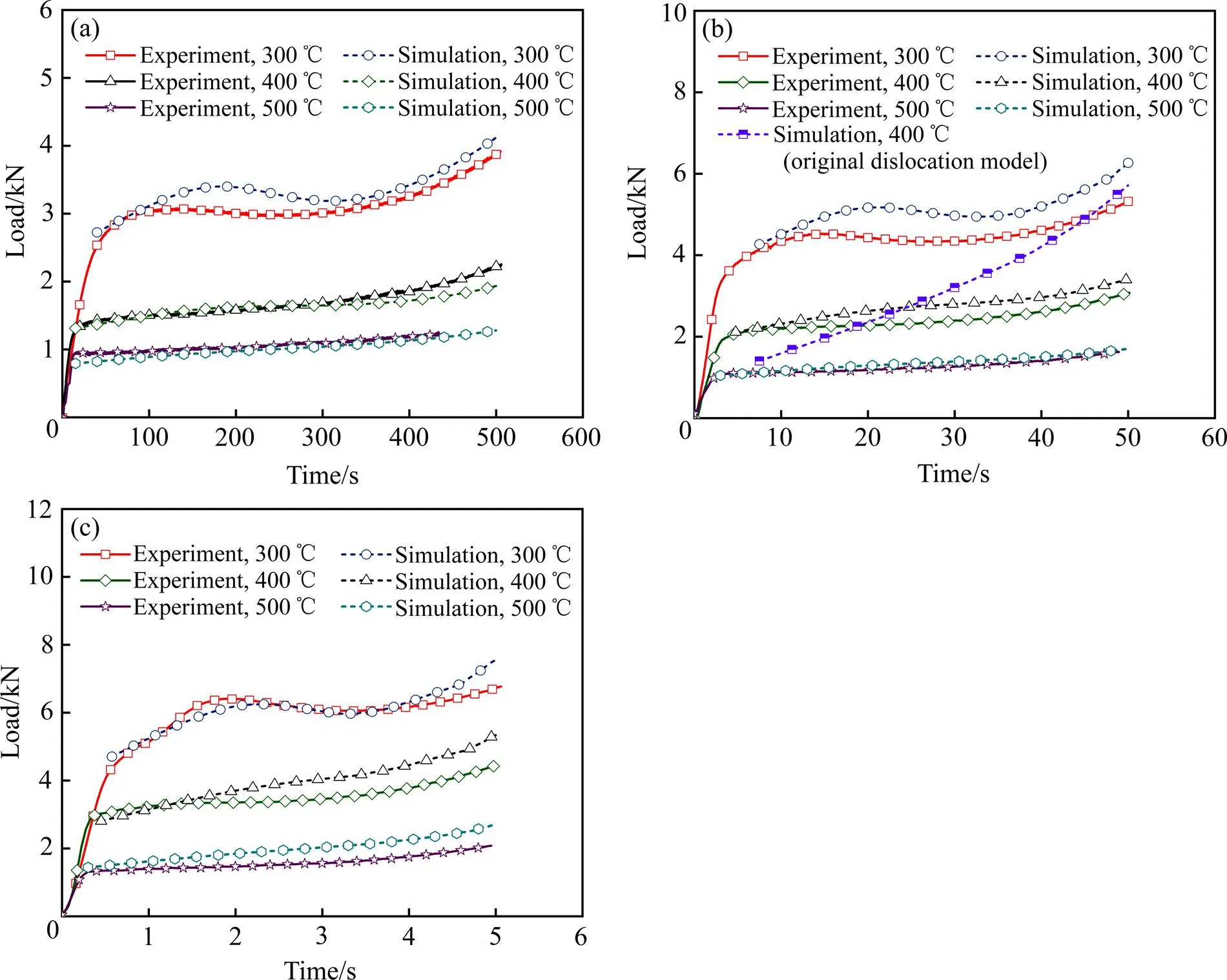
图9 实验和模拟结果的载荷随时间的变化曲线

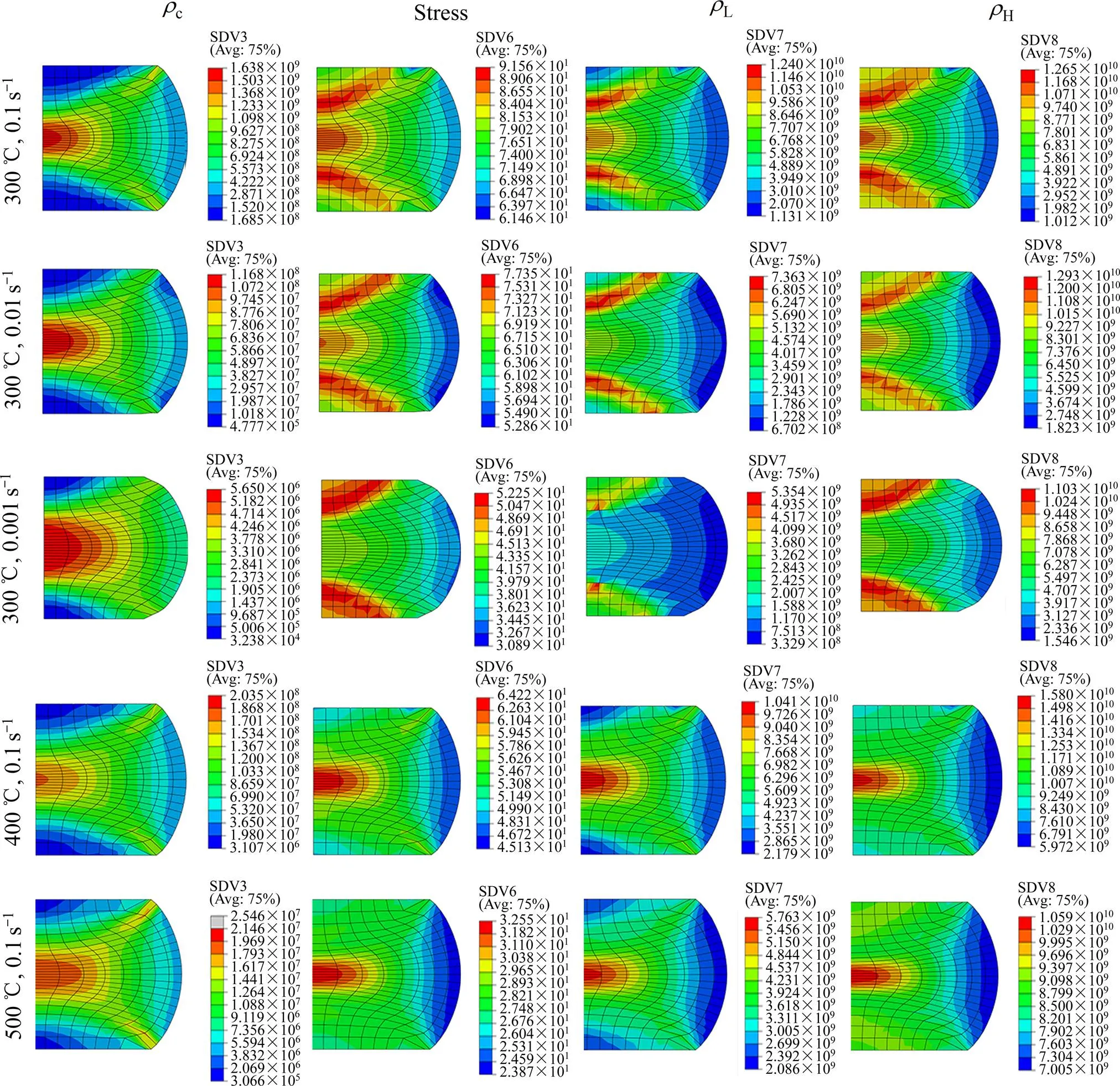
图10 晶胞内自由位错密度、应力、LAGB位错密度和HAGB位错密度云图

GOURDET等[19]提出了铝合金的CDRX位错密度模型，计算了晶胞内自由位错密度，并得出LAGB位错密度随应变速率的升高而升高，随温度的升高而降低的规律。GUO等[36]通过EBSD实验研究了不同轧制参数对AZ31镁合金DRX微观组织演化的影响，结果表明：LAGB%随着温度的升高而降低，HAGB%随着温度的升高出现增长停滞或下降趋势。VALIEV 等[37]研究表明应变速率对镁合金位错密度的影响显著，位错密度随着应变速率的增加而增加。上述的研究结果与本文建立的位错密度模型预测的LAGB和HAGB位错密度的结果有相同趋势，由此验证了所建模型的合理性。

4 结论

1) 通过热压缩实验，构建了基于Arrhenius方程的AZ31镁合金流变应力的本构模型，其中激活能为132.45 kJ/mol，应变硬化系数为4.67。校核了模型的精度，模型预测值与实验值的相关系数cc为0.99693，平均相对误差Re为5.06%。

2) 依据AZ31镁合金高温变形中的DRX机理，提出了新的含有时间变量的位错密度模型。通过热压缩过程的微观组织模拟，获得了压缩载荷和时间的关系曲线，与实验结果吻合较好，由此确定了位错密度模型中的参数值。

[1] GUO L, FUJITA F. Influence of rolling parameters on dynamically recrystallized microstructures in AZ31 magnesium alloy sheets[J]. Journal of Magnesium and Alloys, 2015, 3(2): 95−105.

[2] MORDIKE B L, EBERT T. Magnesium: Properties- applications-potential[J]. Materials Science and Engineering A, 2001, 302(1): 37−45.

[3] KIM H L, LEE J H, LEE C S, BANG W, AHN S H, CHANG Y W. Shear band formation during hot compression of AZ31 Mg alloy sheets[J]. Materials Science and Engineering A, 2012, 558: 431−438.

[4] JIA W P, HU X D, ZHAO H Y, JU D Y, CHEN D L. Texture evolution of AZ31 magnesium alloy sheets during warm rolling[J]. Journal of Alloys and Compounds, 2015, 645: 70−77.

[5] 郭丽丽, 符 蓉, 裴久杨, 杨俊英, 宋宝韫. AZ31 镁合金板材连续挤压工艺的实验研究[J]. 稀有金属材料与工程, 2017, 46(6): 1626−1631. GUO Li-li, FU Rong, PEI Jiu-yang,YANG Jun-ying, SONG Bao-yunExperimental studies on AZ31 magnesium sheets processed by continuous extrusion[J]. Rare Metal Materials and Engineering, 2017, 46(6): 1626−1631.

[6] ROODPOSHTI P S, SARKAR A, MURTY K L. Microstructural development of high temperature deformed AZ31 magnesium alloys[J]. Materials Science and Engineering A, 2015, 626: 195−202.

[7] STEINER M A, BHATTACHARYYA J J, AGNEW S R. The origin and enhancement of {0001} <112-10> texture during heat treatment of rolled AZ31B magnesium alloys[J]. Acta Materialia, 2015, 95: 443−455.

[8] GALIYEV A, KAIBYSHEV R, GOTTSTEIN G. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60[J]. Acta Materialia, 2001, 49(7): 1199−1207.

[9] SITDIKOV O, KAIBYSHEV R. Dynamic recrystallization in pure magnesium[J]. Materials Transactions, 2001, 42(9): 1928−1937.

[10] 刘楚明, 刘子娟, 朱秀荣, 周海涛. 镁及镁合金动态再结晶研究进展[J]. 中国有色金属学报, 2006, 16(1): 1−12. LIU Chu-ming, LIU Zi-juan, ZHU Xiu-rong, ZHOU Hai-tao. Research and development progress of dynamic recrystallization in pure magnesium and its alloys[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(1): 1−12.

[11] ION S E, HUMPHREYS F J, WHITE S H. Dynamic recrystallisation and the development of microstructure during the high temperature deformation of magnesium[J]. Acta Metallurgica, 1982, 30(10): 1909−1919.

[12] HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena[M]. Oxford: Elsevier, 2004: 1−574.

[13] LI S B, WANG Y Q, ZHENG M Y, WU K. Dynamic recrystallization of AZ91 magnesium alloy during compression deformation at elevated temperature[J]. Transactions of Nonferrous Metals Society of China, 2004, 14(2): 306−310.

[14] HUANG K, LOGÉ R E. A review of dynamic recrystallization phenomena in metallic materials[J]. Materials & Design, 2016, 111: 548−574.

[15] CHEN M S, LIN Y C, LI K K, ZHOU Y. A new method to establish dynamic recrystallization kinetics model of a typical solution-treated Ni-based superalloy[J]. Computational Materials Science, 2016, 122: 150−158.

[16] ZHAO D, YANG Y, ZHOU J, LIU YU, TANG S. Constitutive modeling for dynamic recrystallization kinetics of Mg-4Zn-2Al-2Sn alloy[J]. Transactions of Nonferrous Metals Society of China, 2018, 28(2): 340−347.

[17] YI Y, FU X, CUI J, CHEN H. Prediction of grain size for large-sized aluminium alloy 7050 forging during hot forming[J]. Journal of Central South University of Technology, 2008, 15(1): 1−5.

[18] ESTRIN Y, MECKING H. A unified phenomenological description of work hardening and creep based on one-parameter models[J]. Acta Metallurgica, 1984, 32(1): 57−70.

[19] GOURDET S, MONTHEILLET F. A model of continuous dynamic recrystallization[J]. Acta Materialia, 2003, 51(9): 2685−2699.

[20] PARVIN H, KAZEMINEZHAD M. Development a dislocation density based model considering the effect of stacking fault energy: Severe plastic deformation[J]. Computational Materials Science, 2014, 95: 250−255.

[21] DINI H, SVOBODA A, ANDERSSON N E, GHASSEMALI E, LINDGREN L E, JARFORS A E. Optimization and validation of a dislocation density based constitutive model for as-cast Mg-9%Al-1%Zn[J]. Materials Science and Engineering A, 2018, 710: 17−26.

[22] GUO L, FUJITA F. Modeling the microstructure evolution in AZ31 magnesium alloys during hot rolling[J]. Journal of Materials Processing Technology, 2018, 255: 716−723.

[23] SELLARS C M. Modelling microstructural development during hot rolling[J]. Materials Science and technology, 1990, 6(11): 1072−1081.

[24] LIU J, CUI Z, LI C. Modelling of flow stress characterizing dynamic recrystallization for magnesium alloy AZ31B[J]. Computational Materials Science, 2008, 41(3): 375−382.

[25] ZHAO D, YANG Y, ZHOU J, YU L, TANG S. Constitutive modeling for dynamic recrystallization kinetics of Mg-4Zn-2Al-2Sn alloy[J]. Transactions of Nonferrous Metals Society of China, 2018, 28(2): 340−347.

[26] 胡丽娟. AZ31镁合金板材温热变形行为的数值分析与试验研究[D]. 上海: 上海交通大学, 2009: 1−122. HU Li-juan. AZ31 numerical and experimental studies on warm deforming of az31 magnesium alloy sheet[D]. Shanghai: Shanghai Jiao Tong University, 2009: 1−111.

[27] LIU J, CUI Z, RUAN L. A new kinetics model of dynamic recrystallization for magnesium alloy AZ31B[J]. Materials Science and Engineering A, 2011, 529: 300−310.

[28] NAJAFIZADEH A, JONAS J J. Predicting the critical stress for initiation of dynamic recrystallization[J]. ISIJ International, 2006, 46(11): 1679−1684.

[29] DING H, HIRAI K, HOMMA T, KAMADO S. Numerical simulation for microstructure evolution in AM50 Mg alloy during hot rolling[J]. Computational Materials Science, 2010, 47(4): 919−925.

[30] 胡丽娟, 彭颖红, 唐伟琴, 李大永, 张少睿. AZ31 镁合金薄板动态再结晶对其拉伸性能的影响[J]. 中国有色金属学报, 2008, 18(9): 1571−1576. HU Li-juan, PENG Ying-hong, TANG Wei-qin, LI Da-yong, ZHANG Shao-rui. Effect of dynamic recrystallization on tensile properties of AZ31 magnesium alloy sheet[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(9): 1571−1576.

[31] 刘 娟, 李居强, 崔振山, 阮立群. 新的单参数动态再结晶动力学建模及晶粒尺寸预测[J]. 金属学报, 2012, 48(12): 1510−1519. LIU Juan, LI Ju-qiang, CUI Zhen-shan, RUAN Li-qun. A new one-parameter kinetics model of dynamic recrystallization and grain size predication[J]. Acta Metallurgica Sinica, 2012, 48(12): 1510−1519.

[32] 孙 宇, 周 琛, 万志鹏, 任丽丽, 胡连喜. 金属材料动态再结晶模型研究现状[J]. 材料导报, 2017(13): 12−16. SUN Yu, ZHOU Chen, WAN Zhi-peng, REN Li-li, HU Lian-xi. Current research status of dynamic recrystallization model of metallic materials[J]. Materials Review, 2017(13): 12−16.

[33] JUAN H L, PENG Y H, YONG L D, RUI Z S. Influence of dynamic recrystallization on tensile properties of AZ31B magnesium alloy sheet[J]. Materials and Manufacturing Processes, 2010, 25(8): 880−887.

[34] JIN Z, YIN K, YAN K, WU D, LIU J, CUI Z. Finite element modelling on microstructure evolution during multi-pass hot compression for AZ31 alloys using incremental method[J]. Journal of materials science & technology, 2017, 33(11): 1255−1262.

[35] 郭丽丽, 王长峰, 詹 鉴. 基于二次开发的 AZ31 镁合金热轧有限元模拟和实验研究[J]. 塑性工程学报, 2017, 24(6): 48−54. GUO Li-li, WANG Chang-feng, ZHAN Jian. Experimental studies and finite element simulation on AZ31 magnesium alloy during hot rolling based on secondary development[J]. Journal of Plasticity Engineering, 2017, 24(6): 48−54.

[36] GUO L, FUJITA F. Influence of rolling parameters on dynamically recrystallized microstructures in AZ31 magnesium alloy sheets[J]. Journal of Magnesium and Alloys, 2015, 3(2): 95−105.

[37] VALIEV R Z, KAIBYSHEV O A. Mechanism of superplastic deformation in a magnesium alloy. Ⅱ. The role of grain boundaries[J]. Physica Status Solidi (A), 1977, 44(2): 477−484.

Dislocation density model of AZ31 magnesium alloy and microstructure prediction of thermal compression

WANG Jian-qiang, GUO Li-li, WANG Chang-feng

(Continuous Extrusion Engineering Research Center, Ministry of Education, School of Materials Science and Engineering, Dalian Jiaotong University, Dalian 116028)

Thermal-mechanical behavior of AZ31 magnesium alloy extruded rod was investigated by thermal compression experiment at the deformation temperatures of 300, 400, 500 ℃ and the strain rates of 0.1, 0.01, 0.001 s−1. A flow stress constitutive model of the alloy was established based on the regression analysis by the Arrhenius type equation. The activation energyis 132.45 kJ/mol and the strain hardening coefficientis 4.67. According to the dynamic recrystallization (DRX) mechanism of AZ31 magnesium alloy at high temperature deformation, a multi-scale coupled dislocation density model of macroscopic deformation-microstructure of magnesium alloy during high temperature deformation was proposed. The model could reflect the interactions among work hardening, dynamic recovery (DRV), transformation from low angle grain boundaries (LAGB) into high angle grain boundaries (HAGB) and mechanisms during the hot working process. Furthermore, the finite element simulation of the compression process was performed by VUSDFLD subroutines in ABAQUS software. As a result, DRX volume fraction, compression force, and the dislocation density of HAGB and LAGB are obtained. It is obvious that the simulated results are similar to the experimental force. The new proposed dislocation density model of AZ31 magnesium alloy is reasonable.

AZ31 magnesium alloy; constitutive model; dislocation density model; finite element simulation

Project(51401043) supported by the Youth Program of National Natural Science Foundation of China

2018-12-07;

2019-06-24

GUO Li-li; Tel: +86-411-84106527; E-mail: guolili0822@hotmail.com

1004-0609(2020)-01-0048-12

TG146.2+2

A

10.11817/j.ysxb.1004.0609.2020-37477

国家自然科学基金青年基金资助项目(51401043)

2018-12-07；

2019-06-24

郭丽丽，副教授，博士；电话：0411-84106527；E-mail：guolili0822@hotmail.com

(编辑 王 超)