微量液体高精度加样的数值仿真研究

2020-04-01闫慧敏和发展刘耀基

中国医学装备 2020年3期

闫慧敏杨伟和发展刘耀基王超*

近年来，随着国民健康意识的增强，各大医院、检验中心生化检测数量快速上升，同时许多疾病的精准诊断越来越依赖于高精度的生化定量分析，促使了全自动化学发光分析仪朝着高速高精度方向发展[1]。加样速度与精度是影响高速高精度检测的关键因素之一[2]。目前，试剂的加样量都在微升量级，加样精度的控制直接影响到检测结果的准确性，加样方式中多采用空气柱隔离的方式，将系统液和试剂进行隔离，避免了试剂在针内被系统液稀释的风险。为了确保仪器的加样系统能够精确地定量试剂，掌握加样针内的试剂的运动状态和加样状态至关重要。因此，本研究采用流体仿真软件，以纯化水为研究介质，采用流体仿真的方法复现实际加样的过程，并结合理论分析和实验结果，分析加样速度与加样量等因素对加样过程的动态特性的影响，为微量液体高精度加样提供理论支持。

1 材料与方法

1.1 研究材料

加样针属于加样系统重要部件之一[3-4]。采用市场上一款加样针，针内壁直径从针尾到针尖由1.2 mm过渡到0.5 mm，针尖有斜角，材料为不锈钢，外壁有涂层，材料为特氟龙。反应杯的外观结构为T型，其材质为聚丙烯，物理和化学特性稳定，外观透明且易于观察。本研究给定加样针在反应杯中的位置，其在反应杯中的加样状态、加样针及其结构见图1。

1.2 流体运动

当圆管内黏滞力对流场的影响大于惯性力时，流体分层流动，相邻的流层之间存在相互滑动，仅在切线方向产生作用力，流体运动为层流；当惯性力对流场的影响大于黏滞力时，除了在切线方向产生作用力，在垂直切线方向存在压差和升力作用，这种运动称为湍流[5-7]。当雷诺数(Re)＜2000时，流体运动为层流，当4000＞Re＞2000时，由层流向湍流过渡，当Re＞4000时，流体运动为湍流。圆管层流和湍流见图2。

当圆管内的流体处于层流运动时，靠近壁面的流速小，远离壁面的流速大，圆管内的流速以抛物线的方式分布；当圆管内的流体处于湍流运动时，相邻流层混合在一起，流场中出现许多漩涡，且旋涡不规则的运动。

图1 加样针及其结构示意图

图2 圆管层流和湍流示意图

在加样系统中，为实现空气隔离系统液和试剂，针内的流体应以层流的方式运动。本研究加样针内试剂采用纯化水代替，温度在(25±2)℃。在流体力学中，惯性力与粘性力的比值用Re来表示，其计算为公式1：

式中v为流体的流速(m/s)，d为圆管直径(m)，ρ为密度(kg/m3)，μ为流体动力粘滞系数[kg/(m-s)]。

经过计算可知：在加样针内径1.2 mm处，当加样速度v＜1.5 m/s，即Re＜2000时，为层流；当3.0 m/s＞v＞1.5 m/s，即4000＞Re＞2000时，由层流向湍流过渡；当v＞3.0 m/s，即Re＞4000时，为湍流。因此，为了实现空气隔离系统液和试剂，针内流体的运动速度应＜1.5 m/s。

1.3 仿真方法

仿真是通过数值求解控制流体流动的微分方程，从而得到不可压缩流体在某一连续区域上的离散分布，进而近似模拟二维或三维模型中流体的运动状态[8]。在满足流体连续性、质量守恒和动量守恒[9]前提下，采用多相流(volume of fluid，VOF)模型和标准K-ε方程，对微量液体高精度加样的动态特性进行数值仿真分析。

2 结果与分析

2.1 加样针内流体的运动状态

2.1.1 仿真分析

以加样针为仿真分析对象，应用三维软件建立加样针三维几何模型。根据加样针在反应杯中的加样位置，对加样针和反应杯建立的三维模型进行简化。由于几何模型是对称结构，故用二维模型进行仿真分析。加样针二维及三维模型和网格划分见图3。

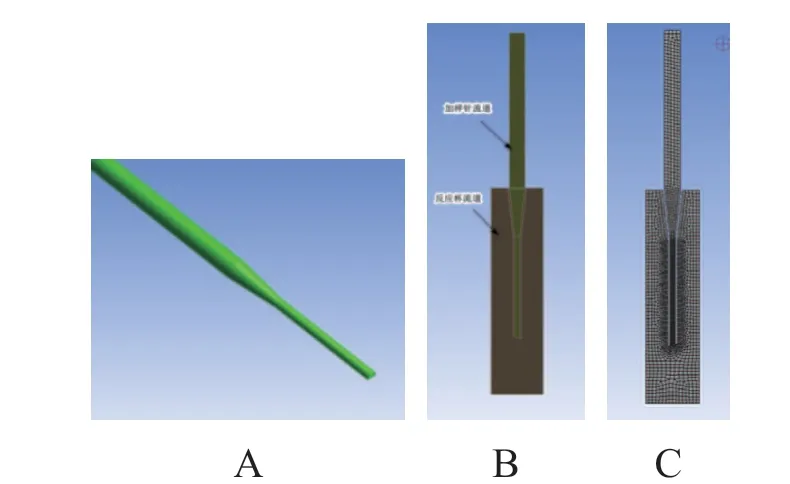
图3 加样针二维及三维模型和网格划分示意图

在满足流体连续性、质量守恒和动量守恒前提下，采用多相流VOF模型，两相介质分别是空气和纯化水，流动方程采用标准K-ε方程，针内壁设置一定的粗糙度，反应杯内壁设置为光滑壁面。运动状态边界条件见图4。

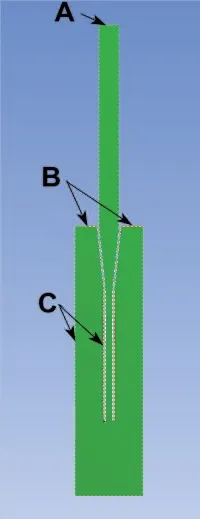
图4 运动状态边界条件示意图

(1)当步数(STEP)=0时，加样针和反应杯中空气体积占100%；STEP=1，入口两相体积中纯化水的体积设置为100%；STEP=2400时，入口两相体积中空气的体积设置为100%；STEP=3070时，入口两相体积中纯化水的体积设置为100%。模拟加样过程，纯化水和空气的流速均为0.1 m/s。加样针内流体运动随时间变化见图5。

由于加样针内壁具有一定的粗糙度，在加样针内径1.2 mm阶段，由于整体流速小，纯化水的动能不足以克服针内壁的摩擦力，纯化水沿着加样针内壁不规则流动，加样针内的空气和纯化水混合在一起，空气未能起到隔离的作用。

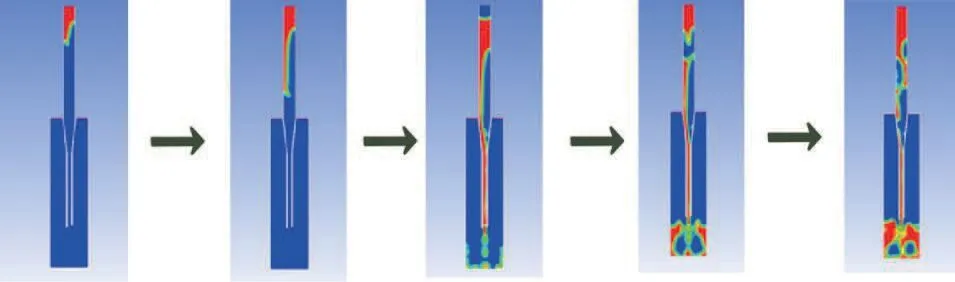
图5 流速为0.1 m/s时加样针内流体运动随时间变化示意图

(2)当STEP=0，加样针和反应杯中空气体积占100%；STEP=1，入口两相体积中纯化水的体积设置为100%；STEP=600时，入口两相体积中空气的体积设置为100%。模拟加样过程，纯化水和空气的速度均为1.2 m/s。

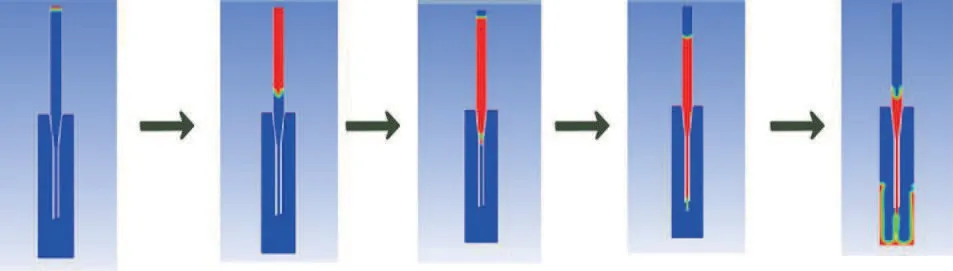
图6 流速为1.2 m/s时加样针内流体运动随时间变化示意图

加样针内壁具有一定的粗糙度，在加样针直径1.2 mm阶段，靠近加样针内壁的纯化水的速度相比远离加样针内壁的速度小，针内纯化水的流速以抛物线的方式分布，纯化水在加样针内的流动属于层流，仿真结果与理论分析一致。空气与纯化水有明确的边界，空气起到隔离的作用。加样针内纯化水流运动见图7。

图7 加样针内纯化水流运动示意图

通过仿真结果可知，在针内壁粗糙度不变的条件下，通过优化加样速度，液体的动态特性较稳定，空气柱能够起到隔离系统液与试剂的作用，有助于提高加样精度。

2.1.2 实验验证

搭建加样实验平台，在不同的加样速度条件下对加样系统进行定量测试。当加样速度在1.2 m/s条件下，注液量在99～101 μl范围内波动；加样速度在0.1 m/s条件下，注液量在97～102 μl范围内波动。因此，合理的优化加样速度，加样针的注液量波动范围较小，有助于提高加样的精度与稳定性，且实验结果与仿真结果一致。实验数据见图8。

2.2 加样针注液状态分析

根据仿真计算与实验验证，给定加样速度1.2 m/s，分析不同体积液体的加样状态。

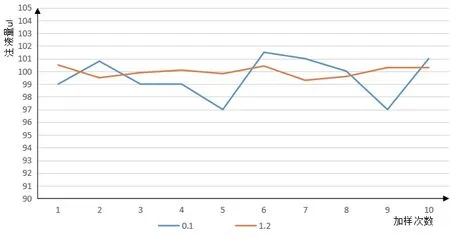
图8 实验数据

2.2.1 注液状态仿真

以反应杯作为主要仿真对象，对反应杯结构进行细化。为了减少提高仿真计算速度，优化加样针流道，仅将针尖部位作为研究对象。加样针二维模型和网格见图9。

图9 加样针和反应杯的二维模型和网格示意图

在满足流体连续性、质量守恒和动量守恒前提下，采用多相流VOF模型，两相介质分别是空气和纯化水，流动方程采用标准K-ε方程，反应杯内壁设置为光滑壁面。注液状态边界条件见图10。

图10 注液状态边界条件示意图

(1)当STEP=0，加样针和反应杯中空气体积占100%；STEP=1，入口两相体积中纯化水的体积设置为100%；STEP=1250时，入口两相体积中空气的体积设置为100%。

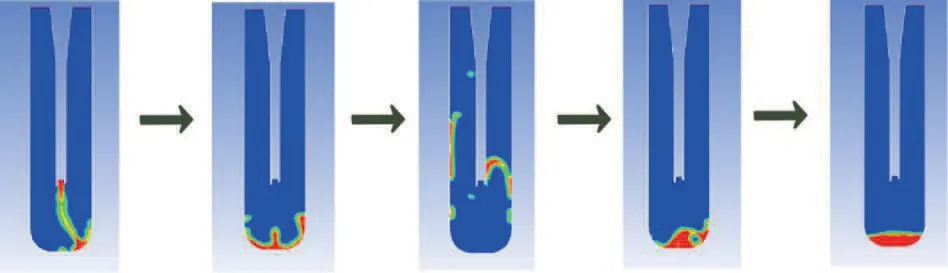
图11 反应杯内流体运动随时间变化示意图

纯化水从针尖注出后，以一定的速度冲击反应杯底部，在反作用力的作用下沿着杯壁向着杯口方向快速运动，最后在重力作用下回落至反应杯底部。

(2)当STEP=0，加样针和反应杯中空气体积占100%；STEP=1，入口两相体积中纯化水的体积设置为100%；STEP=11500时，入口两相体积中空气的体积设置为100%。

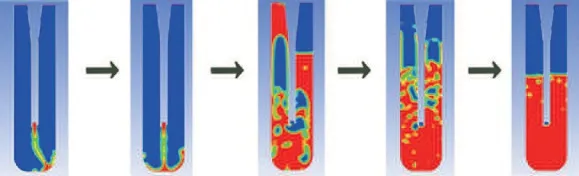
图12 增加纯化水体积后反应杯内流体运动随时间变化示意图

纯化水从针尖注出后，以一定的速度冲击反应杯底部，在反作用力的作用下沿着杯壁朝着杯口方向快速运动，最后在重力作用下回落至反应杯中。由仿真结果可知，部分液体从反应杯中溅出。

通过仿真结果可知，在加样速度不变的条件下，随着纯化水体积的增加，纯化水注入反应杯的稳定性变差，影响加样的精度。

2.2.2 实验验证

搭建实验平台，在加样速度不变的条件下，测试不同体积的液体加样的稳定性。通过实验现象可知，在加样体积较小时，液体无明显的溅液现象；增大加样的体积，有少量液体从反应杯溅出至杯口，并有部分液体粘在反应杯壁上。实验现象显示，在加样速度不变的条件下，随着注出液体体积的增加，纯化水注入反应杯的稳定性变差，影响加样的精度，且实验结果和仿真结果分析一致。实验现象见图13。

图13 实验现象示意图

3 讨论

通过理论计算得到针内流体层流条件下的液体流速区间，仿真模拟加样针内流体的运动特性。层流速度条件下，由于针内壁摩擦力的作用，纯化水的动能不足以克服针内壁的摩擦力，纯化水流沿着针内壁不规则流动，加样针内的空气和纯化水混合在一起，空气未能起到隔离的作用。层流速度条件下，增大加样速度，针内纯化水的流速以抛物线的方式分布，空气起到隔离纯化水和系统液的作用。通过实验验证，层流条件下，通过优化加样速度，液体的定量数据波动范围小且动态特性较稳定，实验结果与理论计算和仿真分析的结果一致。

在加样速度一定的条件下，随着纯化水体积的增加，纯化水注入反应杯的稳定性变差，影响加样的精度。通过实验验证表明，实验结果和仿真结果分析一致。

本研究采用流体仿真软件，以纯化水为研究介质，采用流体仿真的方法复现实际加样的过程，并结合理论分析和实验结果，分析加样速度与加样量等因素对加样过程的动态特性的影响，为微量液体高精度加样提供理论支持。实际应用中反应杯内壁存在一定的粗糙度，且反应杯内壁存在一定的挂液现象，因此，有必要对反应杯内壁挂液的现象做进一步研究，验证挂液现象对生化分析仪测试结果的影响。