基于熵权改进模糊综合评价模型的大气质量评价
2020-04-01蒋鹏飞
蒋鹏飞
(三峡大学 水利与环境学院,湖北 宜昌 443002)
近年来,我国经济快速发展的同时出现了大气环境日益恶化的问题,它直接影响着人类的生存和发展,因而成为公众的关注焦点。根据实测结果对大气质量进行客观评价,对正确认识大气环境污染现状并有效控制、治理具有重要意义。城市大气环境是一个复杂的系统,时空变化性很强,存在很多未确知因素[1]。大气环境质量评价经过近几十年的发展,众多学者提出了不同的评价方法:赵晓亮[2]提出结合聚类分析与层次分析法分别实现关联函数逻辑域的值域拓展与特征权重的确立,完成可拓论模型的改进,并应用于大气质量的评价研究;赵东洋[3]建立改进属性识别模型,该模型结合属性识别理论模型,同时运用变异系数法计算权重,从而对属性识别的评价模型进行改进,并与综合污染指数法和模糊综合评价法进行了结果比较,阐述了该方法与这两种方法的优点和对大气质量进行优劣排序;王博[4]将基函数应用于人工神经网络,并用专家评分后归一化处理的方法对输入层的权值初始值进行优化,建立了优化的小波神经网络模型,为大气质量评价提供一种新的思路和方法;王瑛[5]采用改进CRITIC法和超标倍数法的集成权重对评价指标进行客观赋权,再结合模糊优选法对大气质量进行综合评价。
本文基于传统模糊综合评价常见的几种方法:乐观型、悲观型、结合型以改进形成一个新的混合矩阵,使用熵权法确定指标权重;考虑到各决策方法的隶属度相对集中,采用变异系数法确定其权重,该模型能够更好体现各指标优势和评价方法优势,这样使评价结果更科学合理。
1 改进模糊综合评价模型
1.1 指标体系的处理
在大气环境质量评价中,为了充分体现各评价指标的相对性,可对其进行归一化处理:
(1)
1.2 评价模型[6]
选择模糊综合评价作为大气环境质量评价的方法,设评价对象为:A={a1,a2,…,an},ai为评价因子i=(1,2,…,n),n为评价因子的个数。设定性指标评语等级为B=[b1,b2,…,bn]。以评价指标在整体上对各等级的隶属关系可构建如下矩阵:
(2)
1) 对于模糊综合判断矩阵C,在其中取最大值作为判定依据,等同于按乐观型决策原则,可得:
C1=[cij,cij,…,cij]
(3)
2) 在C中取最小值作为判定依据,等同于按悲观型决策原则可得:
C2=[cij,cij,…,cij]
(4)
3)在中C取均值作为判定依据,等同于按结合型决策原则可得:
C3=[cij,cij,…,cij]
(5)
式(3)-式(5)中:cij为i从1到m的最大值、最小值、均值,i=(1,2,…,m),j=(1,2,…,n)。
结合以上3种原则可得由C1,C2,C3组合的混合判断矩阵:
(6)
上述矩阵综合了3种决策思想,可以称之为混合矩阵。通过以上分析,可以利用矩阵W与单个指标评价的模糊关系矩阵C′相乘得到矩阵E:
E=WC′
(7)
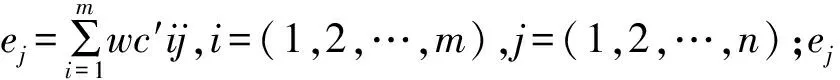
1.3 决策方法权重的确定
3种不同的决策思想在整体上的隶属度是不同的,对各等级的隶属度相对集中,故采用变异系数法[7]确定权重。
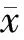
(8)
(9)
2) 根据上述计算结果,求各决策指标的变异系数。由变异系数的定义:变异系数为标准差与平均数之比,设变异系数为Vi,则:
(10)
式中:i=(1,2,…,e)。
3) 对Vi进行归一化处理,得到各决策指标的权重Qi:
(11)
4) 根据权重的计算结果和原始指标数值,计算出各观测对象的整体隶属度Z:
(12)
2 评价指标权重的确定
针对大气环境质量评价,采用熵权法[8]确定各评价指标的权重。在信息论中,熵值反映了信息的无序化程度,可以用来度量信息量的大小。某项指标携带的信息越多,表示该指标对决策的作用就越大;熵值越小,则系统的无序度越小,故可用信息熵评价所获系统信息的有序度及其效用,即由评价指标值构成的判断矩阵来确定指标的权重,从而尽量消除各指标权重的人为干扰,使评价结果更符合实际[9]。计算步骤如下:
1) 构建由m个评价对象n个指标的矩阵R=(rij)m×n,i=(1,2,…,n),j=(1,2,…,m)。
2) 将矩阵R归一化处理得到矩阵B。
(13)
式中:rmin,rmax分别为同一评价指标下不同对象中的最小值和最大值。
3) 确定评价指标的熵值:
(14)
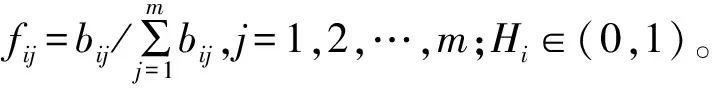
显然,当fij=0时lnfij无意义,因此需对fij加以修正,将其定义为:
(15)
4) 根据熵值求得熵权。
W=(wi)1×n
(16)
(17)
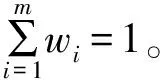
3 实例分析
空气质量的好坏反映了空气污染程度,它是依据空气空污染物浓度的高低来判断的。综合考虑SO2、NO2、PM10、CO、O3、PM2.5等6种污染物浓度对宜昌市上半年空气质量进行研究,其数据见表1,根据式(1)进行数据量化处理并作单因素评判矩阵得到模糊关系(表2)。

表1 宜昌市上半年评价指标数据表Tab.1 Evaluation index data table of Yichang in the first half year
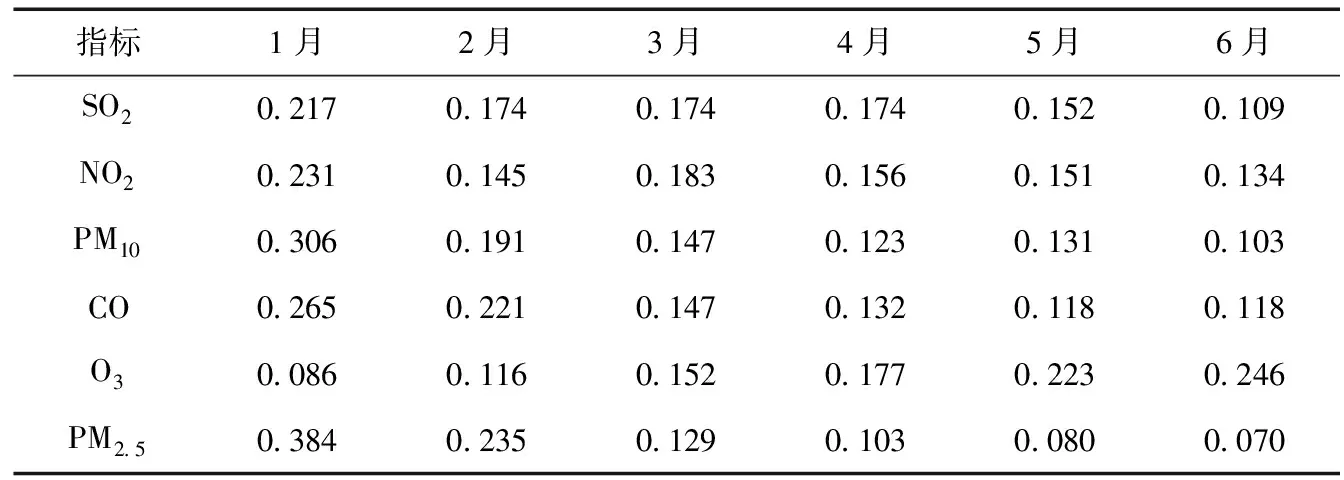
表2 宜昌市上半年评价指标数据归一化表Tab.2 Normalization table of evaluation index data of Yichang in the first half year
3.1 熵权法确定指标权重
各评价指标的实际值由式(13)构造归一化判断矩阵如下:

利用式(14)、式(15)求得各评价指标的熵值,见表3。利用式(16)、式(17)可得到各指标熵权值,见表4。
3.2 变异系数法确定决策方案权重
利用式(2)-式(6)可得决策目标矩阵,见表5。
利用式(8)-式(11)可得各方案权重,见表6。

表3 各评价指标熵值Tab.3 Entropy value of each evaluation index

表4 各评价指标熵权值Tab.4 Entropy weights of each evaluation index

表5 决策目标矩阵数据表Tab.5 Decision objective matrix data table

表6 决策方案权重表Tab.6 Decision scheme weight table
3.3 计算隶属度
利用式(7)、式(11)计算各月份隶属度,1-6月份隶属度分别为:0.253 6,0.182 7,0.158 3,0.144 4,0.155 3,0.157 4,故大气污染程度排序为:1月、2月、3月、6月、5月、4月。鉴于城市环境短期内变化相对有限,城市空气污染状况实际上是由污染源和气象条件这两个内外因素共同决定的[10]。1月份受系统性逆温控制,逆温持续时间长,空气扩散条件长期维持不利,且受外源性污染输入影响的可能性较大,市大气重污染应急指挥部起启动Ⅲ级(黄色)预警应急响应,落实强制性污染减排措施。4月份气象条件改善,有利于污染的扩散;强制减排使内源性污染源减少。由此可见,评价结果与实际相符。
4 结 语
1) 采用熵权法确定评价指标权重,避免了凭经验确定指标权重的主观随意性,该方法能够处理多指标决策的不相容问题,有良好的辨析能力。
2) 以隶属度大小来判断各评价对象的优劣,该模型思路清、通俗易懂,不需要做过多的运算,就能得到较为可靠的结果,实用性较强。
3) 建立大气环境质量评价体系。基于传统模糊综合评价模型加以改进,使评价结果贴切实际,表明该模型用于解决该问题的可行性。
