高温质子交换膜燃料电池电堆端板拓扑优化
2020-04-01王浩然,吴私,杨林林,兰海兵,陈超,孙伟,宋学官*
王 浩 然, 吴 私, 杨 林 林, 兰 海 兵, 陈 超, 孙 伟, 宋 学 官*
( 1.大连理工大学 机械工程学院, 辽宁 大连 116024;2.中国科学院大连化学物理研究所 洁净能源国家实验室, 辽宁 大连 116023 )
0 引 言
高温质子交换膜燃料电池是一种新型的将燃料中的化学能转化为电能的清洁发电装置,其工作温度通常在100~200 ℃.这种电池由于具有较高的能量转换效率、较快的启动速度、较低的工作温度、较小的工作噪声、较长的工作时间与较少的污染产物等特点而备受关注[1-2].在实际的应用中燃料电池产品包含了许多串联的单电池用来提高总电压与总功率.燃料电池由阴极板、阳极板、膜电极、密封垫圈、端板等部件组成.通常来说,燃料电池端板用来提供适当的装配荷载以保证整个装备的密封性.端板通过一系列螺栓或者其他紧固装置连接各单电池形成稳定的电堆结构,并且将装配荷载均匀地传递到电堆内各部件中[3].
一般来说,如果装配压力过小将导致气体扩散层压缩量过低,电堆内部存在较高的接触电阻.如果装配压力过大,气体扩散层的渗透性将会变小,影响燃料气体的传输[4].除此之外,预紧力分布不均也会导致燃料气体分配不均,影响电流密度的分布,最终降低电池的运行寿命[5].从设计的角度来看,可以通过增加端板的厚度简易地实现其高刚度[6].但是过厚的端板将会导致整个系统的质量与体积过大.为了同时实现端板的高刚度、低质量,提出了例如肋型、炸弹型或弓型等较为复杂的端板结构.Yu等[7]在端板的内表面设计了一个预弯曲结构,使其在施加荷载后变形成为一个平面,从而使得端板上的压力尽可能均匀.虽然多数端板的设计看起来相当有效,但是基于拓扑优化的端板结构可以使设计人员在特定的约束条件下找到给定目标下的最优拓扑布局.Fly等[8]提出了燃料电池电堆的一维等效刚度模型,能够很好地预测在施加外部荷载时的接触压力.Lin等[9-10]建立了在弹性单元下的力学等效刚度模型,用来研究结构参数对端板应力分布的影响,并且建立了一种具有非线性接触的质子交换膜燃料电池电堆端板多目标拓扑优化模型.Liu等[11]在二维形状优化和改进拓扑优化的基础上,采用几何参数化方法得到了三维优化拓扑,使得在端板轻量化的同时接触压力分布均匀.Wang等[12]提出了在端板上集成一个液压装置用来提高压力在端板上的均匀性.
本文针对燃料电池端板对电堆的影响,综合考虑端板的体积质量、封装荷载、工作温度、接触压力在单电池内的均匀性以及接触压力在单电池之间的一致性等问题,应用Ansys Workbench有限元软件对电池端板结构进行拓扑优化设计.
1 模型说明
1.1 几何模型
本文研究的高温质子交换膜燃料电池共包含100级单电池,研究模型十分庞大,因此需对模型进行简化,用来减少计算量,从而减少计算时间.以下为本文中的一些基本假设与基本简化思路.
(1)由于双极板中的平行流道较为密集,且双极板与质子交换膜之间接触压力的分布与平行流道几乎无关,同时根据等效刚度模型理论,双极板的平行流道对结构等效刚度影响较小,因此本文中的双极板可以看作一张无流道的薄板,用来减少接触对的数量并降低模型复杂程度.
(2)由于本文研究工作时电堆的受力情况,不考虑持续产生的反应热与冷却流道实时的散热,本文中热分析仅为三维恒定温度场.
(3)仅考虑在装配完成时整个电堆内部的接触压力,所以只需要在非线性材料中的应力-应变曲线中找到对应工况下的弹性模量并将其线性化处理.
(4)燃料电池电堆在预紧力的作用下主要产生在厚度方向上的压缩位移,因此在考虑材料热膨胀的时候忽略其余两方向的变形,用于模型材料的简化.
(5)本文研究的电堆由4根螺栓进行连接,无论在x、y、z方向该结构都是完全对称的,因此为了减小模型、减少计算量,将电堆进行对称处理(取1/8模型进行分析).
含有两级单电池的1/4电堆模型如图1所示.
1.2 有限元网格与材料属性
多区域网格剖分方法可以保证网格的离散程度较为均匀,在设计域中规则几何区域与复杂几何区域使用不同的网格类型进行剖分能极大程度保证计算精度和效率.同时还需要对结构进行网格无关性验证.本文应用Ansys Workbench进行网格剖分,采用四面体、六面体结合的方式剖分网格,网格数量在24万左右,节点数控制在100万左右.
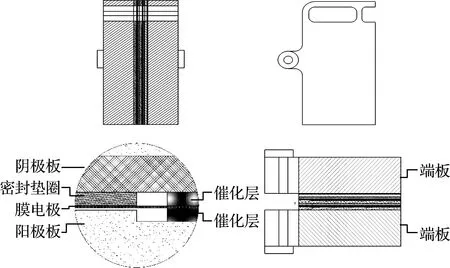
图1 含有两级单电池的1/4电堆模型
电堆中阴、阳极板采用石墨板材料,气体扩散层采用碳纸材料,质子交换膜采用PBI材料,密封垫圈采用橡胶材料,绝缘垫片采用聚苯醚材料,电堆端板采用铝合金材料,所有材料都假设为各向同性的线弹性材料,各种结构的材料属性均在表1中列出.需要说明的是,根据等效刚度模型[13],密封垫圈的弹性模量是通过对橡胶材料的应力-应变曲线进行线性拟合得到的.质子交换膜的材料属性如弹性模量等都与温度和湿度相关,但在本文的分析中不考虑温度与湿度在质子交换膜上分布的影响,但是考虑了常温(25 ℃)与正常工作温度(160 ℃)时的弹性模量.由于电堆主要的变形在厚度方向上,热膨胀系数仅在厚度方向上有效.
1.3 边界条件
首先根据x、y、z3个方向完全对称的电堆结构,有限元仿真时对3个对称面采用对称约束,不仅防止电堆发生刚体位移,同时减少7/8的计算时间.为使端板与电池之间接触压力均大于零,除了端板与第1层密封垫圈、碳纸之间的接触外,其余各部件之间所有接触面都设置为bonded接触(第1层端板与两材料的接触设置为rough接触),因此该有限元模型将具有非线性因素.对于温度场的有限元计算而言,将端板外表面的对流换热系数设置为5×10-6W/(mm2·K).根据工作时温度简化,在不考虑反应热与冷却条件下将电堆内部除端板、绝缘垫片以外所有部件温度均设置为160 ℃(工作前的环境温度设置为25 ℃).对于结构力学场的计算而言,由于设置了3个方向的对称,已经进行了刚体约束,因此仅需要在绝缘垫片处施加装配荷载即可,本文研究的工况为施加1 t的预紧力即在重力加速度为9.8 N/kg下9 800 N的装配荷载在端板上.本文只取了1/8模型进行研究,因此加载在绝缘垫片上的荷载为竖直指向电堆内部的2 450 N.
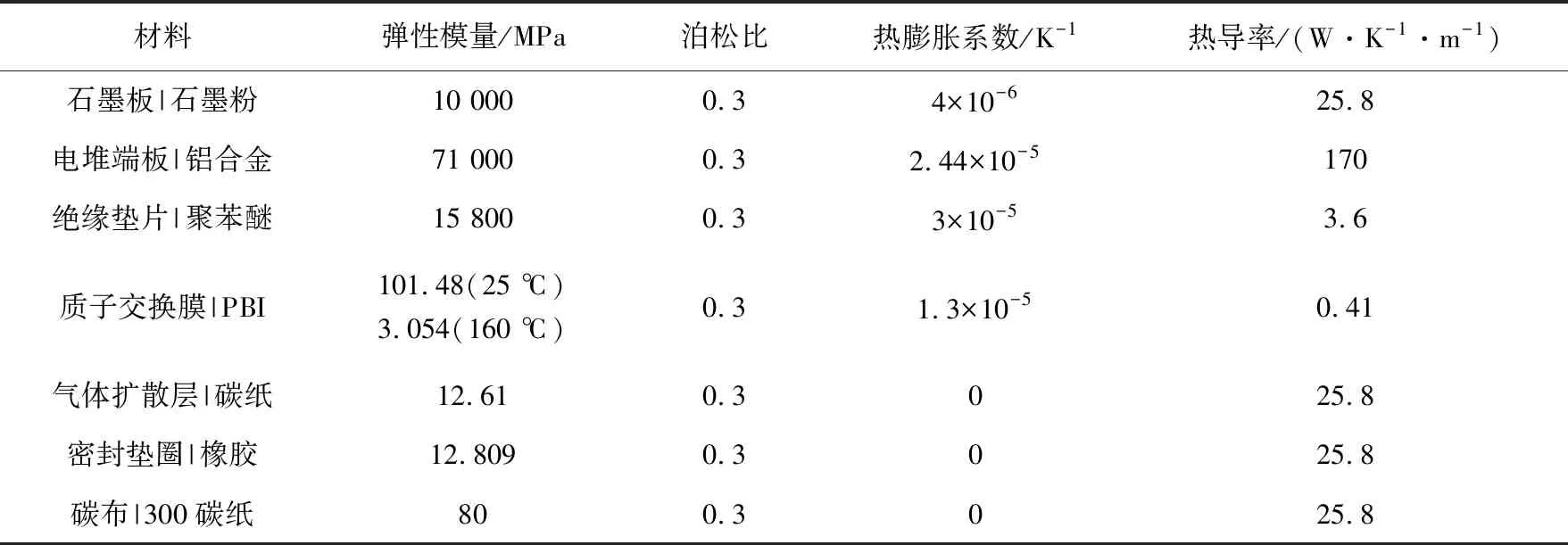
表1 材料属性
1.4 拓扑优化与优化设计参数
为了更好地了解端板的结构设计,本文将结构的拓扑优化与端板的设计相结合.常用的连续体拓扑优化方法有均匀化方法(HM)、独立连续映射法(ICM)、变密度法(VDM)与变厚度法(VTM)等.本文基于变密度法对燃料电池端板进行拓扑优化,使用的插值模型为SIMP法,其表达式为
(1)
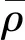
拓扑优化模型基于图2(a)所示的端板结构,在进行拓扑优化之前,需要确定优化区域.初始设计区域应尽可能大,以保证有足够的空间进行优化.优化时需要排除螺栓孔、必要的框架与支撑的周边区域.在本文的研究中,为保证夹紧装置与密封性,端板的优化区域为图2(a)中蓝色区域.同时以端板质量最小化为优化目标,将端板中的最大应力不大于16 MPa作为约束条件,具体如下式所示:
Find:
ρ∈Ω
Obj:
min (ρ×V)
(2)
s.t.
σmax≤16 MPa
其中ρ为密度,Ω为设计空间,V为体积,σmax为端板所受的最大应力.
采用热力耦合分析结构拓扑优化过程中的约束条件,端板有效区域(蓝色区域)的接触压力为0.418 MPa,其余区域所受的接触压力为0.423 MPa,同时固定4个绝缘垫片.为了使拓扑结果更加有说服力,网格的剖分应较为细致.为了在厚度方向进行充分拓扑,本次研究中在厚度方向剖分了9层网格,并且所有网格均设置为六面体网格.整个端板共有42 834个网格,1 900 081个节点,网格示意图如图2(b)所示.在迭代计算过程中设置迭代步数为500,残差为1×10-3.
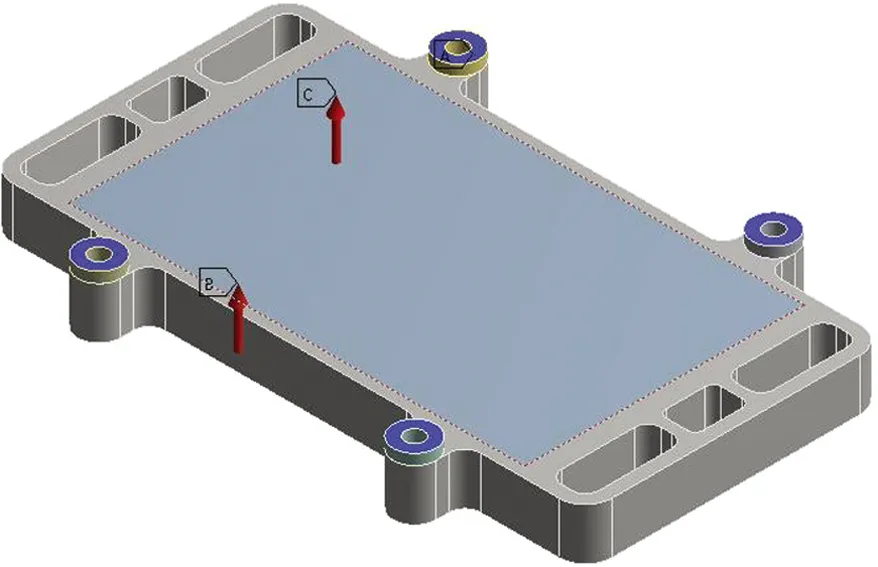
(a) 拓扑优化的约束条件

(b) 网格剖分示意图
1.5 评价指标
电堆接触压力的评估可以分为两个方面,即压力大小与均匀性.两者都受到质子交换膜燃料电池端板的结构与装配荷载的影响,并且接触压力的大小与均匀性严重影响着高温质子交换膜燃料电池的内部燃料气体与温度的分布情况,进而影响质子交换膜燃料电池的工作性能.接触压力的大小影响整个电堆装置的密封性能与各零件的使用寿命,接触压力的均匀性影响着质子交换膜、扩散层与催化层压缩程度的均匀性,进而影响单电池的发电效率.
质子交换膜与双极板之间接触压力的标准差可以明显地表现出接触压力分布的均匀程度[14];平均值可以反映出接触压力大小的平均幅度.两者的比值称之为变异系数,可以更好地表现出接触压力的均匀性,并且是一个量纲一的性能指标.
(3)
(4)
(5)
其中σ为标准差,E为平均值,Cv为变异系数.变异系数越大,均匀性越差.
2 拓扑优化结果
拓扑优化的结构通常由单元相对密度表示,在去除了具有低密度的单元后,优化所得结构如图3(a)所示.与原始端板相比,拓扑优化后的结构降低了很大部分的质量.考虑装配难度与制造难度,还需对优化后的结果进行重新设计,得到如图3(b)、(c)所示的端板拓扑结构.为降低连接处的应力集中对其进行倒角处理.

(a) 拓扑结构
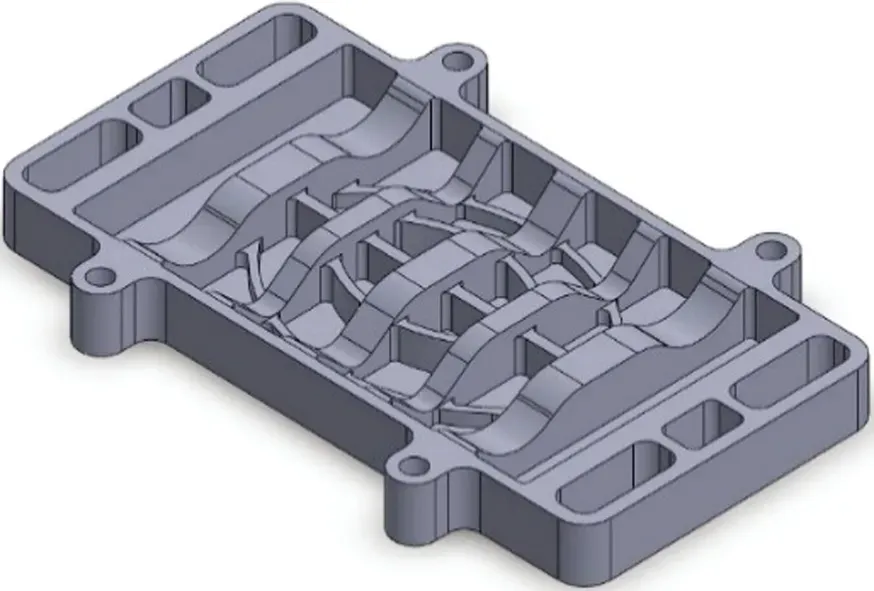
(b) 新结构1

(c) 新结构2
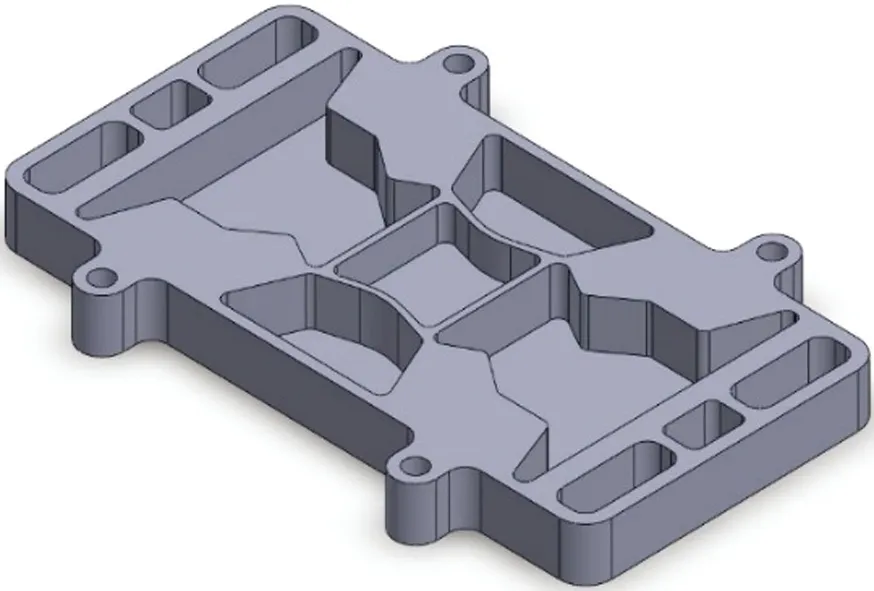
(d) 现结构
如表2所示,目前使用端板质量为592.79 g,未进行轻量化前的结构为1 050.02 g,对比可见,所有结构在拓扑前后具有较大程度的改变.不过对比现有端板,新结构1质量降低了3.74%,新结构2质量降低了18.62%,由此可见仅考虑质量的情况下端板的优劣顺序为新结构2>新结构1>现结构.
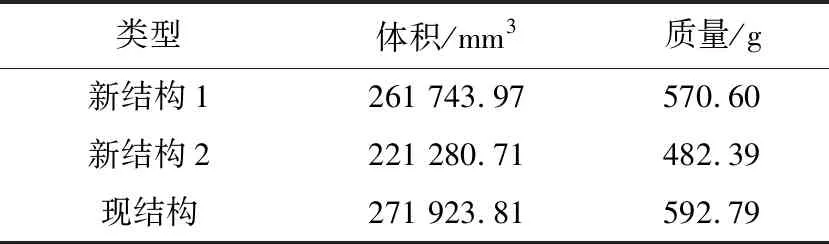
表2 不同结构的体积与质量
3 仿真结果对比与分析
根据上文设置边界条件下取1/8模型计算,端板与下层结构接触压力云图如图4所示.
根据仿真结果计算端板下表面接触压力的平均值、标准差与变异系数,结果如表3所示.由于燃料电池的装配荷载在靠近端板的层间所引起的压力不均匀性较严重,本文首先对首层接触压力进行研究.根据表3可知,现有端板的变异系数为0.841,在新设计的两种端板中,新结构1、2的变异系数分别降低了2.62%与0.71%.可见新设计端板接触压力的均匀性均有所提高,其中新结构1的均匀性最好.
根据图4的接触压力云图可见,有效区域的接触压力与密封区域的接触压力相差很大,同时还可以发现将密封区域与电池区域的接触压力同时分析是不合理的.表3分析的变异系数为整个接触面共同分析计算,将密封区域与有效区域的接触压力共同取平均值,其值的大小并不能反映电池有效接触压力的大小,算得的标准差也不能准确地反映单电池中有效区域的接触压力离散程度,其值大于正常值.因此为准确地评价电堆的好坏,有必要提取有效区域的接触压力即电池的双极板与膜电极之间接触压力,本文计算提取了图4所示的50层双极板阳极与质子交换膜之间的接触压力云图.
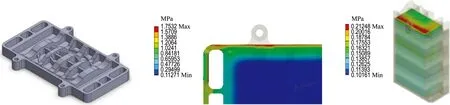
(a) 新结构1示意图、端板下表面接触压力云图、质子交换膜与阳极板之间接触压力分布云图
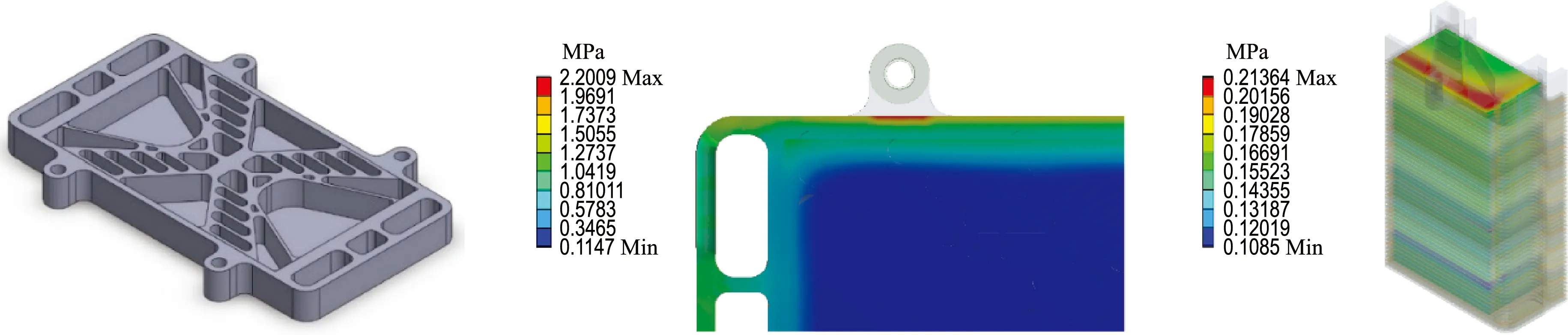
(b) 新结构2示意图、端板下表面接触压力云图、质子交换膜与阳极板之间接触压力分布云图
(c) 现结构示意图、端板下表面接触压力云图、质子交换膜与阳极板之间接触压力分布云图
图4 结构示意图及有限元分析结果
Fig.4 Schematic diagram and finite element analysis results
表3 端板下表面接触压力的平均值、标准差及变异系数
Tab.3 Average value, standard deviation and coefficient of variation of contact pressure on the lower surface of end plate
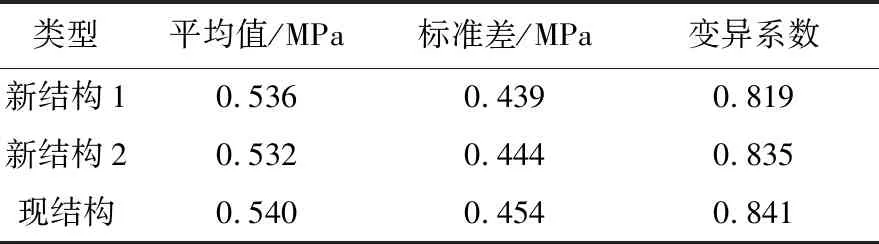
类型平均值/MPa标准差/MPa变异系数新结构10.5360.4390.819新结构20.5320.4440.835现结构0.5400.4540.841
提取有限元计算结果,计算50层所有单元的变异系数计算结果如表4所示.可见现有端板的变异系数为0.078 9,比较两种新设计结构的变异系数,新结构1的均匀性相比于现有端板提高了10.90%,新结构2的均匀性相比于现有端板提高了0.25%,结果表明新结构1端板将使整个装配压力在电堆中分布得更加均匀.
表4 所有阳极有效区域接触压力的平均值、标准差与变异系数
Tab.4 Average value, standard deviation and coefficient of variation of contact pressure of all anode effective area
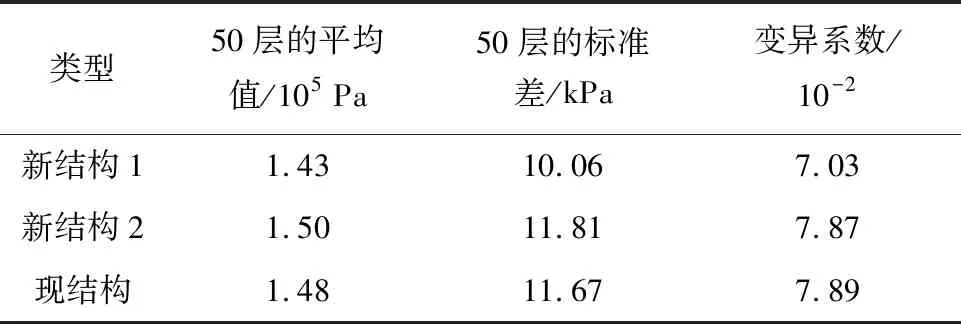
类型50层的平均值/105 Pa50层的标准差/kPa变异系数/10-2新结构11.4310.067.03新结构21.5011.817.87现结构1.4811.677.89
除了考虑接触压力的均匀性外,单电池之间接触压力的一致性也是评价电堆性能的指标之一,表5为3种端板装配电堆每层接触压力变异系数的标准差,现有端板变异系数的标准差为0.017 6,由于标准差越小每层接触压力的一致性越好,在以下两组新端板中,新结构1与新结构2的变异系数的标准差分别为0.012 3与0.013 5,均小于现有端板的变异系数的标准差.其中新结构1的一致性提高了30.11%,新结构2的一致性提高了23.30%,可见端板新结构1为所有新设计端板中一致性最好的一组.
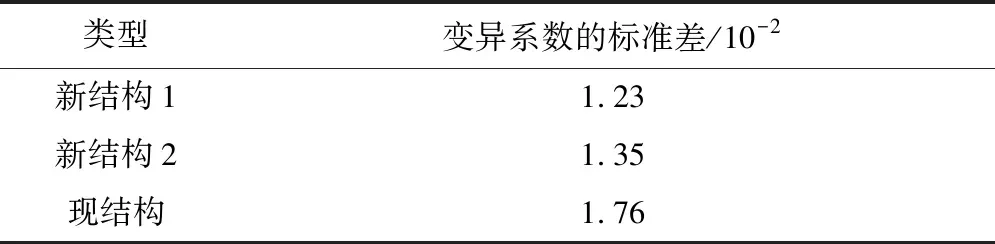
表5 每层接触压力变异系数的标准差
根据以上计算结果可知,新设计的端板新结构1、2与现有端板结构相比较,均匀性与一致性均有提高,同时新结构1是新设计的两种端板中接触压力分布最均匀、一致性最高的结构.
4 结 论
(1)在高温质子交换膜燃料电池几何模型的基础上,综合考虑电堆结构的形状、电堆内部单电池的受力情况、不同材料的属性与材料分布情况,同时还考虑紧固装置对电堆预紧力的影响,构建了一种燃料电池电堆的简化模型.
(2)以提高电堆整体的发电效率为目的,综合考虑整体的装配荷载,构建了一种不仅考虑单电池内接触压力的均匀性,同时还考虑各单电池之间接触压力一致性的电堆性能评价指标.
(3)通过拓扑优化方法优化得到的燃料电池端板结构,相较于现有端板结构,质量降低了3.74%,均匀性提高了10.90%,一致性提高了30.11%.因此拓扑优化可以为端板的优化设计提供理论基础.
