磁驱动单侧飞片实验的数值模拟*
2020-04-01阚明先王刚华段书超张朝辉
阚明先,王刚华,肖 波,段书超,张朝辉
(中国工程物理研究院流体物理研究所,四川 绵阳 621999)
自1999 年美国Sandia 国家实验室利用Z 装置进行了平面等熵压缩和飞片发射实验以来,磁驱动飞片技术取得了飞速发展。Knudson 等[1]采用限制飞片加载磁压的方法,获得了20 km/s 的飞片速度。Lemke 等[2]采用斜波加载的方法,获得了45 km/s 的飞片速度。磁驱动飞片技术有助于材料的状态方程、高能量密度物理和武器物理等的研究[1-5]。随着磁驱动飞片实验的开展,磁驱动飞片理论也取得了许多进展。Lemke 等[6]利用磁流体力学方程和边界磁场公式 B=μ0I(t)/S ( B 是磁场强度, μ0是真空磁导率,I(t) 是电流,S 是自由参数),对磁驱动飞片实验进行了模拟;Lemke 等[7]把磁驱动边界磁场公式改进为B= fμ0I(t)/(g(t)+W(t)) (f 为电流有效系数,g(t)为阴阳极之间的间隙,W(t)为电极板的宽度)。采用上述两个磁场边界公式,必须从实验测量电流调整后的模拟电流出发,磁流体力学程序才能模拟出与实验一致的自由面速度历史;从实验测量电流直接模拟磁驱动飞片实验,模拟的飞片自由面速度在实验后期总是比实验测量结果偏大[2,6-8]。Kan 等[9]考虑了飞片厚度方向上的熔化情况,指出飞片的电流加载面不是飞片电流加载端的端面,而是飞片电流加载端的熔化面,在磁驱动飞片磁场边界公式中增加了飞片电流加载端厚度方向上的熔化宽度 gm(t) ,提出了新的磁场边界公式 B = fμ0I(t)/(g(t)+gm(t)+W) ,解决了从实验测量电流直接模拟磁驱动飞片实验的问题。
根据文献[9],磁驱动飞片发射实验从实验测量电流正确模拟实验测量速度,需要考虑阴、阳电极的运动情况和阴、阳电极厚度方向上烧蚀宽度的影响;否则,数值模拟速度与实验测量速度将不一致,在磁驱动实验后期,数值模拟速度总是比实验测量速度偏大。对于磁驱动单侧飞片或对称飞片实验,由于阴、阳电极都是金属材料,因此阴、阳电极电流加载端都将被烧蚀,阴阳电极电流加载端的熔化宽度将随时间的增加而增大,所以应该采用双侧飞片模型进行数值模拟。然而,磁驱动单侧飞片或对称飞片实验事实上都可不考虑厚的电极(阴极)的运动情况和烧蚀宽度的影响,可采用单侧计算模型进行模拟,并且模拟的飞片自由面速度与实验测量结果一致[6],这是个问题。在本文中,对聚龙一号装置上的磁驱动单侧飞片实验建立双侧计算模型,并对模拟结果进行研究分析,解释磁驱动单侧飞片实验可以采用单侧计算模型模拟的原因,可为磁驱动单侧飞片实验的单侧计算建模提供理论依据。
1 实验配置
聚龙一号装置是中国工程物理研究院流体物理研究所研制的超高功率、多路并联运行的大电流脉冲装置[10]。该装置具有同步放电和波形调节等两种工作模式。同步放电模式的输出脉冲前沿约90 ns,最大输出电流8~10 MA;波形调节模式的输出脉冲前沿200~550 ns,最大输出电流5~7 MA。聚龙一号装置已用于Z 箍缩、磁驱动高速飞片发射和磁驱动冲击压缩/准等熵压缩等磁驱动实验[11-13]。
聚龙一号装置的磁驱动单侧飞片发射实验的负载结构示意图如图1 所示。C、A 分别为磁驱动单侧飞片实验中的阴极和阳极,W 为阴、阳电极的宽度。阴、阳电极为长方体铝材料,阳极上嵌入方形、圆形或椭圆形飞片。阳极上嵌入的是长方形飞片,h 为飞片的高度, δf、 δc分别为飞片和阴极的厚度, g0为阴阳电极之间的初始间隙。PTS-061 实验的飞片为长方形,PTS-064 实验的飞片为椭圆形。采用激光速度干涉仪(VISAR)测量飞片的速度历史。聚龙一号装置的磁驱动单侧飞片发射实验的负载参数,见表1。

图 1 PTS-061 实验的磁驱动负载结构Fig. 1 Cross section of 3D flyer configuration

表 1 磁驱动单侧飞片实验的负载参数Table 1 Loading parameters for magnetically driven one-sided flyer plate experiments
2 物理模型
磁驱动实验采用磁流体力学程序模拟,本文中采用二维磁驱动数值模拟程序MDSC2 模拟磁驱动实验。MDSC2 程序是中国工程物理研究院流体物理研究所研制的磁流体力学程序[14-15],已用于固体套筒内爆、磁驱动飞片发射实验的数值模拟研究[9,16-18]。MDSC2 程序求解的磁流体力学方程组为:
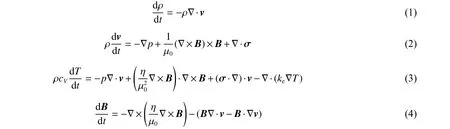
式中:ρ 为密度,T 为温度,v 为速度,B 为磁感应强度,t 为时间, η 为电阻率[19], p 为压强, σ 为人工黏性张量, ke为热扩散系数, cV为比热容, μ0为真空磁导率,d/dt 为Lagrangian 导数。
对于磁驱动飞片,加载面上的磁压力为:

式中: B0为飞片加载面上的磁感应强度[9]。 B0为:

在磁驱动飞片实验中,电流有效系数f 由包含电极的负载结构决定,与飞片的初始厚度、阴阳电极的初始宽度、阴阳电极的初始间隙大小有关。在MDSC2 程序中,由Lindermann 熔化线判断物质的熔化情况,从而计算飞片的烧蚀宽度 gm(t) 。
3 数值模拟
对于磁驱动单侧飞片实验,通常采用单侧计算模型进行模拟。单侧计算模型不考虑阴极板的烧蚀和运动情况,假定在实验过程中阴极板的电流加载面始终保持不动,阳极上的飞片在洛仑兹力的作用下向阴极板相反的方向运动。在单侧计算模型中,只对飞片进行模拟,阴极板不参与模型计算。单侧计算模型示意图如图2 所示。图2 中, g0是阴阳极板之间的初始间隙,dfl为飞片电流加载端端面的位移, gmf为飞片厚度方向上电流加载端的熔化宽度(即式(6)中的gm(t) ), dfl+gmf为飞片的电流加载面的位移, g0+dfl为式(6)中飞片与阴极之间的间隙 g (t) 。
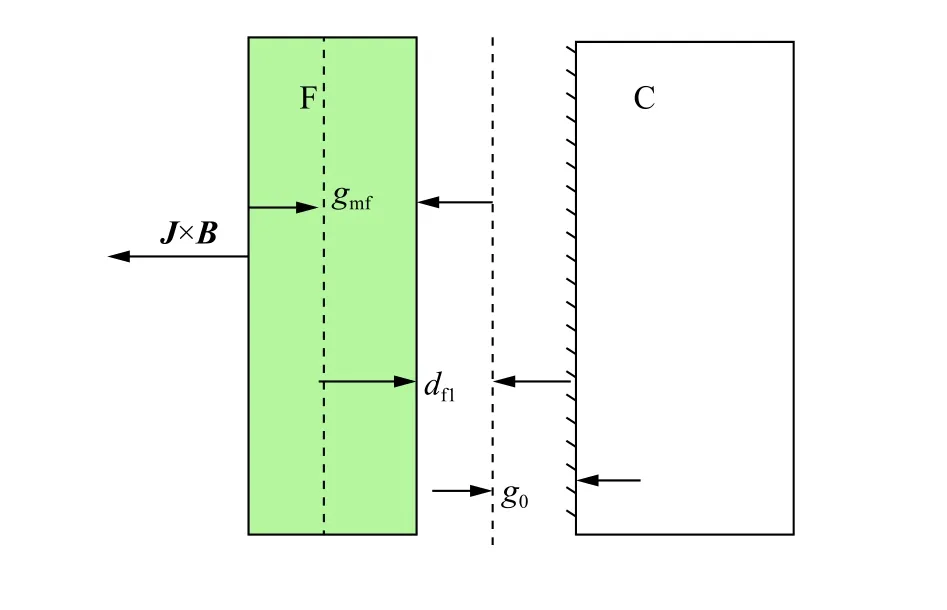
图 2 单侧计算模型Fig. 2 One-sided computational model
采用单侧计算模型,对PTS-064 磁驱动单侧飞片发射实验进行了模拟。采用50×100 的网格进行模拟(下同)。图3 为PTS-064 实验的实验测量电流。图4 为单侧计算模型的飞片自由面速度(f=0.77)。由图4 可知,单侧计算模型模拟的飞片自由面速度与实验测量的飞片速度一致。单侧计算模型能正确模拟PTS-064 实验磁驱动单侧飞片的自由面速度。图5 为飞片与阴极之间的真空间隙 g (t) 和飞片烧蚀宽度 gm(t) 的比较。由图5 可知,飞片烧蚀宽度随着时间持续增大,在后期,飞片烧蚀宽度和阴阳极间的真空间隙对确定边界磁场强度同样重要。在测量结束时,飞片烧蚀宽度对边界磁场强度的影响为13.8%,飞片烧蚀宽度在PTS-064 单侧飞片实验的数值模拟中不能忽略。

图 3 PTS-064 实验的电流Fig. 3 Current of experiment PTS-064

图 4 PTS-064 实验飞片自由面速度的单侧计算结果Fig. 4 Flyer plate free-surface velocities of experiment PTS-064 simulated by one-sided computational model
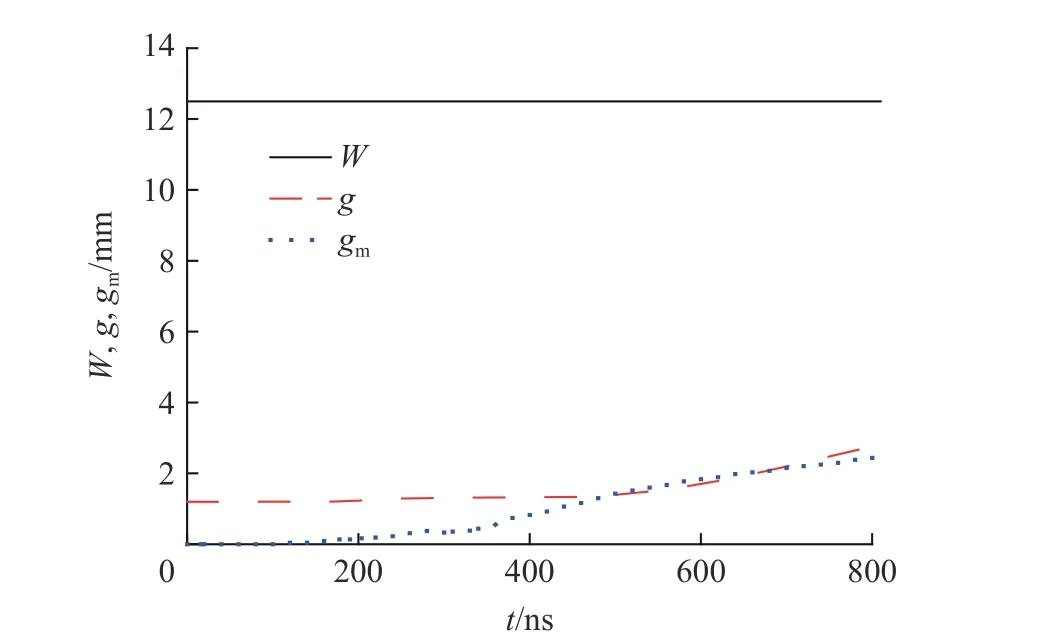
图 5 PTS-064 实验真空间隙和飞片烧蚀宽度的单侧计算结果Fig. 5 Vacuum gap and flyer-plate ablation depth of experimentPTS-064 simulated by one-sided computational model
在PTS-064 单侧飞片实验中,飞片厚度方向上的烧蚀宽度对边界磁场的影响较大,数值模拟时不能忽略。然而,阴极在实验中同样将被烧蚀,那为何单侧计算模拟可以不考虑阴极厚度方向上的烧蚀宽度。为此,采用双侧计算模型对PTS-064 单侧飞片实验进行模拟。双侧计算模型不仅要考虑飞片厚度方向上的烧蚀和运动情况,而且要考虑阴极厚度方向上的烧蚀和运动情况。磁驱动单侧飞片实验的双侧计算模型示意图,如图6 所示。图6 中, g0为阴阳极板之间的初始间隙, dfl为 飞片电流加载端端面的位移,dcl为阴极电流加载端端面的位移, gmf为飞片电流加载端的熔化宽度, gmc为阴极电流加载端的熔化宽度。显然, dfl+gmf为飞片电流加载面的位移, dcl+gmc为阴极电流加载面的移动距离, g0+dfl+dcl为式(6)中飞片与阴极之间的间隙g (t) ,gmf+gmc为式(6)中飞片与阴极电流加载端厚度方向上熔化宽度之和 gm(t) 。
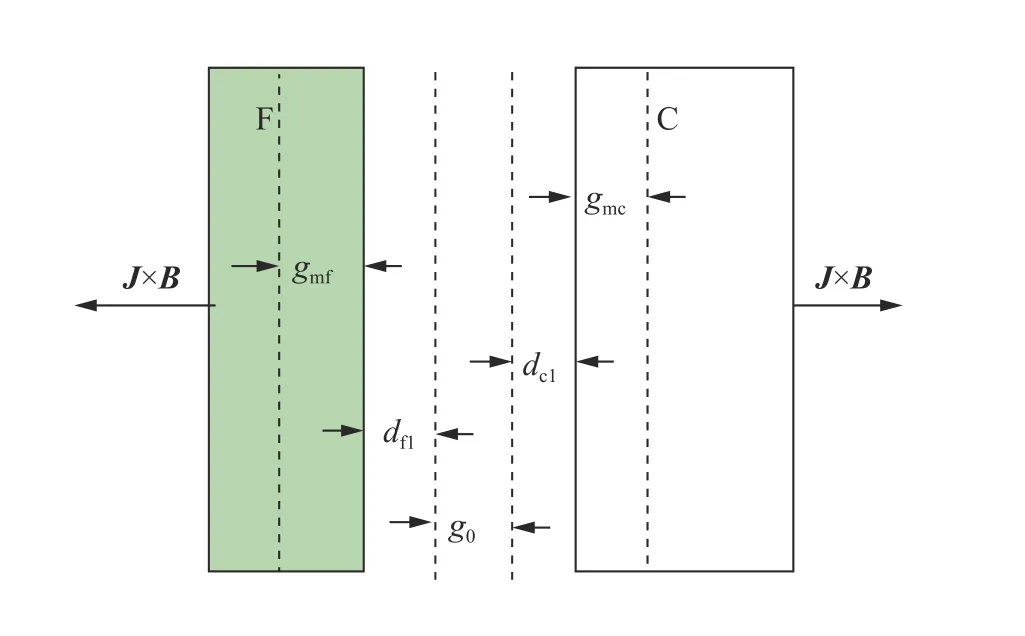
图 6 双侧计算模型Fig. 6 Two-sided computational model
采用双侧计算模型对PTS-064 磁驱动单侧飞片发射实验进行了模拟。飞片和阴极都采用50×100 的网格进行模拟(下同)。图7 为双侧计算模型模拟的飞片自由面(f=0.81)。由图7 可知,双侧计算模型模拟的飞片自由面速度和实验测量的飞片速度一致。图8 为飞片与阴极之间的真空间隙 g (t) 、飞片和阴极电流加载端厚度方向上烧蚀宽度之和 gm(t) 的比较。由图5、8 可知,单、双侧计算模型模拟的飞片与阴极之间的真空间隙 g (t) 和飞片与阴极烧蚀宽度之和gm(t) 是不同的,双侧计算模型模拟的g (t) 、gm(t) 更大。图9 为双侧计算模型模拟的飞片和阴极烧蚀宽度。由图9 可知,尽管飞片和阴极的加载电流相同,但是飞片和阴极板的烧蚀宽度度是不同的,飞片的烧蚀宽度大于阴极板的烧蚀宽度。飞片和阴极的烧蚀宽度不同,是由飞片和阴极板的厚度不同造成的。只有当飞片和阴极的厚度相同时,飞片和阴极的烧蚀宽度才一致。图10 为双侧计算模型模拟的飞片、阴极的电流加载面的位移。由图10 可知,飞片电流加载面的位移随时间持续增大,阴极电流加载面的位移不随时间持续增大,在磁驱动实验中后期,阴极电流加载面基本保持不动,约为1 mm。在实验结束时,飞片烧蚀宽度对边界磁场强度的影响为21.9%,阴极烧蚀宽度对边界磁场强度的影响仅为4.8%。因此,PTS-064 磁驱动单侧飞片实验能采用单侧计算模型模拟的原因,不是阴极板面保持位置不动,而是阴极电流加载面的位移不随时间持续增加,在磁驱动实验后期保持基本不变,且位移较小。
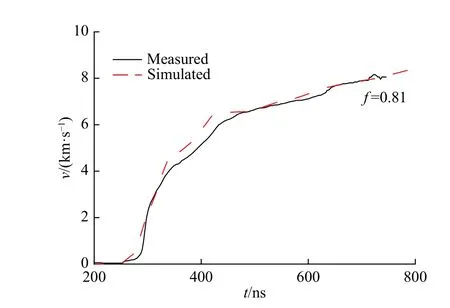
图 7 PTS-064 实验飞片自由面速度的双侧计算结果Fig. 7 Flyer plate free-surface velocities of experiment PTS-064 simulated by two-sided computational model

图 8 PTS-064 实验真空间隙和飞片烧蚀宽度的双侧计算结果Fig. 8 Vacuum gap and flyer plate ablation depth of experiment PTS-064 simulated by two-sided computational model
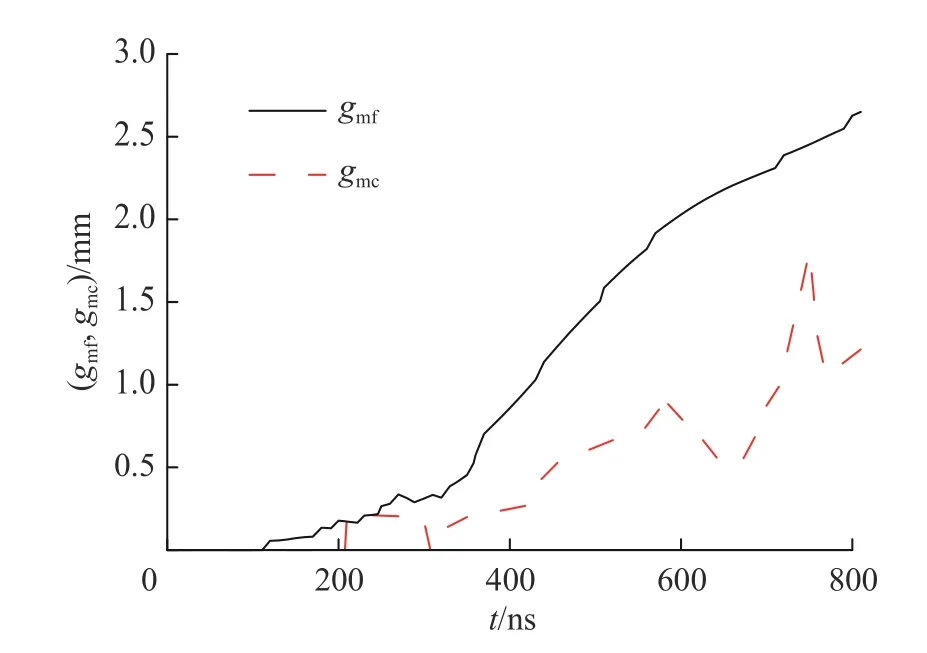
图 9 PTS-064 实验飞片和阴极烧蚀厚度的双侧计算结果Fig. 9 Flyer plate and cathode ablation depths of experiment PTS-064 simulated by two-sided computational model

图 10 PTS-064 实验飞片和阴极电流加载面位移的双侧计算结果Fig. 10 Displacements of flyer plate and cathode current-loading surfaces of experiment PTS-064 simulated by two-sided computational model
实际上,磁驱动单侧飞片实验也是一种双侧飞片实验,因此磁驱动单侧飞片实验的实际电流有效系数为双侧计算模型的电流有效系数。在PTS-064 磁驱动单侧飞片实验中,飞片实验的实际电流有效系数是0.81。采用单侧计算模型时,由于未考虑阴极的运动情况和烧蚀情况的影响,使用电流有效系数0.81 模拟PTS-064 实验时,计算的飞片边界磁场强度比实际磁场强度偏大,因此不能采用0.81 作为单侧计算模型的电流有效系数。由于阴极电流通过面对边界磁场强度的影响较小,仅有百分之几,因此可通过略微调小电流有效系数,使边界磁场强度与实际磁场强度基本一致,从而获得与实验测量一致的模拟结果。PTS-064 磁驱动单侧飞片实验中,单侧计算模型的电流有效系数为0.77,比实际电流有效系数小5%。
采用单侧、双侧计算模型对PTS-061 磁驱动单侧飞片发射实验进行了模拟。图11 为PTS-061 实验的测量电流。图12 为PTS-061 实验单、双侧计算模型模拟的飞片自由面速度。单侧计算模型使用的电流有效系数为0.795,双侧计算模型使用的电流有效系数为0.83。由图12 可知,单、双侧计算模型都能正确模拟PTS-061 磁驱动单侧飞片发射实验。图13 为PTS-061 实验双侧计算模型模拟的飞片、阴极的电流加载面的位移。与PTS-064 实验相同,在磁驱动飞片实验后期,飞片电流加载面的位移明显大于阴极电流加载面的位移;飞片电流加载面的位移增长较快,阴极电流加载面的位移增长较慢,趋于一个小的常数值。阴、阳极电流加载面之间距离的增加,主要是由飞片电流加载面的位移导致的。实验结束时,飞片电流加载面的位移为4.9 mm,阴极电流加载面的位移仅为1.7 mm;飞片烧蚀宽度对边界磁场强度的影响为20.7%,阴极烧蚀宽度对边界磁场强度的影响仅为7.2%。能采用单侧计算模型模拟PTS-061 磁驱动单侧飞片实验的原因是,磁驱动实验后期飞片电流加载面的位移远大于阴极电流加载面的位移。
在PTS-061 磁驱动单侧飞片实验中,实验的实际电流有效系数为0.83,单侧计算模型的电流有效系数为0.795,比实际电流有效系数小4%。

图 11 PTS-061 实验的电流Fig. 11 Current of experiment PTS-061
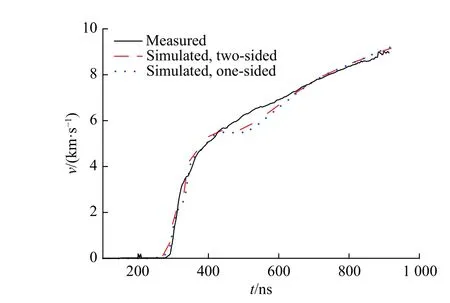
图 12 PTS-061 实验飞片自由面速度的单、双侧计算结果Fig. 12 Flyer plate free-surface velocities of experiment TS-061 simulated by one-sided and two-sided computational models

图 13 PTS-061 实验飞片和阴极电流加载面位移的双侧计算结果Fig. 13 Displacements of flyer plate and cathode current-loading surfaces of experiment PTS-061 simulated by two-sided computational model
4 结 论
为了正确理解磁驱动单侧飞片发射实验可采用单侧计算模型模拟的原因,建立了磁驱动单侧飞片发射实验的双侧计算模型。采用双侧计算模型对磁驱动单侧飞片发射实验进行了模拟分析。磁驱动单侧飞片发射实验可采用单侧计算模型不是因为阴极板面保持位置不动,而是阴极电流加载面的位移不随时间持续增加,在磁驱动实验后期保持基本不变,且位移较小。由于阴、阳极的厚度不同,磁驱动单侧飞片发射实验中阴、阳极的烧蚀宽度不同,薄的飞片烧蚀更快,烧蚀宽度更大。只有当阴、阳极板厚度相同时,阴、阳极的烧蚀厚度才一致。单侧计算模型模拟的电流有效系数总是小于双侧计算模型模拟的电流有效系数。这是因为,采用单侧计算模型时,未计算阴极电流加载面的位移,从而致使边界磁场强度比实际磁场强度偏大,因此单侧计算模型模拟使用的电流有效系数比双侧计算模型模拟的电流有效系数更小。阴极电流加载面的位移在实验后期不持续增大,保持在一个小的位移,它对边界磁场强度的影响约为百分之几,因此,单侧计算模型模拟使用的电流有效系数比双侧计算模型模拟的电流有效系数略小(约百分之几)。
