波浪中航行船体的非定常波数值模拟

王梓任 陈磊

摘    要：本文以三维移动脉动源格林函数为积分内核，根据线性势流理论，采用面元法求解体各运动模态振幅的辐射势及绕射势，利用伯努利方程求解船表面的波浪压力;通过压力积分获得船体所受波浪载荷;将所求得的各速度势代入自由面动力学条件求解船体周围的非定常波;以一修正的wigly模型为例，通过和模型试验结果的比较，验证了本文方法的可靠性。

关键词：船体; 非定常波; 势流理论; 三维移动脉动源

中图分类号：U661.32                            文献标识码：A

Abstract： A 3D frequency domain analysis solution based on the potential theory and the boundary theory is developed to investigate the unsteady waves for a ship advancing in regular waves. The 3D translating-pulsating source Green function is chosen to simulate the radiation and diffraction wave potentials. By using these potentials in the Bernoulli equation， hydrodynamic pressure is obtained， and wave loads of the ship are obtained from integrating the relative pressure over the mean wetted surface of the ship. By using the diffraction potential and radiation potential in the free surface hydrodynamic condition， radiation and diffraction waves are obtained. Validation is performed through studying hydrodynamic terms， the predictions obtained by the present method show general agreement with the experiments.

Key words： Hull; Unsteady waves; Potential theory; 3D translating-pulsating source

1     引言

波浪中航行的船舶因入射波的作用会作摇荡运动，入射波与船体接触时会产生反射作用并向船外传播绕射波，入射波、辐射波及绕射波构成了船舶复杂的非定常波系。这种非定常波系无论是在理论研究还是在工程实际中都扮演着重要作用，常用来评估船体的耐波性能。比如：在采用波形分析法研究船体在波浪中的阻力增值时，就需要试验测量或者理论预报船体的这种非定常波系;又比如：舰船横向补给时，船体间的液面抬升則主要是由补给舰与接收舰产生的非定常场波系相互干扰和作用的结果，这种液面抬升会影响干货补给的安全。因此，理论研究中常常需要确定船船之间的这些复杂波系的性质，从而为补给参数的设计提供依据。

从定常波系的定义可知这种波浪是复杂的，理论预报时不仅要准确预报船体的摇荡运动来确定辐射波，同时还需要求解入射波遭遇船体时的反射波。通常，理论预报时入射波作为已知量，重点是预报船体的辐射波及绕射波。辐射波及绕射波的理论计算是非常复杂的，需考虑船体所受的波浪作用力、运动响应、航速U及摇荡频率ωe等的影响，这和求解静水中船体航行时产生的定常波系有本质的差异。

文献[1]采用等相分析法，研究了航行于波浪中的船体产生的非定常波系的模态组成及各模态波随船体航速及摇荡频率的变化规律，并指出船体的非定常波和斯特劳哈尔数τ （ τ = Uωe / g，g为重力加速度）密切相关：当0 < τ < 0.25时，非定常波中包含环形波、内侧楔形波及外侧楔形波三个模态;当 τ > 0.25时，非定常波中包含环形-扇形波、扇形波及内侧楔形波三个模态。

三维移动脉动源格林函数，严格满足有航速时的线性自由面条件[2]，是求解有航速时船体辐射及绕射波的一种有效工具[3]。但该函数表达式复杂，被积函数为奇异且具有高频振荡的复变函数，这给应用该函数来求解船体的非定常波带来了困难[4，5]。近年来，众多学者针对该函数的数值计算方法进行了研究[6，7，8]，获得了许多有效而又稳定的积分方法，从而为采用该格林函数求解船体的非定常波提供了基础。本文以该函数为基本内核，构建了波浪中航行船体非定常波的预报模型，通过模型试验验证了该方法的可靠性。

2     基本数学方程

2.1   速度势

2.2   边界元积分方程

满足上述边界条件的速度势φj（j=1～7），可用合适的点源形式的格林函数或混合使用点源和点偶形式的格林函数在物面上的分布来表达。其中，采用点源形式的格林函数来求解速度势的方法称为分布源法;采用混合形式的格林函数来求解速度势的方法称为直接速度势方法。本文采用分布源来表达速度势：

3    数值求解

3.1  水动力系数及波浪干扰力

船体第j模态运动在船体平均湿表面上诱导的辐射速度势为φj η j，将其代入线性伯努利方程并沿船体平均湿表面对压力幅值进行积分，然后向i方向投影，则可求得该模态辐射波在船体i方向产生的力矩的幅值f Rij为：

4    算例分析

非定常波形的计算涉及到辐射及绕射问题，并和船体的运动相关，因此要验证上述数学模型的可靠性，先要验证该模型求解船体水动力项及运动响应的精度。本文以一修正的Wigley为计算对象，针对其在规则波中运动时的辐射、绕射、运动响应问题先进行计算，并和已有的模型试验结果进行比较来考察该算法的可行性。

Wigley模型的主要参数如表1所示，模型的数学表达式参见文献[10]。

（1）进行辐射问题计算时，船模速度对应的傅汝德数fn=0.2;船体作摇荡运动时的无因次波数k0L的范围为1～40。

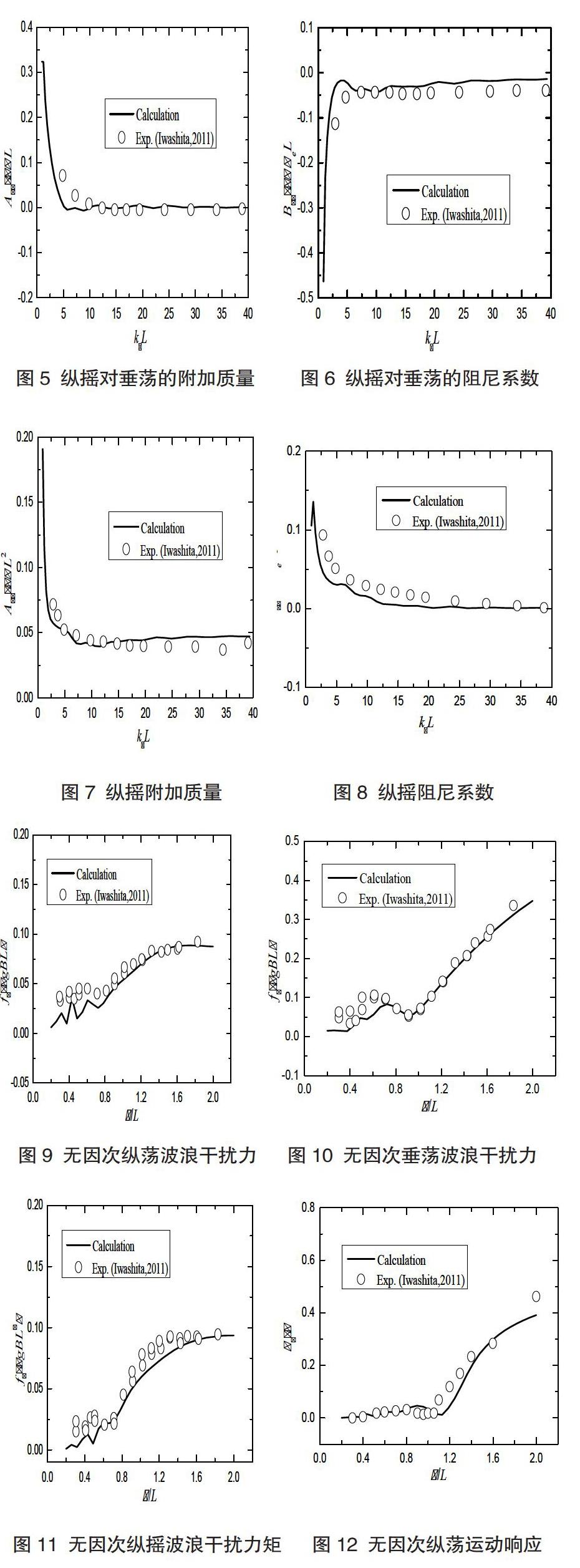
图1～图4分别为船模作垂荡运动时在垂荡方向及纵摇方向的水动力系数的计算结果;图5～8为船模作纵摇运动时在垂荡方向及纵摇方向的水动力系数的计算结果;图中还给出了文献[10]的模型试验结果。从上述图中可见：在整个频率计算范围内，计算所得水动力系数和模型试验的结果均吻合较好，从而验证了上述数学模型求解辐射问题的可靠性;另外，从上述图中还可见： 在0

（2）为验证数学模型求解绕射问题及船模在波浪中运动响应计算的可靠性，计算工况取船模在规则波中顶浪航行。

船模速度对应的傅汝德数fn=0.2，入射波为规则波，无因次波长范围λ/L为0.2～2。

由图9～11可以看出：计算结果与试验结果吻合良好，表明本文数学模型求解绕射问题的可靠性;图12～14给出了船模的纵荡、垂荡及纵摇运动响应的计算结果，图中还给出了文献[10]的模型试验结果。从上述图中可以看出：计算结果和预报结果也吻合良好。

（3）上述一系列计算，证明使用三维移动脉动源格林函数可以准确预报船体的波浪作用力及运动响应，从而证明了该函数预报航行船体辐射问题及绕射问题的可靠性。

以此为基础，仍采用修正的Wigley模型为对象，对其绕射波及辐射波进行计算，并和文献[10]的模型试验测量结果进行比较。

图15给出了自由面的计算域及网格的划分示意图，由于对称性，仅取了船模左舷一侧作为计算域。自由面的计算范围为 -5≤X/（L/2）≤2、0≤Y/（L/2）≤1.75的长方形区域，其中X、Y为随船坐标系所在的纵向和横向坐标。

图16、图17分别给出了当λ/L=0.5、fn=0.2时船模在规则波中顶浪航行情形下产生的绕射波波形的模型试验和计算结果。从图中可以看出，计算结果所在的区域和试验测量结果所在区域所得的波形吻合较好，表明直接采用三维移动脉动源格林函数来模拟船模的绕射波是可行的。

另外，从这些波形图可见，无论是辐射波还是绕射波，都被限制在一个半楔形区域内，在这些区域内传播波占主导，而在楔形区外基本无波浪传播，而且对比辐射波及绕射波可知辐射波的半楔角要大于绕射波所在楔形区的半楔角，这是因为算例中辐射问题对应的参数要大于绕射问题对应的参数。这和文献[2]所提船体波形的传播特性是相符的。

5    结论

本文建立了求解波浪中航行船体非定常兴波的数学计算模型，通过数值计算与模型试验的比较，验证了该数学模型的可靠性，并证明了采用三维移动脉动源格林函数来求解船体复杂的非定常波是可行的。因此，可引进该模型来求解船舶在波浪中阻力增值及航行补给舰船间的液面抬升等工程实际问题，这也是下一步需要开展的研究工作。

参考文献

[1] Noblesse， F. and Hendrix， D.， On the theory of potential flow about a ship       advancing in waves[J]. Journal of Ship Research， 1992.1 （ 36 ）： 17-29.

[2] 刘应中，缪国平.船舶在波浪中的运动理论[M]. 上海交通大学出版      社，1986， 90-102.

[3] Noblesse， F.， Velocity representation of free-surface flows and Fourier-Kochin      representation of waves[J]. Applied Ocean Research， 2001.23： 41-52，.

[4] Xu Y. and Dong W.C.， Study on Characteristics of 3-D Translating-pulsating      Source Green Function of Deep-water Havelock Form and its Fast Integration       Method [M]， China Ocean Engineering， 2011.3（25）： 365-380.

[5] Du， S. X.， Hudson， D. A.， Price， W. G.， et al.： Prediction of three-dimensional       seakeeping characteristics of fast hull forms： influence of the line integral terms      [J]. 25th International conference on fast sea transportation， Petersburg （Russia），        2005. 27-30.

[6] Inoue， Y.， Kamruzzaman， M.： Analysis of hydrodynamic characteristics for       arbitrary multihull ships advancing in waves[J]. Journal of Marine Science       and Technology， 2008.13（3）： 231-243.

[7] 許勇，董文才. Havelock型格林函数振荡项数值积分的稳定性研究[J].      计算力学学报，  2013. 30 （5）： 657-663.

[8] 洪亮，朱仁传，缪国平等. 三维频域有航速格林函数的数值计算与分     析[J]. 水动力学研究与进展，  2013. 28（4）： 423-430.

[9] 戴遗山，  段文洋.  船舶在波浪中运动的势流理论[M].  北京：  国防工      业出版社，  2008.

[10] Iwashita H.， Kashiwagi M.， Elangovan M.， etc. On an unsteady wave pattern        analysis of ships advancing in waves[J]. Journal of the Japan Society of        Naval Architects and Ocean Engineers. 2011. 6 （13）：  95-106.