基于初始种群对遗传算法的收敛性探讨

殷玲玲，苏剑锋

(六安职业技术学院，安徽 六安 237000)

0 引言

遗传算法通过对达尔文提出的自然选择与进化学说进行模拟，同时融合计算机算法最终完成可以全局统筹的概率搜索算法.这种算法能够在解决具体问题时首先圈定一个先大致潜在解的集合作为概率搜索算法的初始种群.潜在集合一般由计算机随机生成，数目统一且每一个个体代表不同的计算机编码，其中最优解即为初始生成的个体进化得到的，每一个不同的生物个体依据其不同的基因特征生成代码，以便于我们验证优胜劣汰的自然选择法则.在进化过程中需要保持种群的多样性使得算法更加精确、科学，同时其收敛性也相对更加准确，此时需要设定小概率的变异事件，使其更加贴近自然选择的范围.遗传算法的收敛性分析和收敛速度的研究一向是研究的重要方向.其中种群的初始分布是最先要考虑的问题.林阳等人(2017)提出运用多种群遗传算法的逆运算方式，同时引用适应度函数来提高函数的收敛速度[1].孙佳正等人(2018)提出统一种群中，依据缺陷这一要素将种群分为多个整体，通过交叉对比的方式提高算法搜索效率[2].薛愈洁等人(2018)提出利用遗传算法分类器实现系统匹配，通过仿真可以提高算法的精度[3].基于此，可以看出，遗传算法在解决高峰值和复杂的函数问题的时候，并不能保证收敛的速度和最终能收敛到最优解，从初始种群的选择这一角度，能够知道正确的初始种群构造标准.

1 初始种群模型模拟

1.1 初始种群收敛性模型

遗传算法收敛性模拟需要考虑包括种群规模、变异率在内很多的影响因素，这些因素均会对算法的收敛速度和概率产生不同的影响.初始种群对遗传算法的收敛性的影响，前所做的研究还不多.本次测试利用找到的随机初始种群的两种产生方法，对两者产生的初始种群(即随机数)进行统计和分析，并对其应用于遗传算法的效果进行了测试.这两种方法，一种是经典的系统自带的随机数发生函数，还有一种是自定义的随机数产生函数.

以下三个测试函数都是要求它们的最大值：

1)f(x)=xsin( 10pix)+ 2.0x=[-1.0,2.0] 最大值为3.850 274

2)f(x)=100*(x1*x1-x2)*(x1*x1-x2)+(1-x1)*(1-x1) -2.048<=xi<=2.048最大值为3 905

1.2 遗传算法交叉率与初始种群关系确定

初始种群产生过后，需要不断多次地模拟进化过程，最终才能得出最优解的方案.在完成进化操作过程中，个体在交叉操作之后产生了新个体，这一新个体的出现实际上是在整体空间上完成有效搜索的过程.交叉概率太大时，初始种群中个体更新很快，会造成高适应度值的个体很快被破坏掉；概率太小时，交叉操作很少进行，从而会使搜索停滞不前，造成算法的不收敛.本次试验，就对交叉率和初始种群的关系进行了分析[4].求最大值：f(x)=100*(x1*x1-x2)*(x1*x1-x2)+(1-x1)*(1-x1)-2.048<=xi<=2.048最大值为 3 905.926.

1.3 种群规模与初始种群关系分析

种群规模是遗传算法的一个参数，在研究过程中并没有一定的依据，总是按照经验的习惯来选取.然而一些研究表明在对遗传算法计算的过程中需要考虑种群规模的影响，这是由于不同种群的遗传模式不同.为了保持算法的准确性，需要扩大种群采样点，从而提高算法性能，但是采样点也不宜过多，如果采样点过多则会增加计算量，减缓算法的收敛速度[5].因此，随机产生的初始种群，需要有一个合适的种群数目，来达到最有效的利用率.本次实验，选择了一个二维函数，利用不同的种群规模进行测试，期望找到种群规模和初始种群之间的关系.求最大值：f(x)=100*(x1*x1-x2)*(x1*x1-x2)+(1-x1)*(1-x1)-2.048<=xi<=2.048最大值为 3 905.926 227.

2 基于种群的遗传算法数据分析

2.1 初始种群对遗传算法收敛性数据模拟

两种随机数发生器产生的随机比较如图1所示.

图1 随机数发生器函数1的随机比较图

函数2的变量x1，x2在[-2.048,2.048]之间的分布如图2所示.

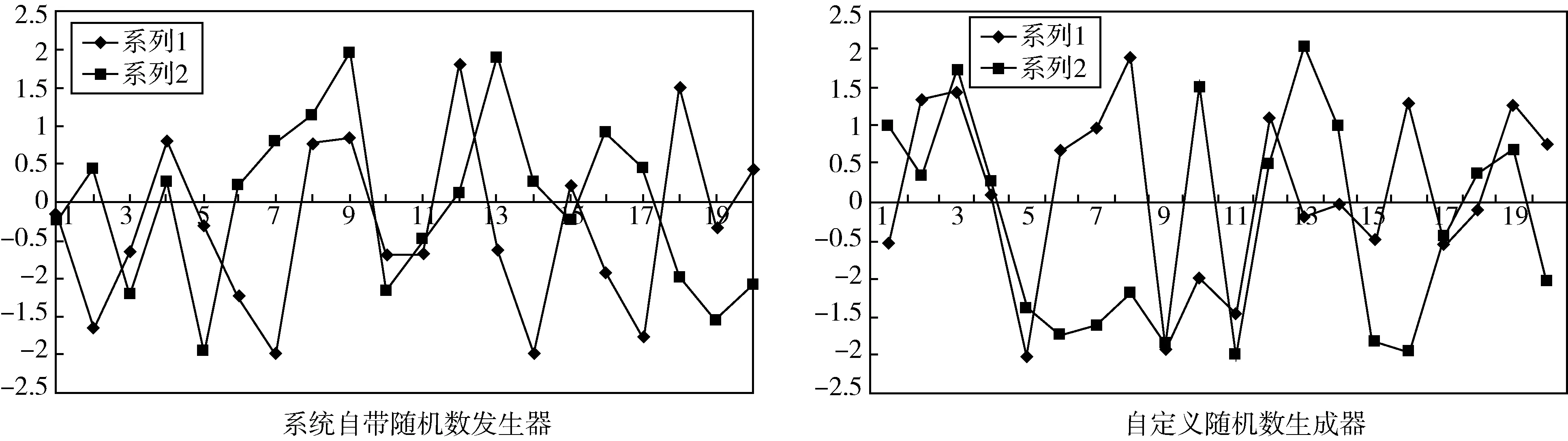
图2 随机数发生器函数2的随机比较图

由图2可知，系统自带的随机数发生器，产生的随机数，在[-2， -1]，[-1 ,0]，[0 ,1]，[1 ,2]之间的分布数目分别为11,11,13,5个，计算分布方差为6，而自定义的随机数发生器的结果为9，11，7，13，计算分布方差为3.33，点的分布更均匀.通过两种随机数生成器的比较，系统自带的随机数发生器所产生的随机数分布方差过大，可见数字的分布并不均匀，而自定的随机数发生器得到的随机数明显分布更加均匀.由上述两种随机初始种群产生法的应用中，我们可以看出，初始种群分布的均匀性、多样性，对遗传算法的收敛速度有促进作用.

2.2 遗传算法与初始种群交叉率分析

图3 遗传算法与初始种群交叉率分析图

本实验的进化参数设置如下：采用二进制编码，适应度函数取函数体本身.取种群大小为80，染色体长度为10(精度为6位小数)，初始交叉概率为0.6，变异概率为0.001，迭代100代，独立运行5次，取平均最大适应度.测试函数的实验结果如图3所示(图中的横坐标表示进化代数，纵坐标表示平均最大适应度).

我们对比图3，可知该函数进行遗传操作时，交叉率较小时，个体更新缓慢，使得搜索停滞不前，造成收敛缓慢；随着交叉概率的提高，搜索加快，个体更新较快，整体的适应度很快提高，使得算法更加平稳、较快地收敛于最优解.由于交叉率取值过大，算法在运行的过程中，个体更新过快，以至于把较优的个体也淘汰掉，造成了算法早收敛于次优解.由上述实验结果可知，遗传算法随机产生初始种群，交叉概率太小会使得算法的不收敛.交叉概率的提高增加了遗传算法稳定、收敛于最优解的可能性.不过，交叉概率太大会造成收敛到次优解.由此可见，随机产生的初始种群，在进化过程中，需要选取合适的交叉率，一般来说是0.6～0.75左右，才能提高算法的收敛性.

2.3 种群规模与初始种群关系分析

种群规模与初始种群的关系函数实验结果：如图4所示.

图4 种群规模与初始种群的关系函数图

本实验分别选取了种群数为80，160，320，640，由图4可知，遗传操作该函数时，随着种群数目的增加，算法的收敛逐步接近于最优解，收敛速度也提高.不过在试验的过程中发现，种群数目增加了，算法的运算速度也变得缓慢，消耗的资源也变大了.由上述可知，对于这个二维函数，种群规模的扩大增加了其收敛于最优解的可能性.随机产生的初始种群，有一个较大的种群规模，无疑会增加算法的收敛速度和收敛质量.不过，种群规模较大，尽管可以增加优化信息，阻止早收敛的发生，但是无疑会增加计算量，因此确定初始种群的大小需要根据实际情况，做适当的调整.

3 结论

通过对种群规模、初始种群与遗传算法的收敛性的关系进行对比实验，从中得出一些规律，为遗传算法今后的应用提供帮助.同时，为初始种群方面来改进遗传算法的收敛性奠定了基础.

通过研究初始种群对遗传算法收敛性影响，我们得出以下结论：初始种群的均匀分布和多样性，对于提高算法收敛速度和概率，有很大帮助.种群分布越均匀，就越有可能找到最优解，使得算法更快地得到收敛.种群规模的确定，需要根据实际应用的情况来决定.交叉概率太小，交叉操作很少进行，从而会使搜索停滞不前，造成算法的不收敛；交叉概率太大，种群中个体更新很快，会造成高适应度值的个体很快被破坏掉，造成收敛到次优解.为了有利于初始种群的进化，有利于算法的收敛性的提高，我们需要选择合适的交叉率.