多变量广义系统的能观规范型

王永超,翟昌海

(吉林师范大学 数学学院,吉林 长春 130000)

0 引言

所谓能观规范型，就是能观系统的标准形状态空间描述，一个正常系统总可以化为能观规范型，而且能观规范型在系统的极点配置等综合问题中有着重要的应用[1].文献[2-6]研究了单输入单输出系统的问题，以及能控规范型和能观规范型问题，但没有考虑多变量广义系统的能观规范型问题，本文对其进行了补充.

1 预备知识

对于正则的广义系统

(1)

其中,x(t)∈Rn,u(t)∈Rm和y(t)∈Rl分别为状态、输入和输出向量;E,A∈Rn×n,B∈Rn×m,C∈Rl×n为定常矩阵;E为奇异矩阵,且假定degdet(sE-A)=r[7].

首先系统(A,B)能观的充要条件

rank[c1…cm/c1A…cmA/…/c1An-1…cmAn-1]=n

(2)

其中,C=[c1/c2/…/cm] .因此,在此式中存在n个线性无关的行.即任何能观的正常系统均相似于能观规范型.下面用一种特殊的情况来表示上述结构

(3)

其中*表示允许的非0值,空白处为0.

2 主要结果

定理1广义系统(1)能观的充要条件是[sE-A/C]在受限等价变换下具有形式

(4)

其中

则称式(4)为多变量广义系统(1)的广义能观规范型.

证明 必要性.由rank(E)=q,存在非奇异矩阵P和Q使

其中

C(n-q)m=(cij) ，i=1,2,…,(n-q);j=1,2,…,m

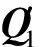
重复上述过程,有

或

其中

于是

(5)

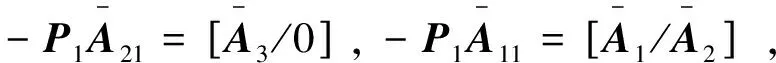
(6)

由于rank[sE-A/C]=n,因此

充分性.由受限等价变换不改变广义系统的能观性知,结论成立.

3 结论

综上可见,研究了多变量广义系统的能观规范型问题,但是多输入多输出的广义系统的能观规范型不唯一,这就导致了多变量广义系统的能观规范型形式的多样性.这里只介绍一种广义能观规范型.