基于EEMD-BP 方法的城市轨道交通进站客流短期预测

2020-03-31傅晨琳沙志仁

铁道运输与经济 2020年3期

傅晨琳，黄敏，沙志仁

（1.中山大学智能交通系统重点实验室，广东广州 510006；2. 广东方纬科技有限公司研发中心，广东广州 510006)

0 引言

城市轨道交通以其大运量、低成本和高环保的特点，逐渐成为发展智慧交通的关键。城市轨道交通站点客流量是评价其服务水平和实现城市轨道交通资源有效配置的基础数据和依据，因而掌握客流波动的特征和规律，可以实现科学合理地预测各站点短期客流对开展客流控制和列车调度。由于城市轨道交通进站客流受到站点位置、节假日、重大事件等因素的影响，客流序列的波动呈现很强的非线性和非平稳性，客流量的预测难度较大。

客流预测常用方法主要有ARIMA 时间序列模型、回归模型、神经网络等，郝勇等[1]运用时间序列模型通过客流7 d 均量分别进行系统日客流量的迭代预测和递推预测；李丽辉、Smith 等[2-3]分别采用随机森林回归和季节差分自回归移动平均模型预测短期交通量；李春晓等[4]提出一种基于广义动态模糊神经网络(GD—FNN)用于预测短时进站客流量。为更有效地利用模型的优点，互相弥补缺陷，组合预测的理论和方法已成为目前的趋势。王兴川等[5]构建基于小波分解与重构的GM—ARIMA客流预测模型，基于AFC 客流数据实现对大型活动期间的轨道交通客流预测；Yu 等[6]将经验模态分解法和BP 神经网络组合对地铁客流进行预测。

目前，有关城市轨道交通分时客流预测的研究较少，而且由于城市轨道交通进站客流在时空分布不均匀，呈现出非线性、非稳态的特点，传统的预测方法难以捕捉数据间的非线性波动，而时间序列存在间歇性，在数据分解时容易出现模态混叠的现象。为提高进站客流预测精准度，将噪声辅助数据分析的集合经验模态分解法和适合时间序列预测的BP 神经网络构建组合预测模型对城市轨道交通进站客流进行短期预测。

1 基于EEMD-BP方法的城市轨道交通进站客流短期预测模型

1.1 集合经验模态分解法

经验模态分解法(Empirical Mode Decomposition，EMD)是Huang 等人于1998 年提出的一种自适应信号时频处理方法[7]，特别适用于非线性非平稳信号的分析处理。由于自身优势和适用性，其在交通领域的应用日益成熟。而集合经验模态分解法(Ensemble Empirical Mode Decomposition，EEMD)是针对传统EMD 在处理间歇性的时间序列信号时会出现模式混合的情况而提出的改进算法[8]，利用EMD 尺度分离原则和噪声统计特性，在处理非平稳、非线性间歇性时间序列能有效抑制模态混叠，充分保持原有序列的动态性，区分异常状态，将信号逐级分解成不同频率和特征尺度的若干个独立的特征模态函数(Intrinsic Mode Function，IMF)。

EEMD 的分解原理是通过添加白噪声辅助分析，促进数据在分解中进行抗混处理，以抑制模式混叠现象。EEMD 的理论依据是在待分解信号添加白噪声，使其成为真实时间序列和白噪声的混合，利用白噪声频谱在整个时频的均匀分布特性使数据按照时间尺度自动分布到适合的参考尺度范围。由于白噪声具有零均值性，虽然每次分解中白噪声互不相同，经过多次分解求平均值后，噪声就可以互相抵消，信号本身才是唯一持久稳固的部分，即本质是一种添加白噪声的多次经验模态分解[9]，分解后的IMF 分量应满足近似为周期函数，且任意数据点的极值包络线的平均值为零。EEMD的分解流程图如图1 所示。

EEMD 分解的具体步骤如下。

（1）向原始序列X(t)中分别添加N次均值为0，幅值标准差为0.2 的白噪声，添加噪声后的序列为X’(t)，确定X’(t)所有的极大值和极小值。

（2）利用三次样条插值法分别拟合极大值和极小值的上下包络线，根据上下包络线计算其局部均值m(t)及差值d(t)，判断d(t)是否满足IMF 条件：如果满足，将d(t)表示为第i个 IMF 分量，并以剩余量r来替代X’(t)；第i个 IMF 分量通常被记作cn(t)；若不满足，则用X’(t)替代d(t)。

（3）重复以上步骤，当r为单调函数或小于某固定值时，一次分解过程完成，分解后的原始序列可表示成n个IMF 分量与剩余量r的和。

（4）将以上步骤多次分解对应的IMF 总体求平均值，消除白噪声的影响，得到EEMD 分解后的IMF 分量及剩余量，可表示为

图1 EEMD 的分解流程图Fig.1 Decomposition flow chart of EEMD

式中：cj(t)为第j个IMF 分量：r(t)为剩余量。

1.2 BP神经网络

BP 神经网络(Back Propagation Network)也被称为误差反向传播神经网络，是一种按照误差逆向传播算法训练的多层前馈神经网络，具有监督的学习模式，是目前应用最广泛的神经网络。BP 神经网络算法的基本思想是梯度下降法，通过反向传播不断调整网络的权值和阈值，使网络的实际输出和期望输出的误差平方和为最小。BP 神经网络模型结构通常包括输入层、隐含层和输出层，输入层负责接收神经网络的输入信息，隐含层位于中间，是输入层和输出层中神经元连接信息的传输带，并对输入信息进行分析处理，隐含层可以是多层的，输出层是将分析处理后的结果集合输出，即神经网络的输出。每一层都由不同数量的神经元组成，典型的单隐含层BP 神经网络的模型拓扑图如图2所示。

建立BP 神经网络模型需要确定包括隐含层层数、各层节点数、学习速率、迭代次数、各层神经元激励函数等因素，对网络性能有一定的影响，在应用时需要通过试验不断调整得出适应值。

1.3 EEMD-BP组合预测模型

为更准确地进行客流预测，将EEMD和BP 神经网络组合构建EEMD—BP 组合模型预测城市轨道交通短期进站客流，其组合思路为：先运用EEMD 对城市轨道交通日进站客流序列进行模态分解，再对分解后得到的IMF 分量进行识别和筛选，按照与原始时间序列的相关程度将分量分为高相关分量和低相关分量；接着设计实验研究不同分量组合形式输入BP 神经网络的客流预测情况，并对比分析各实验组的预测结果。简言之，组合模型分为数据分解阶段、分量识别阶段、客流预测阶段、结果分析阶段。

（1）数据分解阶段。由于城市轨道

交通客流数据是非线性、非稳态的，且具有间歇性，因而需要先通过EEMD 将原始客流序列分解为若干个简单独立的IMF 分量，分解出的IMF 分量按照频率由高到低排列，各自表示原始客流数据的局部特点，如振荡范围、变化趋势、周期模式等。分解本质是将影响原始序列波动的各成分特征分类分离出来，即原始客流序列呈现出的波动性就是这些分量叠加的结果。

图2 典型的单隐含层BP 神经网络的模型拓扑图Fig.2 Model topology diagram of BP neural network

（2）分量识别阶段。通过EEMD 分解后，将得到的IMF 分量中识别筛选出对原始客流序列有显著影响的高相关分量。高频分量的周期较短，代表较短时间范围内客流的波动模式，低频分量的周期较长，代表较长时间范围内客流的变化模式，而剩余量代表原始数据整个时间范围的长期变化趋势。为更好地分析IMF 分量与原始客流序列之间的内在关系，识别有意义的分量，用以下统计量来分析。①平均周期：定义为快速傅里叶变换的最大振幅所对应的频率的倒数，代表各 IMF 分量的波动周期；②Pearson 相关系数：用于衡量数据间的线性相关关系，相关系数越大，表示相应的分量与原始客流序列间的线性程度越强；③Kendall 相关系数：用于衡量定序变量间的线性关系，相关系数越大，表示分量与原始序列在某时刻变化方向一致性越高；④方差占比：每个IMF 分量方差所占数据列总体方差的比重。根据各统计量的值分析出原始客流序列的高相关分量。

（3）客流预测阶段。通过对IMF 分量的识别筛选之后，为对比和验证不同模式的预测效果，利用BP 神经网络设计以下6 组实验。①直接将原始客流时间序列作为神经网络的输入；②将分解后的所有IMF 分量以单独的方式作为神经网络的输入；③将筛选后的高相关性分量以单独的方式作为神经网络的输入；④将筛选后的高相关性分量以组合的方式作为神经网络的输入；⑤将筛选后的高相关性分量以单独的方式，低相关性分量以组合的方式作为神经网络的输入；⑥将筛选后的高相关性分量以组合的方式，低相关性分量以组合的方式作为神经网络的输入。

（4）结果分析阶段。为了合理比对不同输入模式的预测效果，采用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE) 3 个指标进行判断分析。均方根误差能体现预测误差的离散分布程度，值越大表示误差分布越离散，越偏离平均值，预测效果越差；平均绝对误差是预测值与算术平均值误差绝对值的平均，可避免误差互相抵消，更直观反映实际误差的大小，值越小表示实际误差越小；平均绝对百分比误差是绝对百分比误差的平均值，可用于评价模型预测结果的好坏，值越大说明预测效果越差。均方根误差σ、平均绝对误差ρ、平均绝对百分比误差τ3 个指标可以表示为

式中：n为所预测的时间段个数；y(t)为原始数据值；为预测值。

2 实例分析

广州珠江新城站为广州地铁3 号线和5 号线的换乘站，位于广州天河中央商务区，是广州最繁忙的城市轨道交通站点之一。以江新城站为样本，选取2016 年10 月10 日至11 月30 日期间工作日的分时进站客流作为原始数据，采用EEMD—BP组合模型对该站进行短期客流预测。

2.1 分解数据

根据珠江新城地铁站的运营时间，以15 min为间隔共2 774 个数据，珠江新城站部分工作日日进站客流随时间的变化如图3 所示。由图3 可知，工作日客流在17 : 30—19 : 30 呈明显的晚高峰，对应工作客流下班通勤，也是站点实施常态化客流控制的时段。另外，客流在21 : 00—22 : 00 之间还有一个小晚高峰，对应夜间活动返程客流。需要注意的是，由于灯光节的影响，少部分日期的22 : 00 附近出现客流异常情况。运用EEMD 对原始客流进行分解，采样期间工作日的进站客流序列分解为10 个IMF 分量和1 个剩余量，原时间序列及分解后得到的IMF 分量如图4 所示。将分解所得的IMF 分量按照频率由高到低依次排列，各自的波动代表了原始时间序列的波动特征成分，最后无法分解的部分为剩余量，剩余量单调递增，说明整个采样期间工作日的进站客流呈上升的趋势。

2.2 筛选高相关分量

为识别与原始序列相关程度较高的分量，对各分量进行平均周期、Pearson 相关系数、Kendall相关系数、方差占比4 个指标的统计分析，各IMF 分量的统计分析结果如表1 所示。从周期上看，IMF1 至IMF4 都体现了进站客流的分时波动，其中IMF2 和IMF3 对应了一天之内的2 个高峰，IMF4 体现了半天的波动性，恰好在时间上将白天平峰与晚间高峰分隔开，而IMF5 的波形与原始波形最为相似，体现了原始客流的日波动性；而IMF7 的周期接近5，体现了一周工作日的波动性；IMF10 的周期与原始客流时间范围一致，则体现整个采样时间的客流变化特征。从Pearson 相关系数和Kendall 相关系数看，IMF2 和IMF3 的周期虽然相同，但IMF3 的相关系数更大，说明IMF3 与原始序列的线性关系和一致性更高，因而IMF3 对应的是傍晚的高峰。总体来看，IMF2 至IMF5 的相关系数与其他分量相比明显更大，说明这些分量与原始序列的波动一致性较高，且他们的方差占比总和为全部占比的97.8%，说明他们是原始序列变化趋势中的主导分量。根据相关系数的参考准则[10]，选择分量IMF2 至IMF5 为高相关分量，其余分量为低相关分量。

图3 珠江新城站部分工作日日进站客流随时间的变化Fig.3 Daily passenger flow in the Zhujiang New Town Station

图4 原时间序列及分解后得到的IMF 分量Fig.4 Original time series and IMFs obtained after decomposition

2.3 客流预测

选用单隐含层结构神经网络建立预测模型。为提高预测精度，预测前对数据进行异常值剔除，剔除原始序列中受灯光节影响导致客流异常的3 d，将原数据分为训练集和测试集，其中训练集为前32 d 的数据，按8:2 划分训练集和验证集，最后3 d 为测试集。将每天的时间序列样本划分为4 个时段，分别是(06 : 00，12 : 00]，(12 : 00，17 : 00]，(17 : 00，20 : 00]，(22 : 00，23 : 45]。训练过程中，样本以15 min 为间隔，以6 为滚动单位，即取前6 个连续样本为基础训练预测下一个样本(以6 : 00—7 : 30 为输入预测7 : 45 数据，再以6 : 15—7 : 45为输入预测8 : 00的数据)。参数设置经过尝试，隐藏层激活函数为elu，输出层激活函数为linear，损失函数采用mae。按照实验方案的设计，输入节点个数基于滚动单位，IMF 分量及每日划分时段，隐含层节点数选择误差最小的最优数，各组实验的BP 神经网络训练的关键参数如表2 所示。

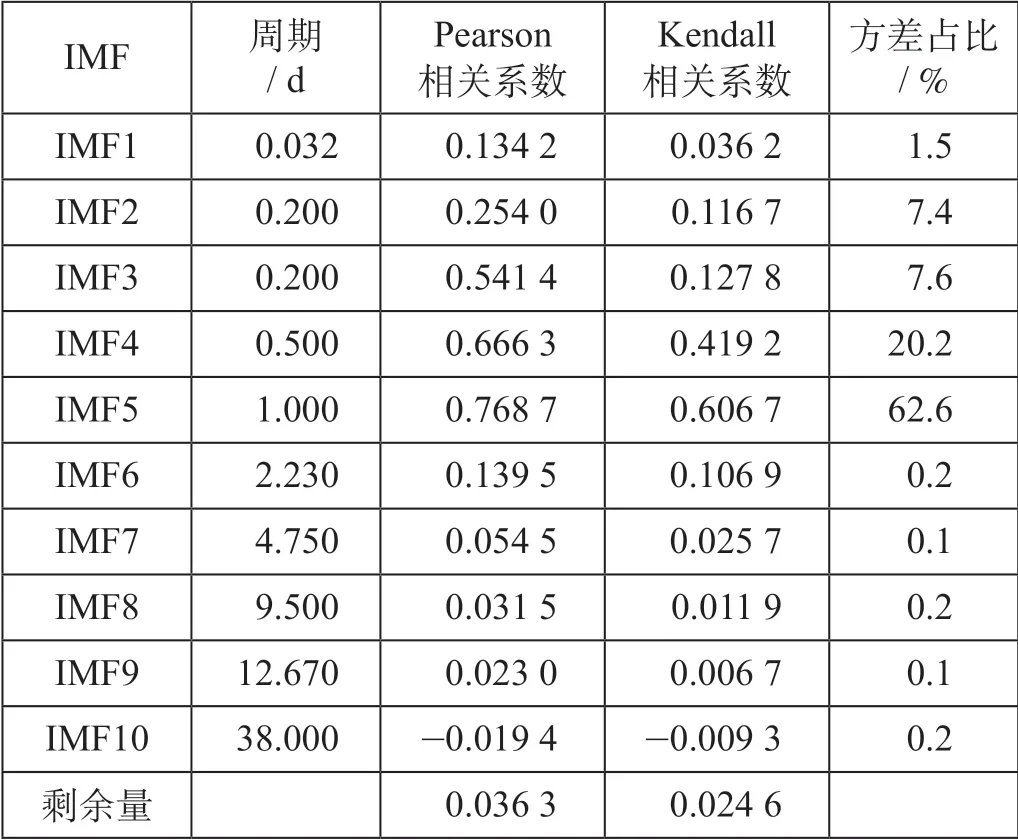
表1 各IMF 分量的统计分析结果Fab.1 Statistical analysis results of each IMF

表2 各组实验的BP 神经网络训练的关键参数Fab.2 Parameters of BP neural network in each group of experiments

2.4 预测结果分析

采用均方根误差、平均绝对误差、平均绝对百分比误差作为指标对EEMD—BP 组合预测模型的预测结果进行评价，各实验方案的预测结果评价分析如表3 所示。

通过表3 可以得出，将原始序列分解为特征分量的形式输入比直接将原始客流序列作为神经网络输入的预测效果精度高，高相关分量是预测精准度提高的关键特征分量，分量以组合的形式输入改善预测精度的效果更好，且将高相关分量和低相关分量分开作为输入得出最佳预测结果为实验6。实际数据与实验6 预测结果比较如表4 所示。