热离子能量转换器扩散工况的电流饱和特性
2020-03-30钟武烨郑剑平杨启法
钟武烨,吕 征,郑剑平,杨启法
(中国原子能科学研究院 反应堆工程技术研究部,北京 102413)
热离子反应堆电源具有比功率高、结构紧凑、寿命长等优点,俄罗斯(前苏联)TOPAZ型反应堆电源已经过空间飞行验证[1],是深空探测、空间基地等理想电源之一[2-3]。热电转换元件是堆电源的核心器件,热离子能量转换器通过热离子发射的方式实现热电的直接转换。运行过程中,核裂变加热发射极产生热电子发射,电极间隙充入的铯蒸气电离为等离子体,电子输运通过等离子体区域后到达接收极形成回路,工作参数或负载的变化均可使热离子转换器工作在电弧工况或扩散工况[4]。对电弧工况的热电转换特性进行了研究[5],对于电功率输出较小的扩散工况,虽仅存在于热离子发电元件电极的低温端(温度场边界效应导致),但该工况下伏安曲线的极限值(饱和电流、开路电压等)与热电转换过程的特征参量(发射极温度、吸铯功函数等)有关联而常被用作诊断分析[6]。因此,无论诊断分析还是电特性设计均需进行扩散工况的研究。
扩散工况的研究中,电流的饱和特性(即饱和电流的存在性及其机理)是最为集中的关注点。在诊断技术中,饱和电流是间接表征吸铯功函数的参量,而饱和电流的存在意味着扼流的产生,不利于功率的提升。目前,关于扩散工况饱和电流的研究已有较多的工作,包括基于量纲分析简化进行饱和电流的近似计算以及结合诊断的测量[7]。但仍有基础问题有待进一步深入,如饱和电流产生的条件与机理,电流逐渐增大至饱和的过程中,电极间隙电子势能分布等均有待细致描述。区别于文献的近似表达式,本文基于动理学方法建立扩散工况下电极间隙的等离子体输运模型,描述电流缓慢增大过程的伏安特性及电子势能分布,从而直观深入分析饱和电流的存在性及其机理。
1 扩散工况的等离子体输运的建模
热离子能量转换器电极间的等离子体在与电极接触的极窄区域(其尺度与德拜长度相当,远小于电极间隙)将形成等离子体鞘层,区别于准中性的等离子体。通常对热离子能量转换器电极间等离子体的描述分成3个区域:发射极鞘层、中间准中性等离子体区、接收极鞘层[8]。
对于中间准中性等离子体区需建立等离子体输运方程。现有扩散工况的研究中采用量纲分析手段将某些力场对输运的贡献忽略(如温度场的贡献),从而简化为带电粒子的扩散问题[9],这将限制方程的适用范围。根据现有的实验分析,扩散工况与电弧工况在输运本质上并无差别,其主要差别在于扩散工况下铯电离的机制主要是发射极表面热电离(通过边界条件描述),而电弧工况下主要是体电离的贡献[10]。本文在原电弧工况的输运模型[5]的基础上,忽略体电离项从而建立扩散工况的输运模型。
对于等离子体鞘层,则需处理为输运的边界条件,其包括发射通量与从等离子体返回通量,及其受等离子体鞘层的电子势能分布的影响。由于扩散工况下鞘层的电子势能分布与电弧工况下的有很大差异,因此以下对扩散工况的边界条件进行详细的讨论,电子势能跃变均以从发射极到接收极的方向为参照。
1.1 发射极鞘层的边界条件
热平衡态下,等离子体鞘层的热发射通量与从等离子体返回到发射极的通量达到平衡,此时处于零输出状态。发射极鞘层的电子势能分布由发射极鞘层上的电子浓度与离子浓度的相对大小决定,通常引入离子裕度β来描述热发射中和状态[11]。
(1)
(2)
(3)
其中:jes为饱和电子发射电流密度,由理查森方程描述;jis为饱和离子发射电流密度,由沙哈方程描述[8];mi、me分别为离子、电子质量;k为玻尔兹曼常数;TE、TCs为发射极、铯原子温度;e为电子电量;pCs为铯蒸气压强;Eion为铯的第一电离能;φE为发射极功函数。当β=1时,热发射的电子和离子恰好能相互中和,其鞘层电子势能分布如图1b所示,实际中出现的可能性极低;当β<1时,电子发射过剩,为使等离子体区域保持电中性,发射极鞘层的电子势能分布向上跃变,对电子形成了进入等离子体区域的势垒VTE(图1a);当β>1时,离子发射过剩,为使等离子体区域保持电中性,则其分布向下跃变VTE,从而促进电子进入等离子体区域(图1c)。
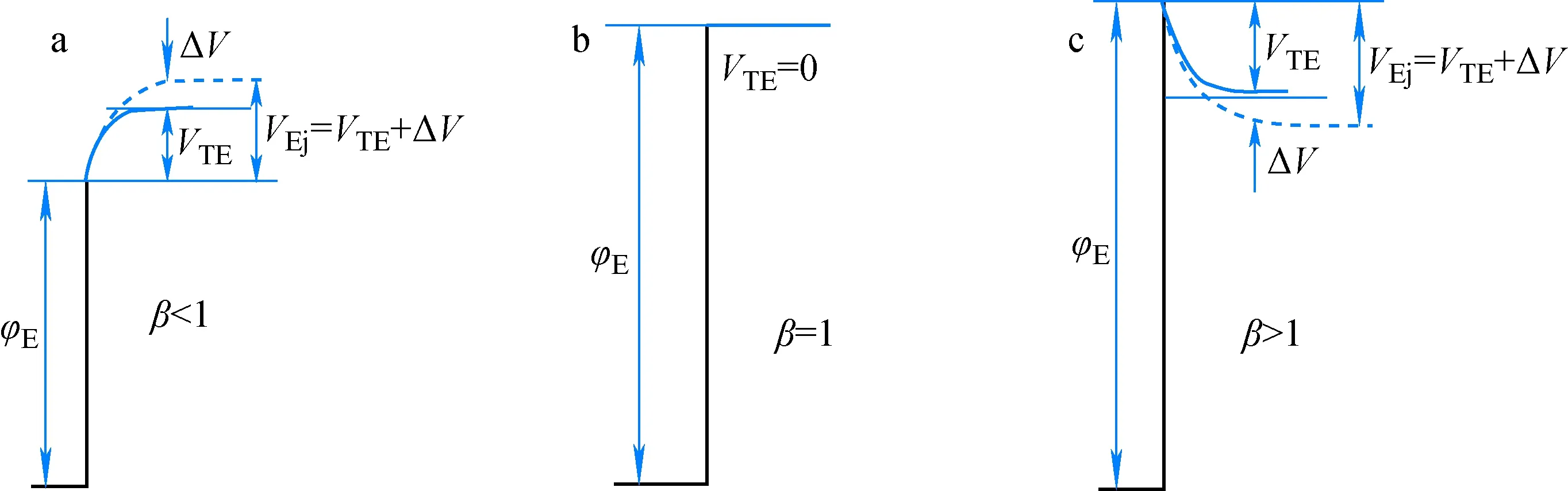
图1 发射极鞘层电子势能的分布Fig.1 Distribution of electron potential energy at emitter sheath
当热离子转换器工作在扩散工况时产生了电流输出,则热平衡态不能维持,但由于热发射电流较小,发射极边界条件可从热平衡态的鞘层特征扩展获得[9],实际的鞘层电子势能分布相对于热平衡态产生附加电势跃变ΔV,因此总跃变为VEj=VTE+ΔV,如图1虚线所示。
当离子裕度β<1时,鞘层电子势能分布如图1a所示,得到如下边界条件:
(4)
(5)
(6)

当离子裕度β>1时,鞘层电子势能分布如图1c所示,得到发射极鞘层与等离子体交界面上的通量边界条件:
(7)
(8)
(9)
1.2 接收极鞘层的边界条件
由于接收极温度仅有550 ℃左右的低温,热发射通量低,其边界条件主要受等离子体鞘层参量的影响,因此需根据具体工作点自适应地选择其跃变的方向。结合发射极鞘层的分析,扩散工况下电子势能可能的分布状态如图2所示,其中接收极鞘层的跃变包括向上跃变和向下跃变。
当输出电流较小时,接收极鞘层的电子势能需产生向上的跃变以形成对来自等离子体电子流的势垒,即VCj1>0,此时的边界条件为:
(10)
(11)
(12)
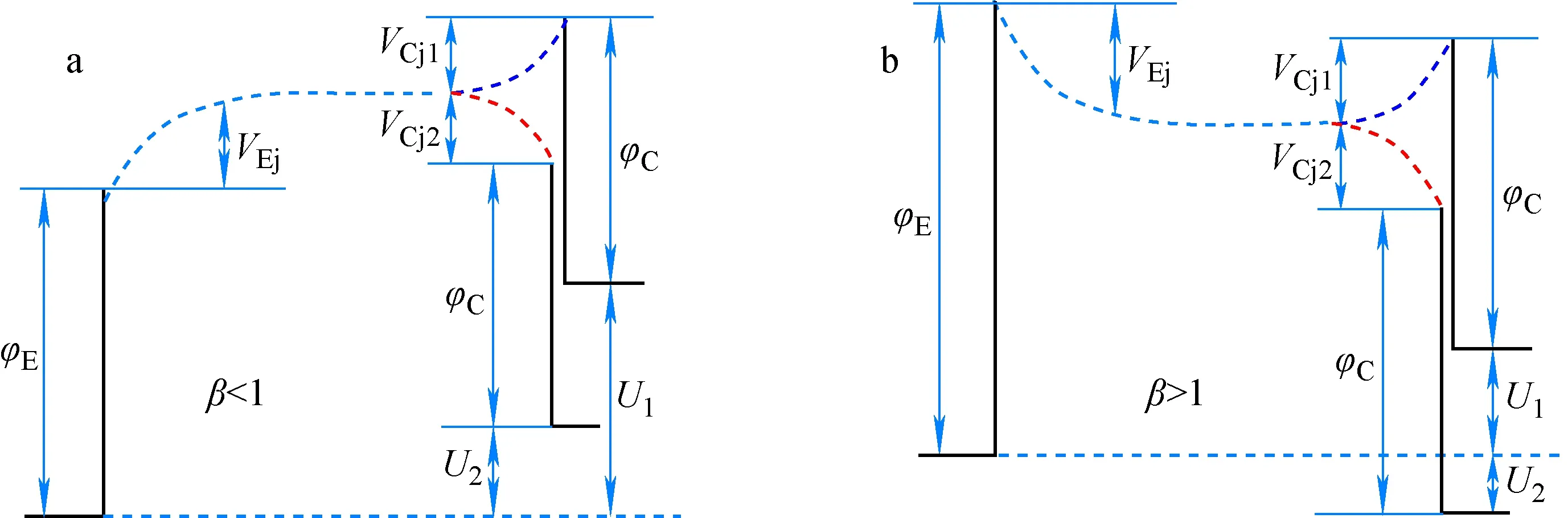
图2 热离子能量转换器扩散工况的电子势能分布Fig.2 Distribution of electron potential energy for thermionic energy converter operating on diffusion mode
当输出电流较大时,接收极鞘层的电子势能需产生向下的跃变促进来自等离子体的电子流,即VCj2<0,此时的边界条件为:
(13)
(14)
(15)
式中物理量符号的意义与发射极的情况一致。
2 模型求解与算法流程
根据上述建立的输运方程和采用的边界条件,两者具有很强的耦合关联,故本文建立的模型需数值求解,使得边界条件与输运方程自适应匹配。本文采用的算法流程如图3所示。
1) 输入计算所必要的参数:基本物理参量、热离子转换器的运行参数,包括电极温度(TE,TC)、铯温TCs、电极的吸铯功函数(φE,φC)、电极间隙d、总电流密度(输出电流密度)jtot等。
2) 给定接收极鞘层与准中性等离子体区交界处的电子温度TeC和接收极鞘层的电势跃变VCj作为迭代初始值,根据VCj的正负性选择相应的接收极边界条件模型,计算此边界的jeC、jiC、接收极等离子体浓度nC及电子能量流SeC。
3) 以计算得到的参量为边界值,采用龙格-库塔方法对输运微分方程进行积分,得到准中性等离子体区电子温度Te、等离子体浓度n、je、ji、负电势V、Se的分布,特别地,记发射极边界上的电子电流密度积分为je_inte(TeC,VCj)、离子电流密度积分为ji_inte(TeC,VCj)。
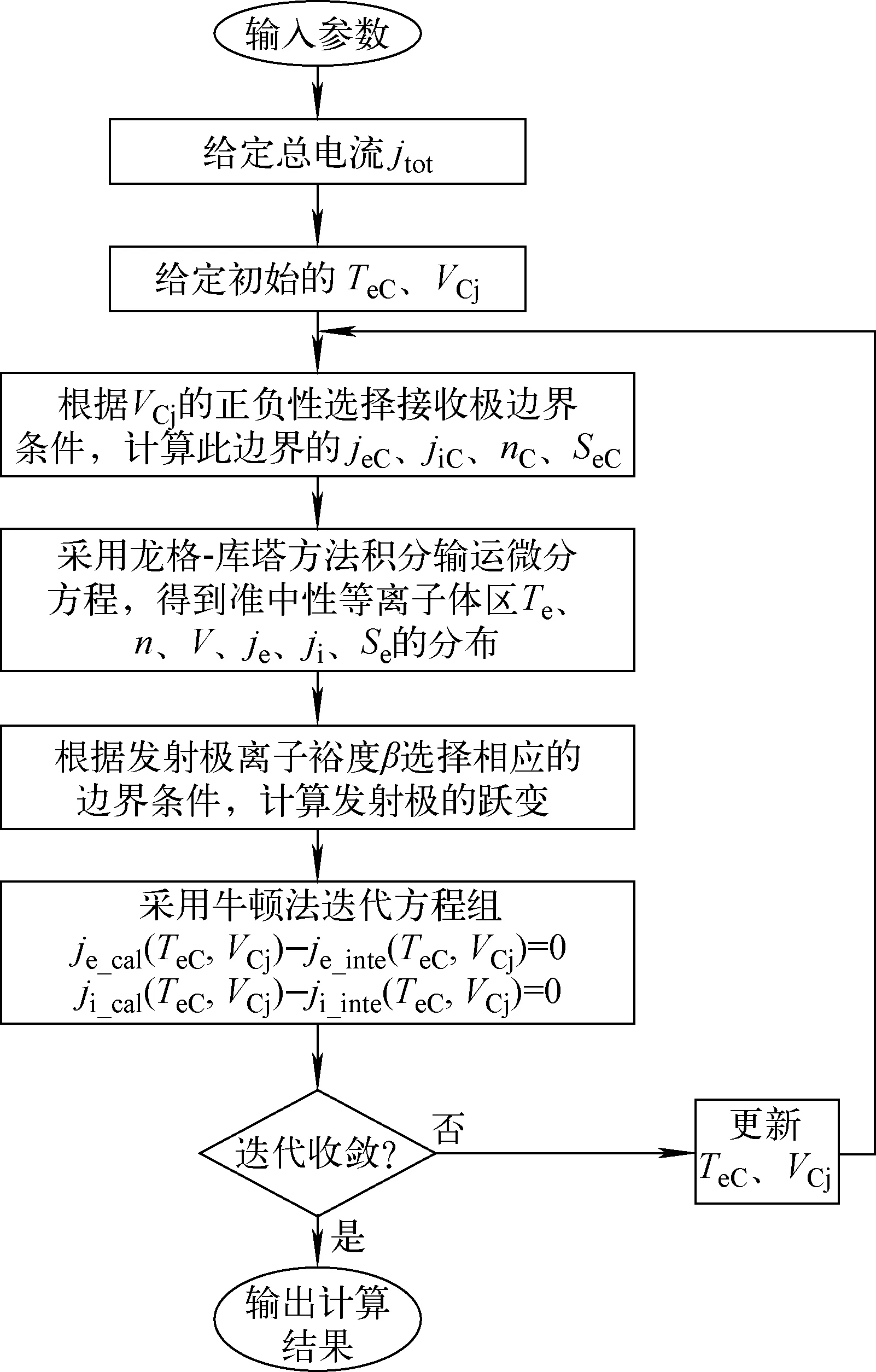
图3 热离子转换器扩散工况等离子体输运计算算法流程Fig.3 Algorithm flow of plasma transportation of thermionic energy converter operating on diffusion mode
4) 根据发射极离子裕度β选择相应的边界条件,计算发射极的电子势能跃变VEj及ΔVE,并计算相应条件下发射极边界上的电子电流密度je_cal(TeC,VCj)、离子电流密度ji_cal(TeC,VCj),并与积分所得边界值联立成方程组je_cal(TeC,VCj)-je_inte(TeC,VCj)=0与ji_cal(TeC,VCj)-ji_inte(TeC,VCj)=0。采用牛顿迭代法求解方程组,直至收敛到设定的精度。若发散,则重新选择初始条件进行计算。
5) 输出计算结果。
3 结果讨论
3.1 程序输入
根据上述建模过程,不同的离子裕度β将影响边界条件的选择,从而使模型得到不同的解(对应不同的输出状态)。发射极温度是改变离子裕度β的重要手段,为在较宽的β范围(覆盖其临界值1)内研究扩散工况下的电流饱和特性,本文通过改变发射极温度TE来改变β;同时,为与现有文献的测量值进行对比,本文在选定电极材料为Mo-Mo电极对的基础上,限定了若干组特定的输入参数,列于表1。本文程序的输入包含电极温度(TE,TC)、电极功函数(φE,φC)、铯温TCs(固定)、电极间隙d(固定)、输出电流密度jtot等7个参数。将上述工作参数作为程序的输入,获得计算结果。
3.2 输入的合理性判定
由程序的输入本身并不能判断热离子转换器具体的运行工况,因此需对输入进行扩散工况的合理性判定。依据模型的计算结果,等离子体的德拜长度远小于特征尺寸(电极间隙宽度),说明电极间隙形成了等离子体(图4a);且电离长度远大于电极间隙宽度,据此可进一步判定表1所示参数的热离子转换器工作在扩散工况(图4b)。

表1 程序计算中输入的工作参数Table 1 Input working parameters for procedure
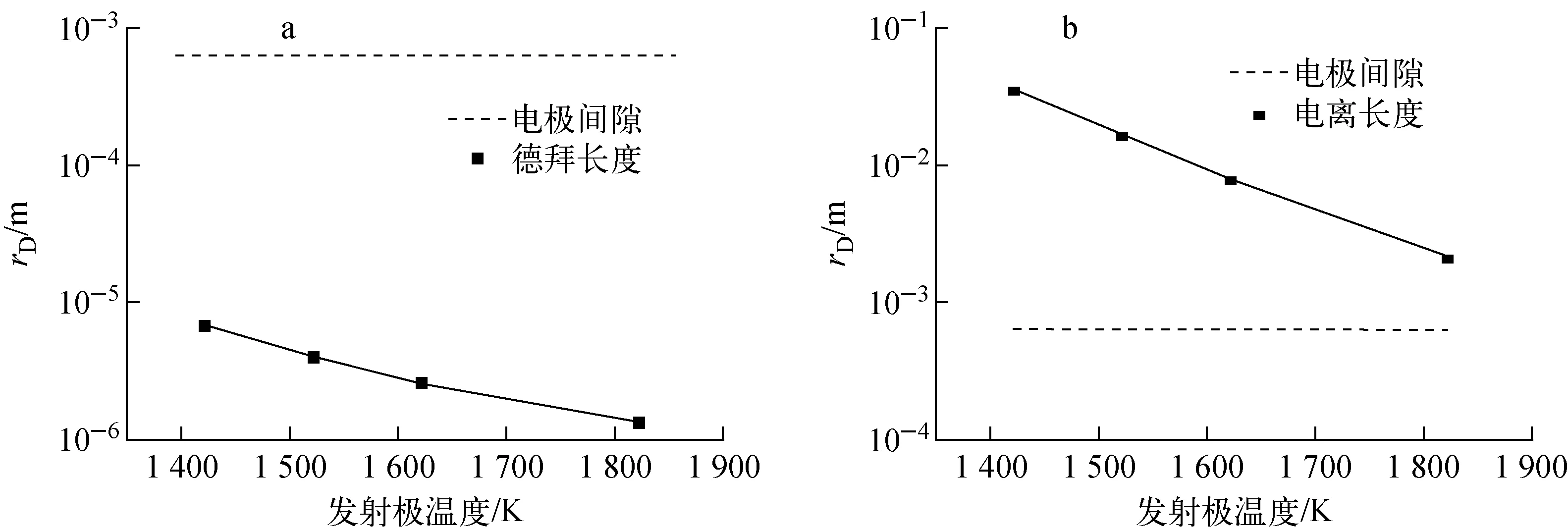
图4 不同发射极温度的等离子体德拜长度和电离长度Fig.4 Debye length and ionization length of plasma for different emitter temperatures
3.3 扩散工况区域的伏安特性
为研究电流的饱和特性,本文采用逐渐增加电流密度计算相应输出电压的方法进行伏安特性的计算,得到图5所示的伏安特性曲线(仅展示扩散工况的部分),并给出本文不同TE的计算结果与文献给出的TE=1 422 K时的实验数据的对比。结果表明,计算值与实验值符合较好,当发射极温度增至TE=1 622 K时仍呈明显的饱和电流。而当发射极温度增大到一定程度后(TE=1 822 K),输出电流呈连续上升趋势,不再呈现饱和电流的台阶。
3.4 根据电子势能分布分析电流饱和特性
由于不产生体电离,总电流中的绝大部分来自于电子电流的贡献。因此,对电子的发射与输运起决定性作用的是电子势能分布,故从电子势能分布的角度对扩散工况电流的饱和特性进行分析,其中发射极表面作为电子势能的零点。为便于叙述,从不同的发射极温度对结果分别进行讨论,其对应着不同的β(表1)。

图5 本文计算的伏安特性曲线与文献值的对比Fig.5 Comparison of U-I characteristic between this paper and lecture result
当TE=1 422 K时(β=0.001 1),电子势能分布如图6a所示,其中输出电流密度jtot=80 A/m2时的分布涵盖了电子从发射极费米面热发射输运到接收极费米面的全过程,而其他的输出电流密度为避免混淆,则略去接收极表面到接收极费米面的功函数下降段。整体而言,在准中性等离子体区,电子势能的变化较平缓,而在电极鞘层的则产生较大跃变(跃变发生的尺度仅为德拜长度的量级,为便于展示,图片对跃变的尺度进行放大)。其中,在发射极鞘层产生向上的跃变,这正是β<1的表现,且不同输出电流密度时跃变的绝对值接近VTE,这表明发射极鞘层偏离热平衡态不远;在接收极一侧,随着电流密度的增大,电子势能的跃变方式从向上跃变逐渐过渡到向下跃变,阻碍电子接收的势垒消失了。因此,输出电流增大趋于饱和的过程中,发射极鞘层电子势能的势垒决定了电子的发射最大量,即输出电流的饱和值。
当TE=1 522、1 622 K时的电子势能分布如图6b、c所示,其情况与TE=1 422 K类似。随着发射极温度升高至1 822 K(β=8.642 4)(图6d),此时β>1,离子发射过剩,发射极鞘层产生向下的跃变,对电子的发射起促进作用;在接收极一侧,与低温发射极时类似,随着电流密度的增大,电子势能的跃变方式也从向上跃变逐渐过渡到向下跃变。因此,由于发射极鞘层向下跃变的电子势能分布促进电子发射,输出电流将不断增大,不存在饱和电流,直至产生体电离而过渡到电弧工况。
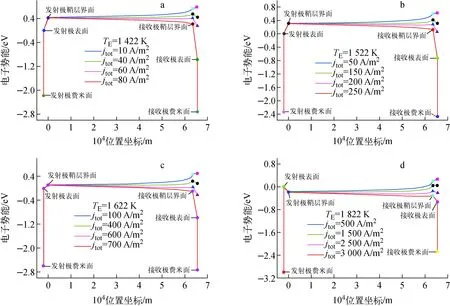
图6 TE=1 422、1 522、1 622、1 822 K时的电子势能分布Fig.6 Distribution of electron potential energy for TE=1 422, 1 522,1 622 and 1 822 K
4 结论
热离子能量转换器扩散工况饱和电流的研究对于发电诊断及电特性设计具有重要的意义。本文基于伏安特性及电极间隙电子势能分布的分析,详细讨论了饱和电流的存在性及其机理。
1) 相对于量纲简化法,通过电弧工况电离项的修正建立适用于扩散工况的输运方程,并依据发射离子裕度分析其边界条件,所得的伏安特性曲线与文献值较为吻合,说明本文的模型改进是合理的。
2) 扩散工况饱和电流的存在性由热发射的中和状态判定,其机理可通过发射极鞘层的电子势能分布来阐述。当β<1时,电子发射过剩,发射极鞘层形成电子输运的势垒,此时存在饱和电流;反之则不存在。
3) 接收极鞘层的电子势能分布随输出电流的增大发生跃变方向的改变,不影响饱和电流的存在性。
