基于MOOSE开发的中子扩散问题求解程序

牛进林，邬颖杰，郭 炯，李 富

(清华大学 核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084)

随着计算机计算能力的提升，采用全隐式耦合JFNK方法求解复杂核电厂系统已成为一个趋势。本课题组[1-4]对JFNK方法应用于高温堆耦合计算的相关关键技术进行了长期研究，取得了一系列成果，主要是基于原有程序修改其迭代方法。国外很多JFNK的研究与应用走基于平台开发的路线，以MOOSE(Multiphysics Object Oriented Simulation Environment)[5-6]平台为代表。MOOSE是由美国爱达荷国家实验室针对大规模耦合计算问题开发的开源通用平台，目前国外基于MOOSE平台开发了Pronghorn、RattleSnake、Bison、Relap7[7-12]等中子物理、燃料性能分析和系统分析程序，但这些能用于反应堆的程序对中国是出口管制的，国内目前无法获得这些程序，这使得国内基于MOOSE平台开发反应堆多物理耦合程序必须从头做起。本文基于MOOSE平台开发可用于计算中子本征值和动力学的多群扩散程序，并通过基准题进行验证。

1 MOOSE对本征值和瞬态问题的实现

1.1 MOOSE程序开发框架

MOOSE[5-6]是一面向对象的多物理耦合程序开发平台，采用鲁棒性的求解方法，具备以下能力：1) 与维度无关的用户代码，1套代码对一、二、三维问题都适用；2) 基于连续或非连续Galerkin有限元的网格离散；3) 全隐式耦合；4) 允许采用非结构化网格，包含多种形状函数；5) 很强的网格自适应性；6) 内置并行功能，用户不用开发额外的并行代码；7) 内置的后处理等。

MOOSE简化了开发多物理程序的步骤，提供了一个面向对象，包含构成模拟程序各方面的插入式系统。MOOSE程序开发包含3个层级，如图1所示，开发者只需将精力集中于中间层和顶层的开发，省去了大量重复性的底层工作，这种模块化的编程方式能大幅加快开发程序的速度，并有利于程序扩展和维护[5-6]。

图1 MOOSE层级Fig.1 MOOSE hierarchy

1.2 本征值

多群扩散本征值问题控制方程如下：

(1)

式中：D为扩散系数，cm；g为当前能群编号；g′为散射能群编号；G为最大能群数；φ为中子通量，cm-2·s-1；χ为裂变份额；Σr为移出截面，cm-1；Σs为散射截面，cm-1；Σf为裂变截面，cm-1；ν为平均有效裂变中子数；keff为有效增殖因数。

在MOOSE中，控制方程经过Galerkin有限元离散，处理成弱解形式的残差方程。为达到此目的，控制方程需要与由1组试函数构成的矩阵在求解域内进行内积。矩阵形式如下：

(2)

式中：B为基函数组；B为展开基函数；L为节点数目。将式(2)中的矩阵与式(1)进行内积得到弱解形式的残差方程(式(3))，方程的解由展开系数和基函数的积组合而成，如式(4)所示。

(3)

(4)

式中：F为非线性方程组残差；U为解向量[φg]；U为有限元展开系数；(·)表示体积分；〈·〉表示面积分。式(3)可进一步改写成式(5)形式，其中中子不考虑向上散射。

Fφ(U)=Aφ-Mφ/keff

(5)

(6)

(7)

(8)

对于本征值问题，传统是采取幂迭代法进行求解，Knoll等[13]于2009年实现了用JFNK求解本征值问题。其基本思路是在式(5)的基础上补充一个关于有效增殖因数的残差方程，如式(9)所示。

(9)

式中，Ω为整个求解域。

联立式(5)、(9)，并采用JFNK方法[14]对残差方程进行求解，从而得到本征值方程的解{φg，keff}。

在MOOSE中，物理场都是以kernel，即算子(以下统称为算子)的形式存在的。每个残差方程包含多个算子，每个算子皆对应1个C++类，只有把残差方程的所有算子都开发出来，控制方程才是完备的。式(3)包括5个算子类型，每个圆括号代表1个全求解域的算子，主要包括扩散项、碰撞移出项、群间散射源项、裂变源项；尖括号代表边界条件算子。虽然每个能群残差方程的算子类型会有重复，但由于群截面和物性的不同，都需重新定义本能群的算子。而相关的物性需在额外的物性模块定义，需有相关的C++类相匹配。目前已实现了多群扩散方程各算子的开发，完成了常物性开发，也实现了与变量耦合的变物性。式(9)的残差方程是MOOSE提供的，不需要额外开发。

陈大勇睁圆了双眼，双手握紧鬼子的枪刺，一声虎啸，刺刀被他带着喷血拔了出来，小鬼子惊呆了，手一撒，就那么两秒的时间，陈大勇反手把刺刀扎进了鬼子的胸膛。

1.3 瞬态计算

考虑多组缓发中子的多群扩散瞬态方程如下：

g=1,2，…，G

(10)

k=1,2，…，K

(11)

式中：C为缓发中子先驱核浓度，cm-3；keff,0为系统初始时刻的有效增殖因数；v为当前群中子平均速度，cm/s；k为缓发中子先驱核组标；K为缓发中子先驱核组数；λ为缓发中子先驱核衰变常量，s-1；β为缓发中子总份额；βk为第k组缓发中子先驱核份额。

将式(10)、(11)在求解域分别与式(2)进行内积，得到弱解形式的残差方程：

(12)

(13)

联立式(12)、(13)，采用JFNK方法对残差方程进行求解，得到瞬态方程的解{φ，C}。

在本征值程序的基础上，残差方程(12)主要是增加了瞬态项和缓发中子源项，裂变源项因缓发中子的缘故需重新调整；开发了缓发中子残差方程(13)的相关算子和物性。

1.4 预处理矩阵

(14)

式中：J为雅可比矩阵；N为预处理阵；v为子空间基向量；ε为差分步长。

目前程序中预处理阵采用块对角矩阵形式，不考虑不同变量间的耦合关系。本征值问题采用的预处理阵为式(15)，瞬态问题采用的预处理阵为式(16)。

(15)

(16)

(17)

Nkeff,keff=1

(18)

NCk,i,Ck,j=(Bi,λkBj)

(19)

式中，i、j分别为试函数和展开基函数的组标。

1.5 边界条件

MOOSE提供了第1类和第2类边界条件的接口，但缺乏真空边界条件和反照率边界条件。因此开发这两个边界条件的接口对中子计算是很有必要的，现已在程序中完成了真空边界条件和反照率边界条件的接口开发。对于反照率边界条件，在边界处满足式(20)。

(20)

式中，α为反照率。当反照率取0时，得到真空边界条件，如式(21)所示。

(21)

1.6 MOOSE实现

基于MOOSE开发的中子程序基本框架如图2所示，中间淡蓝色框图是MOOSE的基本框架，外围灰色部分是1.2～1.5节的内容在MOOSE基本框架下的实现，也是程序开发的核心，其中中子扩散方程、缓发中子方程、边界条件、物性参数、预处理器是构成中子程序开发的关键技术难点。目前尚无专门的截面库与本程序对接，现阶段是根据特定问题的截面信息定制一套物性参数。MOOSE提供了多种预处理的接口，除块对角预处理外还有有限差分预处理、基于物理的预处理等，目前在本程序中主要是实现块对角的预处理方式。式(3)、(12)、(13)的各物理场算子构成了程序的基本模块，将各基本模块按照问题需求在输入卡中像搭积木一样“拼接”起来便构成了基本程序，如图3所示，本征值问题和瞬态问题所需的基本模块是不完全一致的。中子程序流程图如图4所示。

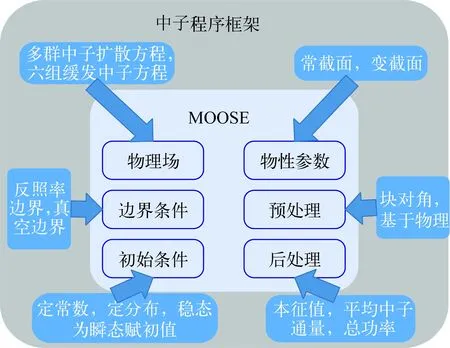
图2 中子程序框架Fig.2 Neutron program diagram

2 数值验证

通过2D-TWIGL基准题[15]对程序进行验证。本基准题包括1个稳态算例和2个瞬态算例。

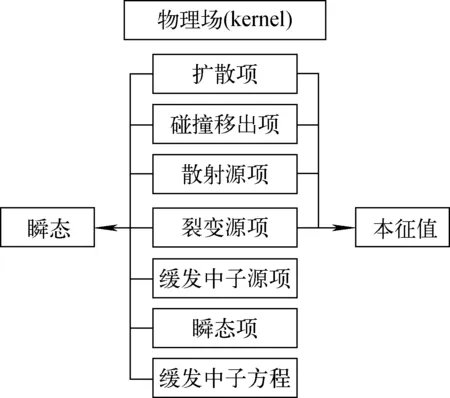
图3 模块化程序架构Fig.3 Modularized program architecture diagram

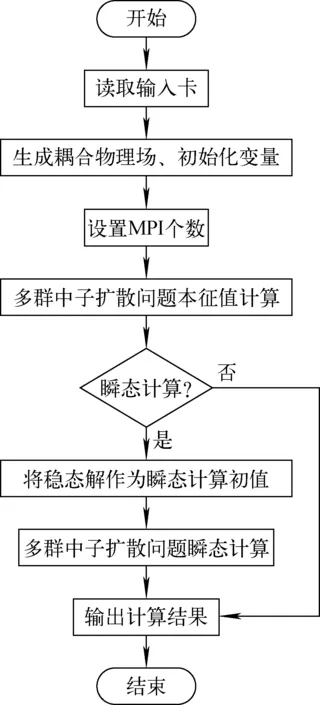
图4 中子程序流程图 Fig.4 Neutron program flow diagram

2.1 基准题描述

TWIGL基准题是一简化的二维双群扩散加1组缓发中子的动力学问题。反应堆是正方形的，边长160 cm，包含3个物质区域，其1/4堆芯几何模型和边界条件如图5所示。其截面参数列于表1。缓发中子先驱核的份额为0.007 5，衰变常量为0.08 s-1。

图5 TWIGL基准题几何模型Fig.5 TWIGL benchmark geometry

2.2 本征值计算

采用结构化网格，共6 561个网格点，6 400个有限元，如图6所示。本征值计算结果为：数值解0.913 20，参考解0.913 21[15]，两者间相对误差为0.001%。可见计算结果与参考解符合得很好，精度很高。快群和热群中子通量分布如图7所示。MOOSE提供幂迭代(PI)求解本征值和用切比雪夫加速的接口，1次幂迭代也可看作1次非线性迭代。JFNK求解本征值和经过契比雪夫加速的幂迭代进行对比，求解的本征值是相同的，计算性能结果对比列于表2，残差收敛结果对比示于图8，发现在同样的收敛精度下，JFNK能大幅减少非线性迭代的步数，从而大幅减少计算时间，计算效率提高接近1个数量级。另外可看出，即使经过契比雪夫加速，幂迭代的残差在非线性步也不是单调下降的，在小范围会有波动上升。

表1 TWIGL截面参数Table 1 TWIGL cross section parameter

2.3 瞬态计算

采用一阶向后欧拉差分处理时间项，以稳态为初始时刻。考虑两个瞬态工况：1) 物质区1的热群吸收截面在0时刻突然减少0.003 5 cm-1，而后物性保持不变，模拟0.5 s(工况1)；2) 物质区1的热群吸收截面从0时刻开始，在0.2 s时间内线性减少0.003 5 cm-1，而后物性保持不变，模拟0.5 s(工况2)。两个工况的时间步长均分别选取0.01、0.05、0.1 s，参考解[15]时间步长为0.001 s，模拟结果与参考解的对比示于图9。可看出，无论是急速瞬变还是缓慢瞬变，程序的跟踪能力都很好，数值结果和模拟结果相一致；时间步长取0.01 s和0.05 s时，结果的精度也是有保障的；时间步长取0.1 s(参考解时间步长的100倍)时，结果会出现一些偏差，这是由于时间步长如果取得过大，时间离散带来的误差就会变大，因此需要综合考虑时间离散带来的误差和计算效率来选取时间步长。

图6 TWIGL基准题网格Fig.6 TWIGL benchmark mesh

图7 快群和热群中子通量分布Fig.7 Fast neutron and thermal neutron flux distribution

表2 JFNK和幂迭代计算性能对比Table 2 Performance comparison of JFNK and PI

3 结论

本文基于MOOSE平台开发了可用于中子扩散的求解器，采用JFNK方法计算本征值问题和瞬态问题，开发了反照率边界条件和真空边界条件接口。通过基准题TWIGL验证，发现对于本征值问题，JFNK方法精度高、收敛快，与传统的采用切比雪夫加速的幂迭代方法相比，能大幅减少非线性步的数量，极大提高计算效率。对于瞬态问题，瞬变的跟踪能力强，在较大的时间步长下，也能保证一定的精度。

图8 残差收敛性对比Fig.8 Residual convergence comparison

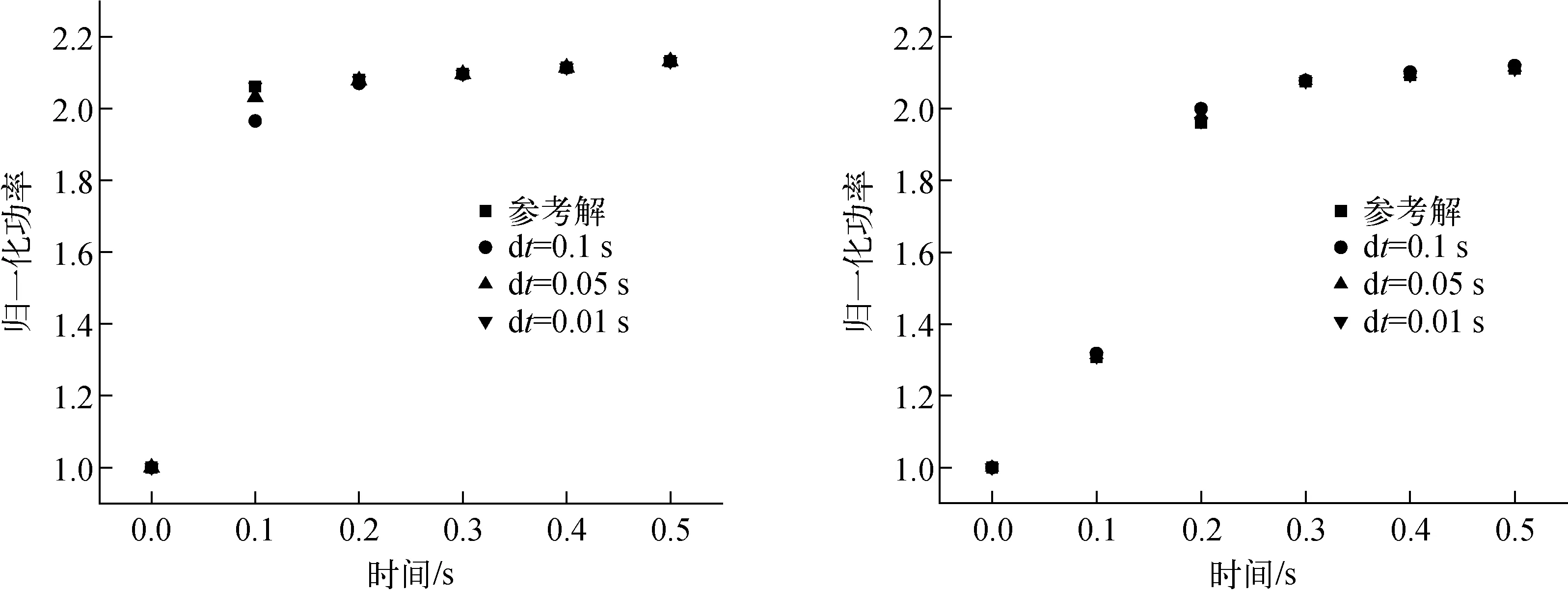
图9 两个工况的结果对比 Fig.9 Result comparison of two operation conditions

本程序具有基于MOOSE平台开发程序的优势，1套代码能解决多维问题，对规则几何或不规则几何都有强大的模拟能力，能很方便地进行并行计算等。之后还可对程序进行进一步的优化，如选取不同的预处理矩阵、采用高阶有限元、高阶时间步长、并行计算等，从而不断提高求解精度和计算效率。在未来的研究中，中子程序可与热工计算在同一框架下进行全隐式耦合，为实现反应堆的多物理耦合计算提供支持。但现阶段还没有可与中子程序对接的核数据库接口，限制了程序的模拟能力，这也是需要重点解决的问题。