数控加工中心主轴热误差预测模型建模的研究*

王 谦 周圣强

（宿州职业技术学院 安徽宿州 234101）

热误差补偿的前提是能够对某一温度场的机床热误差进行准确地预测，然后根据预测值进行热误差补偿，这就要求所建立的热误差模型要具有较高的准确性。热误差建模是建立起运动轴热误差与各个热敏感点温度值之间的关系所依托的数学模型的过程，因此建模所依托的数学理论在热误差建模和补偿中至关重要。热误差建模依托的数学理论常用的有多元线性回归理论、滞后变量理论、神经网络理论、支持向量机理论等。支持向量机理论是近期发展起来的一种数学分析方法，常用于对小样本数据的分类和回归，支持向量回归算法能够通过对小样本数据的学习建立决策函数，从而实现对未知数据的预测。文章在已做研究工作（以BV850数控加工中心为例，为其组建了温度和热误差集成检测系统，并通过一定的方法筛选出两个热敏感点S1和S6）的基础上，对热误差建模现有理论进行了大量的阅读和研究，分析和阐述了运用多元线性回归理论、分布滞后理论和最小二乘支持向量回归机理论对加工中心主轴热误差建立预测数学模型的方法。

1 多元线性回归理论建模

多元线性回归是在进行热误差建模时经常被国内外学者使用的一种统计学中的传统方法。它是在掌握大量观察数据的基础上，用统计方法寻求多输入和单输出之间的函数关系，该方法以假设因变量和自变量成线性关系为应用基础，假定线性回归成立于因变量和自变量之间，建立回归函数表达式。

以多个热敏感点的测量温度值为自变量，以加工中心主轴热误差为因变量建立模型，便可建立主轴热误差的多元线性回归函数模型。假设加工中心筛选出了k个热敏感点，有n个测量值，其通用表达式为：

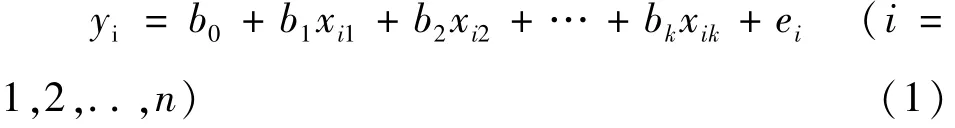
式中，yi为热误差测量值，xi1，xi2，…，xik为热温度敏感点温度测量值，b0，b1，…，bk为回归系数，ei是与实际观察值yi存在的偏差，也称为残差。

多元线性回归模型中的回归系数可利用最小二乘法［1］求得，最小二乘法是拟合其系数的一种常用方法，参数b0，b1，b2，…，bk的最小二乘估计为：

式（2）中

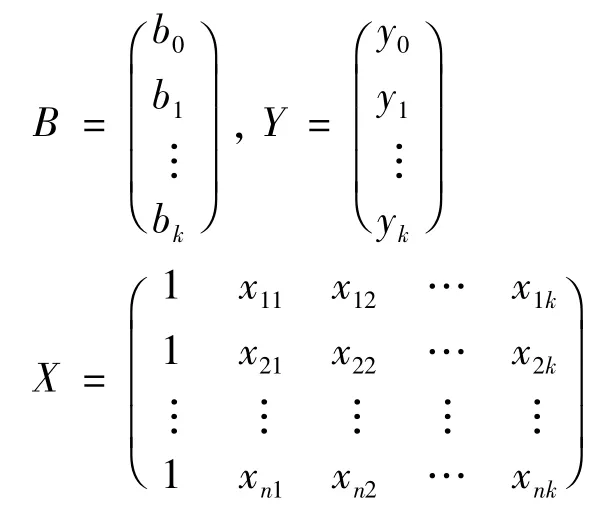
通常情况下，在多元线性回归模型建立后要进行拟合精度评估，通过残差平方和计算出模型标准差，可用来评定全部观测值与回归估计值的偏离程度，其计算公式为：

多元线性回归模型的精准度在很大程度上会受到温度测量数据的影响，因此，该模型在实验和建模中对传感器的质量提出了较高的要求。另外，该模型的精准度还会受到多重共线性问题的影响，使用这项技术要面对的一个难点就是如何合理选择建模用温度变量。

将上述建模理论应用于加工中心主轴热误差建模，以主轴热误差为因变量，以热敏感点S1和S6的温度值为自变量建立多元线性函数，就是建立加工中心主轴热误差的多元线性回归模型，其表达式为：

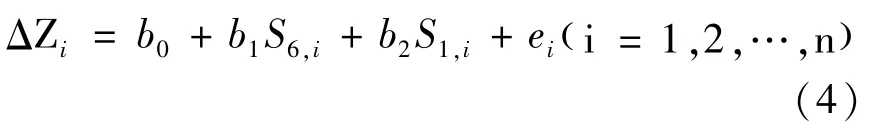
式（4）中，ΔZi—数控加工中心主轴轴向热误差第i次预测值，b0—常数项系数，通过分析计算实验数据，使用最小二乘法求解式（4）中的b0，b1，b2，可求出最终表达式。

2 分布滞后理论建模

若在函数表达式中因变量不仅会受到若干解释变量当前值的影响，还会受到解释变量若干滞后值的影响，则这种关系的数学模型可以用分布滞后模型来描述。分布滞后模型是在多元线性回归模型的基础上发展而来的，在多元回归模型的基础上分布滞后模型的建模自变量新纳入了解释变量的滞后项。由于在数控机床热误差检测实验中，温度值的采集在温度传感器上通常表现出一定的滞后反应，考虑到在热传导过程中机床主轴温度存在的这种时滞性，在机床热误差建模中采用分布滞后模型，将有助于提高数控机床热误差建模的精度。

分布滞后模型的通用表达式为：

式（5）中，Yt—因变量α0—常数，n—最大滞后期u—外生变量个数，由于在实验中有较多的数据测量值，可采用简单的权宜估计法实现滞后阶数n的确定。取，n＝1，2，…，i，对不同条件下的i采用最小二乘法来进行拟合，当有一个滞后变量的系数改变符号，或滞后变量的回归系数开始变得统计不显著时，最终的滞后阶数就是i-1。

式（5）中，由于xt与xt-1，xt-2，…，xt-n相关性很强，多重共线性问题有可能会出现［2］，从而导致对该模型回归系数βi的估计不够准确。虽然对单个βi的估计存在一定偏差，但是对因变量yt构成长期影响的是分布滞后模型βi的和以及xt的变化，因此在整体上并不影响分布滞后模型yt的估计精度：

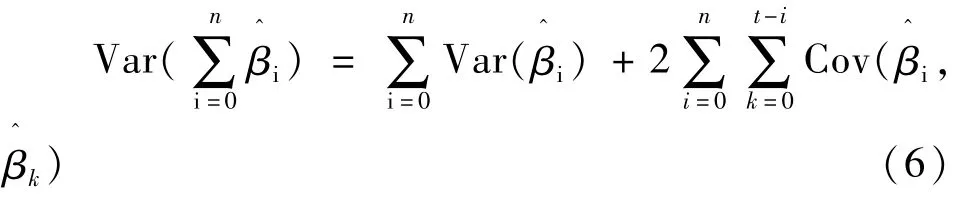
实际应用中协方差项通常为负数，在这些项同时为负值且绝对值很大时，Var）一般小于，因此βi的和有着较高的估计精度。式（6）中自变量和自变量的滞后项一般成正相关。

自变量和自变量的滞后项通常成正相关，将上式及上述建模理论应用于数控加工中心主轴热误差建模，设定滞后期为2阶，可得数控加工中心主轴热误差分布滞后回归模型的表达式为：

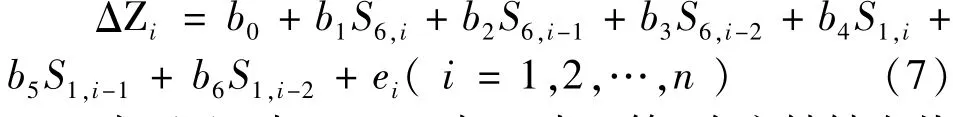
式（7）中，ΔZi—加工中心第i次主轴轴向热误差的预测值，b0—常数项系数，通过分析计算实验数据，使用最小二乘法求解式（7）中的b0，b1，…b6，可求出最终表达式。

3 最小二乘支持向量机回归理论建模

传统的统计理论是已知样本的分布形式，通过对大量数据的运算分析，确定相应参数，以实现统计建模。支持向量回归机是一种新兴的基于数据的机器学习方法，能够在数据分布未知的情况下通过对少量样本的分析学习实现对未知数据的预测。

3.1 支持向量机理论

统计学家Vapnik建立了一种专门分析机器学习在小样本情况下的规律的理论，即统计学习理论，支持向量机就是在此理论基础上发展形成的一种新的机器学习算法。支持向量机能够根据有限的样本信息通过最小化结构风险原理来进行机器学习，提高泛化能力，在解决小样本、高维数、非线性等复杂问题上有特有的优势，在解决模式识别、函数拟合等机器学习问题上表现出了优秀的性能［3］。将支持向量回归机模型用于数控机床的热误差建模，不光能提高模型的精度和泛化能力，还能减小模型对数据量的需求，节约实验成本。

最小二乘支持向量机是支持向量机的一种扩展，该方法将损失函数替换为最小二乘线性系统，用等式约束替换不等式约束，从而可以用线性运算的方法进行运算，经由这个适当的处理，该模型的计算复杂度得到大大降低，求解速度得到显著加快。

3.2 热误差的回归问题

回归分析就是对测量数据进行函数估计，它的最终目的是通过对已知数据的计算分析寻求能够反映输入输出关系的函数关系

3.3 最小二乘支持向量机回归算法

设训练样本集D=k＝1，2，…，}N，xk∈Rn，yk∈R，yk为输出数据，xk为输入数据。原始空间（权ω空间）里的函数估计问题能够转化为求解下式：

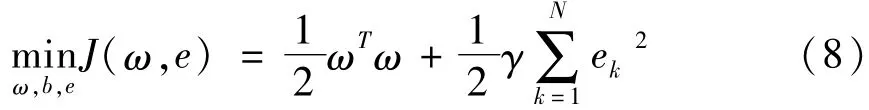
约束条件为：yk＝ωTφ（xk）+b+ek，k＝1，2，…，N。

式中，φ（xk）：Rn→Rnh为核空间映射函数，ω∈Rnk为权矢量，ek∈R为误差变量，γ为可调函数，b为偏差量，SSE误差和规则化量之和为损失函数J。

为解决原始空间中线性不可分的问题，可以引入核空间映射函数，核空间映射函数可以通过在原始空间里抽取特征，完成从原始空间里的样本到高维特征空间里的向量的映射。根据式（8），拉格朗日函数可定义为：

L（ω，b，e；a）＝

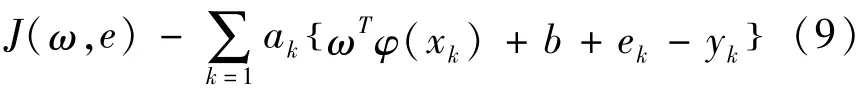
式（9）中，ak∈R为拉格朗日乘子。

优化上式，让L对ω，b，ek，ak求偏导数并令其为0，消去变量ω，e，可得矩阵方程：

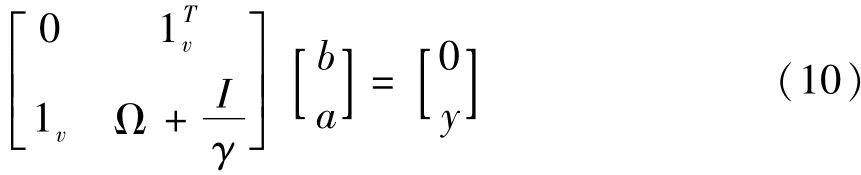
根据Mercer条件，存在核函数Ψ（xk，xl）和映射函数φ，使得：

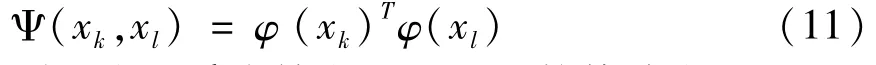
则最小二乘支持向量机的函数估计为：

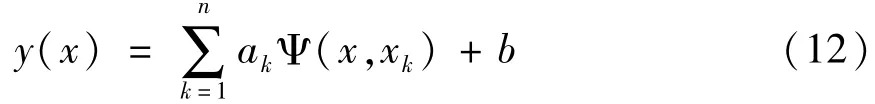
通过式（12）可求解出a，b，满足Mercer条件的任意对称函数均可选作核函数Ψ（xk，xl），可采用线性核、多项式核、RBF核等。

3.4 核函数

对于非线性映射的特征空间，其内积计算量是惊人的，而通过核函数的转换能巧妙地解决这个问题，只要找到满足条件的核函数，就能把输入空间中线性不可分问题映射到一个特征空间而成为线性可分的问题，从而使非线性问题得到简化［4，5］。要进行加工中心主轴热误差非线性支持向量回归机的建模，必须选择最佳核函数将加工中心温度测量值序列映射到高维特征空间，然后对决策函数进行求解。常用的核函数有线性核函数、多项式核函数和高斯径向基（RBF）核函数等，其表达式如下所示：

（1）线性核函数：

（2）多项式核函数：

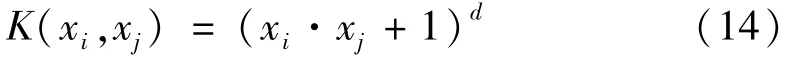
表示一个d阶多项式核

（3）RBF核函数：

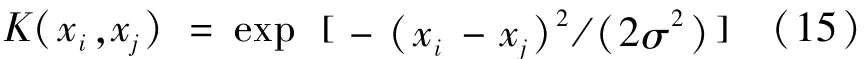
式（15）中，σ为核函数的宽度，将1／σ2记为参数敏感系数g。在核函数中，一般选择RBF核，RBF核用于建模具有训练速度快、精度高等优点。文章也优先选择RBF核用于热误差建模，训练结果的预测精度和稳健性取决于参数敏感系数g和惩罚系数的取值。

4 结语

（1）多元线性回归模型具有建模快捷、计算方便、结构简单等特点，基本上能够满足普通数控机床热误差补偿精度的要求。但是采用多元线性回归模型进行建模，在建模样本不是很充分的情况下，多重共线性的问题有可能会出现，导致计算结果不稳定，得到的结果跟理想值相差较大。

（2）由于加工中心结构的影响，温度传感器对温度的测量具有滞后的效应。分布滞后模型将自变量、自变量的滞后项均纳入建模，体现了温度传感器对温度采集的滞后现象，使拟合精度得到了一点提升，但分布滞后模型没有将因变量的滞后项也纳入建模，而因变量的滞后项才能对未来数据进行预测，所以分布滞后模型的精度不高。

（3）支持向量机可以通过对小样本数据的学习达到预测未来数据的目的，它具有非线性映射理论基础，利用核函数代替高维非线性映射，在解决非线性问题上表现优秀。在支持向量机的基础上进行扩展形成最小二乘支持向量机，它通过适当的变换大大简化了支持向量机的计算复杂度，降低了计算成本。在数控机床的热误差建模中采用最小二乘支持向量回归机，不光能保证良好的建模精度和泛化能力，还能减小模型对数据量的需求，节约实验成本。