基于Android系统的电子分度表软件设计

郭向霞 周伟建 俞利明 陈青峰

(浙江中控自动化仪表有限公司)

在工业控制领域中，温度是测量频率较高的物理参数，而常用的温度测量传感器主要有热电偶和热电阻。以热电偶为例，在使用热电偶测量温度时，测得电动势后，需要将电动势的值转换成温度，而目前的主要方式是查询由热电偶的电动势和温度列成的表格，即热电偶分度表。热电偶根据所使用材料的不同分为多种型号，每种型号有各自的分度表，查询时很容易出错。另外由于热电偶分度表是在参考端温度为0℃时制定的，而在实际使用环境中，参考端温度通常不为0℃，这就需要工作人员再次进行手动换算。同时由于分度表中是以1℃为分割的，如果需要查询非整数的温度值，仍需要根据前后两个值进行换算。综上所述，查询分度表的表格非常不方便，迫切需要开发一个分度表查询软件来解决用户的不便。目前也有一些PC版本的查询分度表软件，但是操作人员在现场作业时仍需要携带电脑。考虑到目前Android智能手机的普及性，笔者设计开发了一款基于Android系统的分度表双向查询软件，可以满足操作人员随时随地查询分度表的需求。

1 软件特点

本软件基于Android系统开发，对使用环境没有限制，任何Android系统的手机、平板电脑都可以安装使用。本软件有以下特点：

a.支持10种标准型号热电偶分度表查询，分别是 R 型、S型、B 型、J型、T型、E 型、K 型、N型、C型、A型；

b.支持6种标准型号热电阻分度表查询，分别是 Pt100、Pt200、Pt500、Pt1000、Cu50、Cu100；

c.可以查看每种测温元件的有效测温范围，帮助工作人员选型；

d.对于热电偶，支持输入冷端补偿的温度值，解决现有分度表只能查询冷端温度为0℃的问题；

e.支持输入非整数的温度值，解决现有分度表只支持查询1℃分割的问题；

f.支持温度或者电动势、电阻超限时的提示；

g.支持双向转换，对于热电偶可以根据设置的冷端值，由温度换算成电动势或者由电动势换算成温度，对于热电阻可以由电阻值转换成温度值，或由温度值转换成电阻值。

2 软件实现

本软件的开发语言是JAVA，设计采用MVC模式，实现界面、逻辑、数据的解耦。因此软件开发分为3个部分：界面（UI）、控制和转换算法。

UI设计时除了满足功能特点外，还需要考虑到工业现场操作的友好性，为此自定义了下拉控件，实现分度号类型的选择。

控制层考虑到其可扩展性，使用面向对象的多态性原理，设计一个抽象基类定义各子类需要实现的抽象方法，有正向和逆向转换方法，有1个热电偶基类、1个铜热电阻基类和1个铂热电阻基类，热电偶各子型号继承热电偶基类，铜热电阻各子型号继承铜热电阻基类，铂热电阻各子型号继承铂热电阻基类。基类实现抽象基类需要实现的公共转换方法，各子类实现各自个性数据的存储和转换算法，这样后期如需要增加铂热电阻的子型号，只需要新增一个子类，继承铂热电阻基类，在子类里定义其特有的参数和方法,然后把类型和其转换控制类绑定即可实现相应类型的分度表转换。

算法部分主要实现热电偶和热电阻不同型号的分度表双向转换。GB/T 16839.1—2018给出了热电偶各型号的转换公式，算法只需要用代码实现即可。JB/T 8623—2015和 GB/T 30121—2013只给出了热电阻温度转电阻的转换公式，而由电阻转温度的转换公式，笔者研究了多项式拟合和牛顿迭代法两种实现方式。以下部分给出各算法的公式和关键程序段。

2.1 热电偶

根据GB/T 16839.1—2018，不同型号的热电偶电动势转温度公式是［1］：

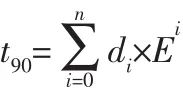
式中di——多项式第i项的系数；

E——电动势，μV；n——多项式阶数；

t90——ITS—1990温度，℃。K型热电偶0～1 300℃温度范围内,温度转电动势公式是［1］：

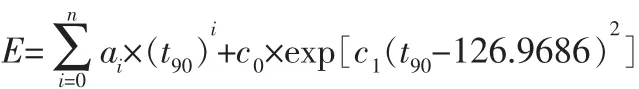
式中ai——多项式第i项的系数；

c0、c1——常数项，参考GB/T 16839.1—2018表8。

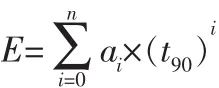
其他型号和K型热电偶-270～0℃温度范围内,温度转电动势的公式是［1］：根据分层设计原则，热电偶基类里实现公共的转换公式而不同型号的热电偶参见GB/T 16839.1—2018表2～11设置各自的参数n和a0～an的值，然后调用公用的方法计算。

计算温度和电动势的关键算法如下，其中需要调用数学函数Math.pow(x,y)来计算(t90)i或者Ei：public double calculate(double param,int count){

double d=0.0d;

for(int i=0;i＜=count;i++){

d+=this.a［i］ *Math.pow(param,i);

}

return d;

}

2.2 热电阻

根据JB/T 8623—2015，工业铜热电阻温度转电阻换算公式是［2］：

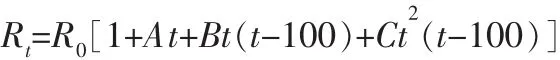
根据GB/T 30121—2013，工业铂热电阻温度转电阻换算公式是［3］：式中A、B、C——常数；

R0——温度为0℃时的电阻，Ω；

Rt——温度为t时的电阻，Ω；

t——温度，℃。

由于铜热电阻和铂热电阻各分度号只有0℃时的电阻值不同，转换公式是相同的。因此只需要在各自基类里实现公式，各子类传入R0值即可。以铂热电阻为例，其温度转电阻的算法如下：

//铂热电阻温度转电阻的算法

double fromTempSub（double param） {

if （（param >= -200.0） && （param ＜=0.0d）） {

return this.R0 * （1.0d + this.A *param+this.B*param*param+（this.C

* （param-100）

*param

*param

*param））；

}

if （（param>0.0d） && （param ＜=850.0d）） {

return this.R0*（1.0d+this.A*param+this.B

*param*param）；

}

return overError（）;

}

由于热电阻温度转电阻的公式是高阶多项式，直接求解比较困难，因此笔者提出两种解决方案，一种是把温度和电阻对应的样本数据通过曲线拟合，生成电阻和温度对应的多项式，另一种是通过牛顿迭代法来求解复杂方程的根。

2.2.1 曲线拟合方法

曲线拟合是要求拟合的曲线能大致模拟数据的基本趋势，其准确性判别准则也有很多，如偏差的绝对值之和最小、偏差的最大绝对值最小或偏差的平方和最小，偏差的平方和最小也叫最小二乘法，经常采用最小二乘法来确定多项式的系数，拟合工具可以选择Matlab、Excel等，拟合过程不再细述，以下为Pt100拟合的多项式算法：

//Pt100电阻值转温度算法

public double toTempSub（double param） {

if （（param >=18.52） && （param ＜ 100）） {

return 1.7237E-08*param*param*param*param-9.9584E-06*param*param*param+2.8581E-03*param*param+2.2161*param-241.96;

}else if （（param >= 100） && （param ＜=390.49）） {

return （1.7571E-09） *param*param*param

*param-3.0900E-07*param*param*

param+9.9568E-04*param*param

+2.3592*param-245.8;

}

return overError（）;

}

2.2.2 牛顿迭代法

牛顿迭代法是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,是把非线性方程f（x）=0线性化的一种近似方法。迭代关，其 中f（x）是 正 向 方 程 ，nf′（xn）是f（xn）的一阶导函数。 以Pt100（-200～0℃）温度转电阻的公式为例：

牛顿迭代法计算步骤为：

a.选初始近似值x0，计算f0=f（x0）,f′0=f′（x0）；

c.如果abs（xi-xi-1）满足设定的误差值，则终止迭代，否则转到步骤d；

d.如果迭代次数达到预先指定的次数N,或者 f′i=0，则方法失败，否则以（xi+1，fi+1，f′i+1）替代（xi， fi,f′i）并转到步骤b继续迭代。

通过对比两种算法的精确度，软件最终使用牛顿迭代法实现电阻到温度的转化,其精度可达10-7，迭代次数为4次左右，算法效率较高。

3 结束语

笔者开发的基于Android系统的分度表软件，对于热工操作人员有极大的帮助。笔者应用的曲线拟合技术和牛顿迭代算法对其他应用领域也有很好的启发。为了提高数据计算的精确度，曲线拟合的系数需要在合理范围内做些许调整，牛顿迭代算法也需要选取合适的初值，才能满足收敛性。作为一个可以实际应用的软件，软件设计过程中也充分考虑了容错性、可扩展性和友好性。