基于围线积分引理的信号变换域分析方法*

陈绍荣，何 健，陈柏良，薛在阳

（1.陆军工程大学通信士官学校，重庆 400035；2.军委装备发展部军事代表局驻成都地区军事代表室，四川 成都 610041；3.深圳市惟新科技股份有限公司，广东 深圳 518000；4.奥特斯科技（重庆）有限公司，重庆 401133）

0 引 言

早期的《信号与系统》著作[1-2]涉及复平面上的围线积分引理，由于对围线积分引理条件的叙述不严谨，因此使用时缺乏可操作性，在查阅有关《复变函数》著作[3]及近期的《信号与系统》著作[4]的基础上，证明了围线积分引理，基于围线积分引理，研究了s域卷积运算问题，给出了利用区左极点或区右极点计算s域卷积的留数方法；依据连续时间非周期信号的ILT导出了非周期序列的IZT，基于围线积分引理，给出了利用区外极点计算有终序列的IZT及计算z域卷积的留数方法，提出了利用两个连续时间信号各自的双边LT来计算时域卷积信号及积信号相应样值序列的双边ZT的方法。

1 围线积分引理

设CR是s平面上半径为|s|=R的圆周，CABC是CR上的任意一段圆弧，如图1所示。

图1 s平面上围线积分引理示意图

若函数F(s)在圆弧CABC上连续，并且满足条件：

则有：

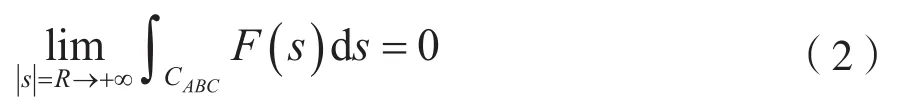
证明：

在圆弧 CABC上，令 s=Rejθ，则 ds=jRejθdθ，因为，所以对任意ε＞0，存在充分大的正数R0，当|s|=R＞R0时，则有：

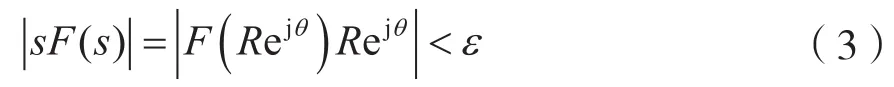
考虑到式（3），则有：

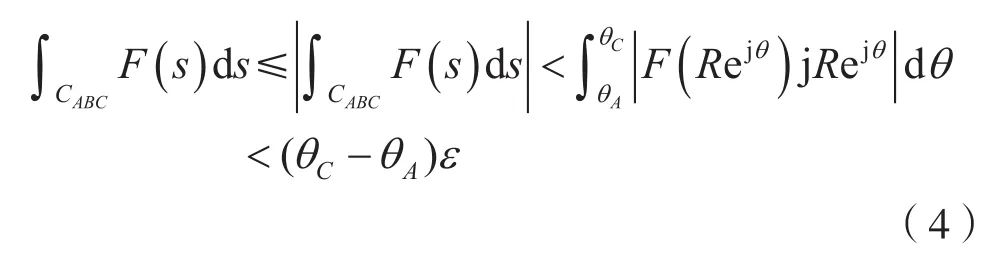
由式（4）可知，式（2）成立。

结论1：

若函数F(s)在CR上连续，并且则有：

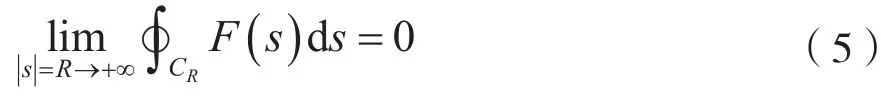
2 基于围线积分引理的信号变换域分析方法

2.1 基于围线积分引理及留数定理计算s域的卷积积分

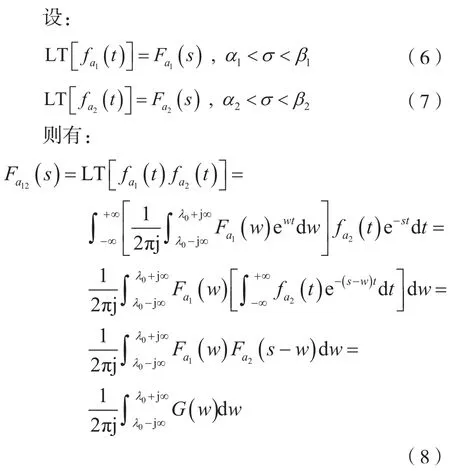
式中，G(w)=Fa1(w)Fa2(s-w)，w=λ+jΩw，s=σ+jΩ，考 虑 到 α1＜λ＜β1，α2＜σ-λ＜β2， 则 α1+α2＜σ＜β1+β2。λ0位 于 G(w)的 收 敛 域 λ1＜λ＜λ2之 内， 其 中，λ1=min(α1,σ-β2)，λ2=min(β2,σ-α2)。

设CR是w平面上半径|w|=R的圆周，CABC（CADC）是CR上的逆时针（顺时针）方向的一段弧，如图2所示。

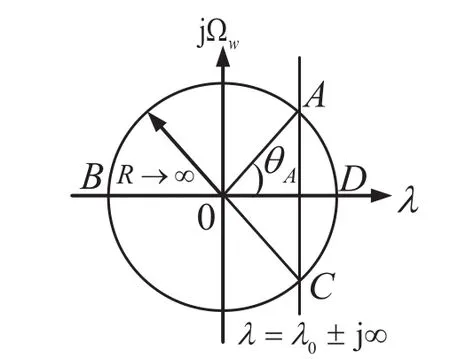
图2 w平面上围线积分引理示意图

由围线积分引理可知，若函数G(w)在CR上连续，并且满足条件：

考虑到式（10），则式（8）可对G(w)的区左极点wi(i=1,2,…,p1)（Re[wi]≤λ1的极点），利用留数定理进行计算，即：

考虑到式（11），则式（8）也可对G(w)的区右极点wj(j=1,2,…,p2)（Re[wj]≥λ2的极点），利用留数定理进行计算，即：

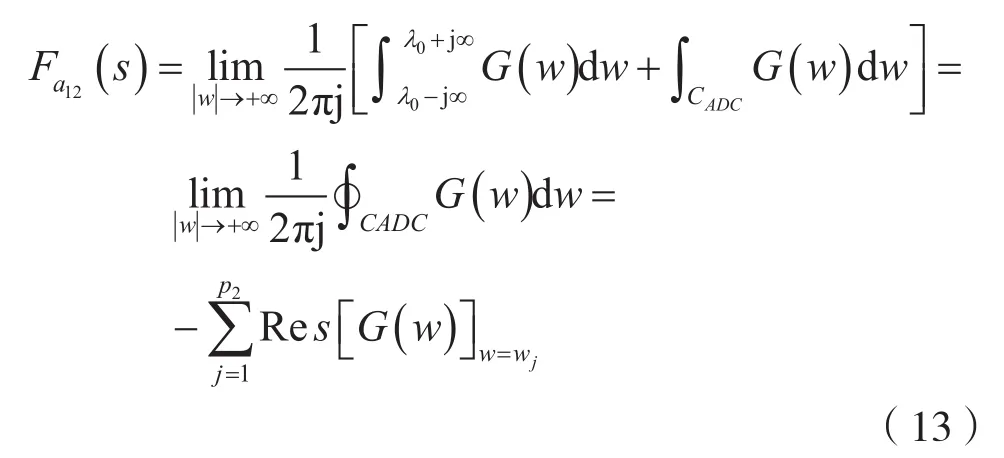
式（13）中的负号是由于围线绕行方向为负向（即顺时针方向）的缘故。

若G(w)的区右极点数目较少时，适宜用式（13）进行计算，否则，适宜用式（12）进行计算。

2.2 基于围线积分引理及留数定理计算IZT

考虑到：

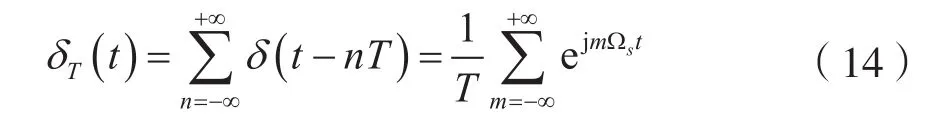
式中，Ωs=2π/T。

对连续时间信号fa(t)抽样，其样值信号f^(t)可写成：

设：

考虑到式（16），对式（15）两边取双边LT，可得：

其实，式（17）还可写成：

式中，f(n)=fa(nT)，z=esT，并且：

称F(z)为序列f(n)的z变换（ZT），也称F(z)为序列f(n)的象函数。

考虑到连续时间信号fa(t)的双边LT的象函数Fa(s)的收敛域为α＜σ＜β，因为z=esT，所以象函数F(z)的收敛域为 Ra=eαT＜|z|＜eβT=Rb。并将 F(z)的 |z|≤Ra的极点称为区内极点，将F(z)的|z|≥Rb的极点称为区外极点。

考虑到式（17），由式（18）可以得到：

考虑到式（20）及拉普拉斯逆变换（ILT）式，则有：

式（21）称为象函数F(z)的逆z变换(IZT)，其中，c1为T(z)=F(z)zn-1的收敛域内的正向闭曲线。

先在z平面上F(z)的收敛区域Ra＜|z|＜Rb内画一条正向圆周曲线c1，再引入一条半径为无穷大的圆周曲线c2，最后选取一条将T(z)=F(z)zn-1的所有区外极点zp包括在内的积分路径，如图3所示。

图3 z平面上极点的围线积分路径示意图

设

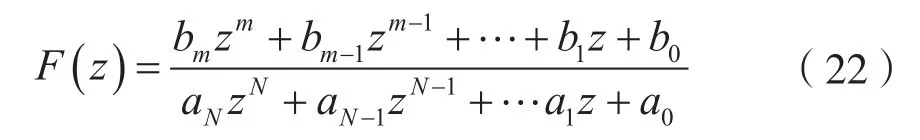
式中，ai(i=0,1,2,…,N)和bj(j=0,1,2,…,m)为常数。

令q=N-m，T(z)=F(z)zn-1，若n≤q-1，即q-n≥1时，则有：

由于式（23）满足围线积分引理的条件，因此，有：

由图3可知，对区外极点zp(p=1,2,…,n2)作逆z变换时，沿闭曲线积分的路径由4段构成，它们分别是c1、c2、d1及d2。因为d1+d2线段的积分恒等于零，由式（24）可知，沿着c2的积分也恒等于零，于是逆z变换(IZT)可用下式计算，即：

式中，ε(n)为单位阶跃序列，zp(p=1,2,…,n2)是T(z)=F(z)zn-1的区外极点（即T(z)在正向闭曲线c1外的极点），n2为区外极点数目，负号是因所有的区外极点zp始终在积分路径c1右侧的缘故；vi(i=1,2,…,n1)是T(z)=F(z)zn-1的区内极点，n1为区内极点数目。

2.3 基于围线积分引理及连续时间信号的双边LT确定相应序列的双边ZT

考虑到拉普拉斯逆变换式，则式（19）可写成：

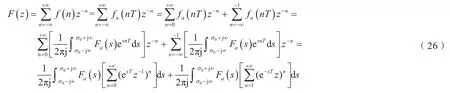
则式（26）可写成：

可见，式（28）中的第一部分仅与Fa(s)的区左极点（Re[s]≤α的极点）有关；第二部分仅与Fa(s)的区右极点（Re[s]≥β的极点）有关。

其实，计算式（28）的复变函数积分，还是非常困难的，下面假设Fa(s)是真分式，进一步研究式（28）的复变函数积分问题。

在s平面上，以s=0为圆心，作一半径为R的圆周CR，与路径σ=σ0±j∞(α＜σ0＜β)交于 A点和 C点，CABC（CADC）是CR上逆时针（顺时针）方向的一段弧，如图4所示。

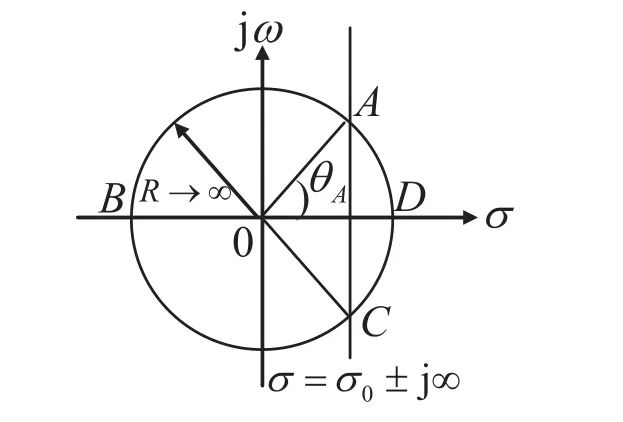
图4 s平面上围线积分路径示意图

令：

显然，式（30）满足围线积分引理条件，于是，有：

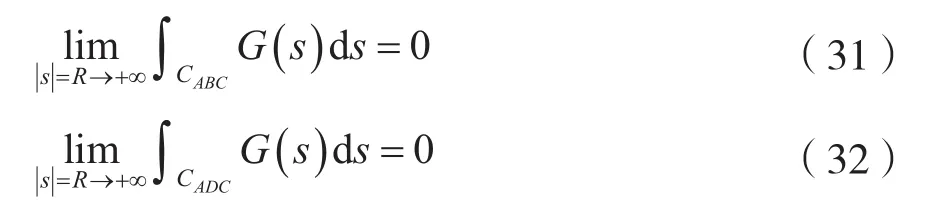
考虑到式（31）及式（32），则式（28）可写成：

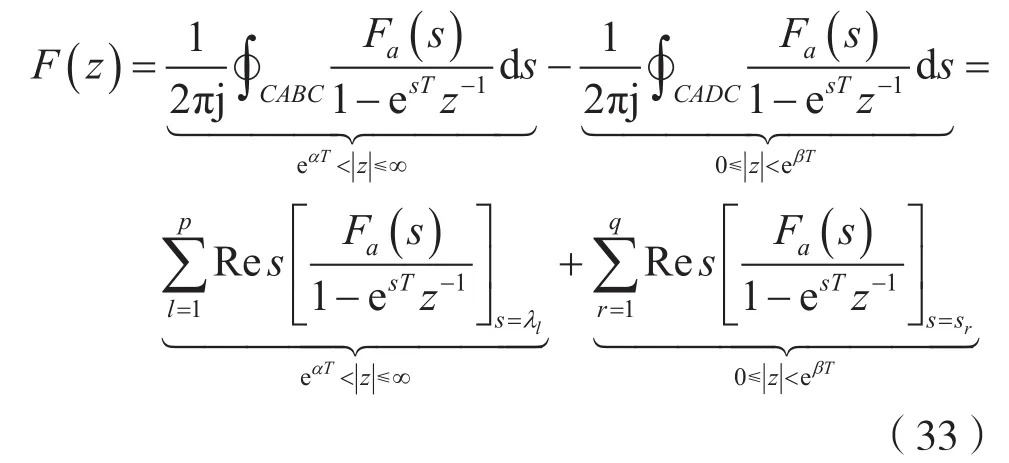
式中，s=λl(l=1,2,…,p)是Fa(s)的第l个区左极点（Re[λl]≤ α 的 极 点），s=sr(r=1,2,…,q)是 Fa(s)的第r个区右极点（Re[sr]≥β的极点）。

结论2：

式（33）揭示了一种直接利用连续信号的双边拉普拉斯变换来计算相应样值序列的双边z变换的方法。

讨论：

（1）设

考虑到式（6）及式（7），对式（34）两边取双边LT，可得：

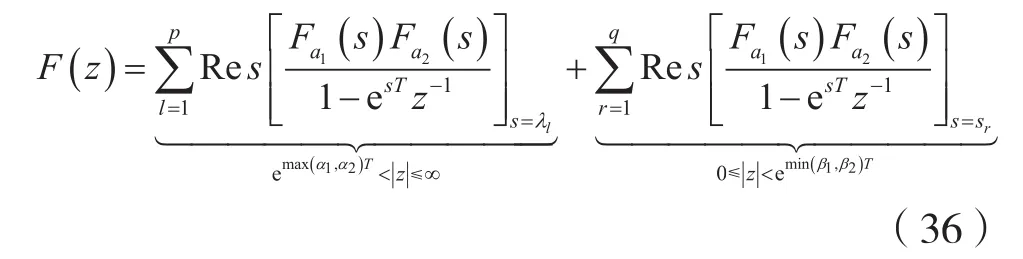
结论3：

式（36）揭示了一种直接利用两个连续信号各自的双边拉普拉斯变换来计算卷积信号相应样值序列的双边z变换的方法。

（2）设

考虑到式（8），对式（37）两边取双边LT，可得：

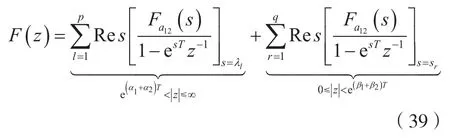
结论4：

式（39）揭示了一种直接利用两个连续信号各自的双边拉普拉斯变换来计算积信号相应样值序列的双边z变换的方法。

2.4 基于围线积分引理及留数定理计算Z域的卷积积分

由式（37）可知，对连续时间信号fa(t)抽样，其样值序列可写成：

积序列f(n)=f1(n)f2(n)的z变换除了利用式（39）进行计算外，还可用下述方法进行计算。

考虑到式（40）、式（20）、式（38）及式（8），则有：

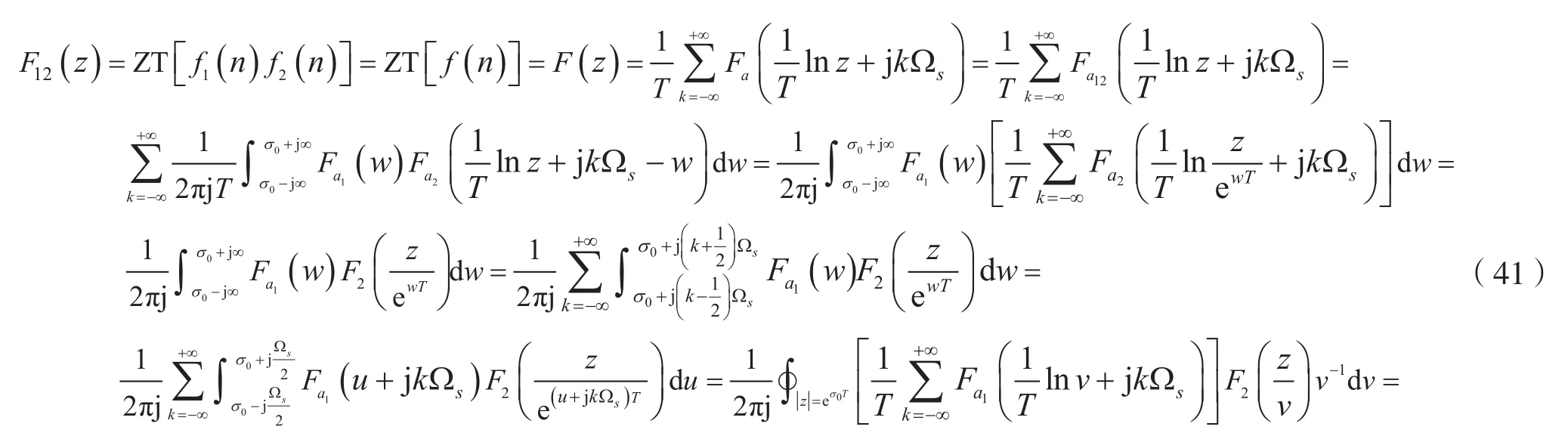
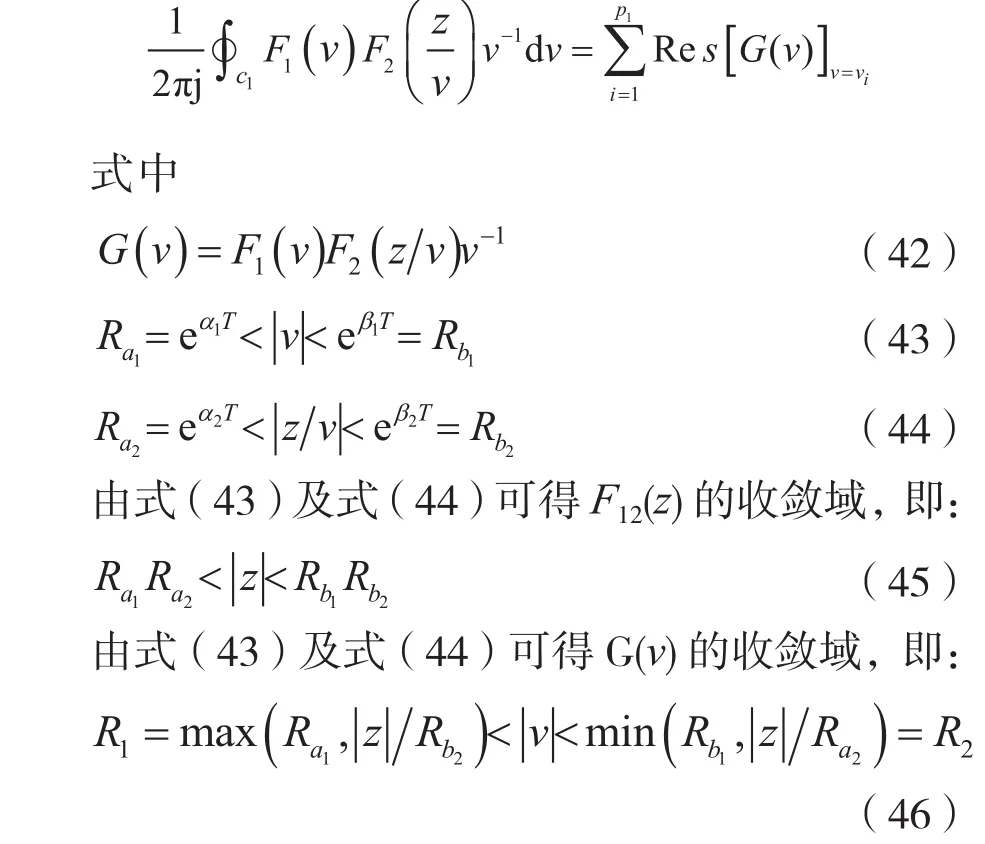
vi(i=1,2,…,p1)为G(v)在v平面上的区内极点，即|vi|≤max(va1,|z|/Rb2)的极点。

假设vj(j=1,2,…,p2)为G(v)在v平面上的区外极点，即的极点。为了利用G(v)的区外极点来计算F12(z)，先在v平面上G(v)的收敛区域R1＜|v|＜R2内画一条正向圆周曲线c1，再引入一条半径为无穷大的圆周曲线c2，最后选取一条将G(v)的所有区外极点vj均包括在内的积分路径，如图5所示。

图5 v平面上极点的围线积分路径示意图

若满足条件围线积分引理条件：

则有：

由图5可知，G(v)对区外极点vj(j=1,2,…,p2)作闭曲线积分时，沿闭曲线积分的路径由4段构成，它们分别是c1、c2、d1及d2。因为d1+d2线段的积分恒等于零，由式（48）可知，沿着c2的积分也恒等于零，于是，有：

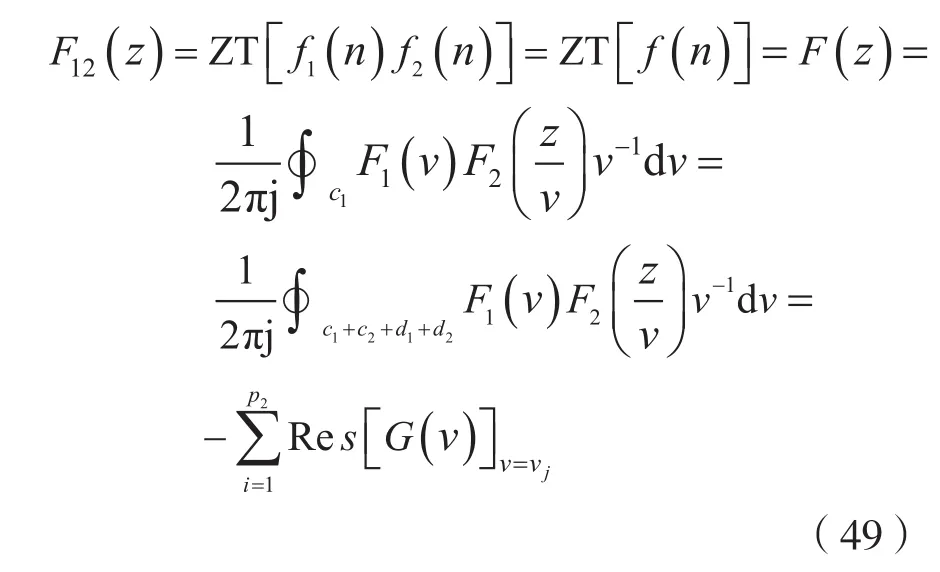
式中，G(v)=F1(v)F2(z/v)v-1，vj(j=1,2,…,p2)是 G(v)的区外极点，负号是由于围线绕行方向为负向（即顺时针方向）的缘故，F12(z)的收敛域仍为

当G(v)的区外极点数目较少时，适宜用式（49）进行计算，否则，适宜用式（41）进行计算。

例：设象函数

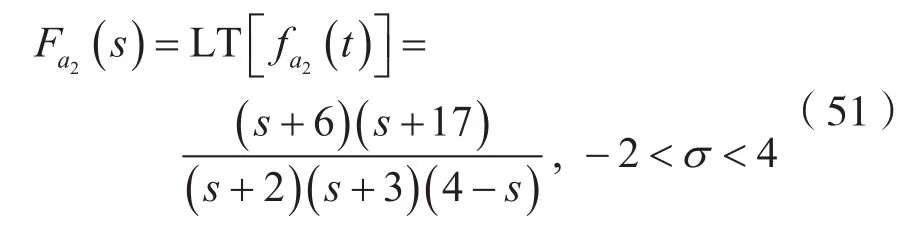
解：（1）考虑到式（50）及式（51），则有：

由式（57）及式（58）可知，G(w)有2个区左极点w=-1，w=s-4；有4个区右极点w=2，w=3，w=s+2，w=s+3，由式（12）可得：

（2）方法1：

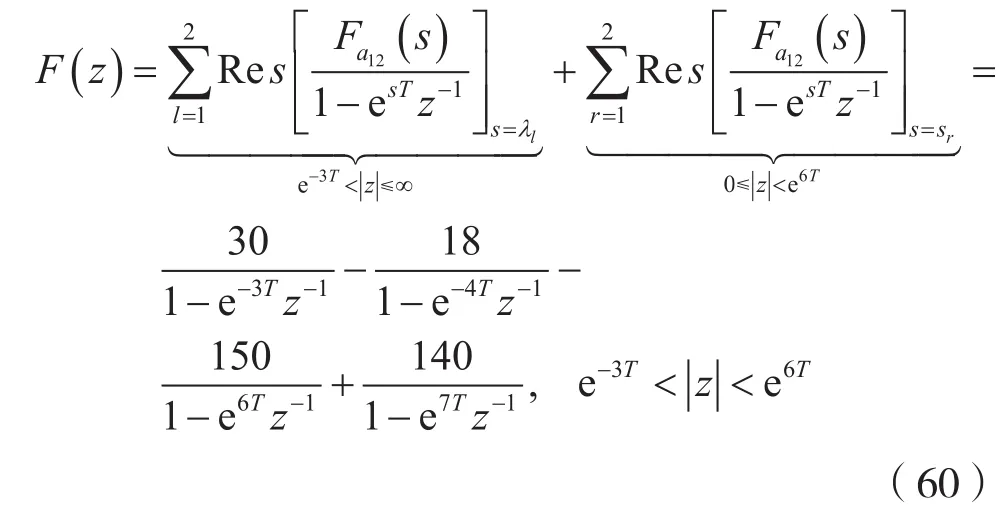
方法2：

由式（63）可得：

显然，式（64）满足围线引理条件。

由式（68）及式（69）可知，G(v)有2个区内极点v=e-T，v=e-4Tz；有4个区外极点v=e2T，v=e3T，v=e2Tz，v=e3Tz，由式（41）可得：

（3）考虑到

3 结 语

本文基于围线积分引理，给出了利用区左极点或右极点计算s域卷积的留数方法；依据连续时间非周期信号的拉普拉斯逆变换导出了非周期序列的逆z变换，基于围线积分引理，给出了利用区外极点计算有终序列的逆z变换及计算z域卷积的留数方法；提出了一种直接利用连续时间信号的双边拉普拉斯变换来计算相应样值序列的双边z变换的方法，并分别给出了利用两个连续信号各自的双边拉普拉斯变换来计算时域卷积信号及乘积信号相应样值序列的双边z变换的方法。