劳动年龄人口比例与地区住宅价格关系实证分析

李 昶（北京大学政府管理学院 北京 100871）

相关文献综述

住宅型房地产价格的形成与支撑机制、景气程度、市场周期一直是经济领域的研究热点。从需求端来看，根据Franco Modigliani的生命周期消费理论，个人可支配收入和财富的边际消费倾向取决于其年龄：人们在青壮年时期参与劳动借贷买房，在中年时期还贷同时为退休后储蓄（出售房产），在老年时期纯消费而无收入，用前期储蓄来弥补晚年消费，以实现整个生命周期内消费的最佳配置。因而一般认为劳动年龄人口（劳动年龄人口一般指法律规定的在一定年龄范围内具有劳动能力的人口。国际上一般将15-64岁列为劳动年龄人口，我国规定16-60周岁男性、16-55周岁女性为劳动年龄人口）是一国住宅型房地产的主要需求方，其规模、收入水平、风险偏好、预期等对房价走势有直接影响；而当人口老龄化，劳动人口占总人口比例下降，购房需求减少，退休人口出售房产用于养老，房价会下跌。

国内外研究中不乏从理论、实证视角论证人口年龄结构与住房价格相关关系的成果。Elod Takats（2010）基于22个发达经济体1970-2009年间的面板数据，证实了人口老龄化将使一国平均住宅价格下降；Robin Brooks（2014）则指出在资本市场最为活跃的经济体（澳大利亚、加拿大、新西兰、英国、美国等）中，资产价格尤其是房价并不会随着人口结构老龄化而呈现下降趋势，因为老年人口同样有财富积累动机；James Banks，Richard Blundell等（2010）则通过分析英美两国老年人口的住房换购行为，提出老年人口存在换购小面积、远离市中心的低价住宅行为，即老龄化抑制了住宅价格上涨；邹瑾（2014）基于系统广义矩阵估计讨论了人口老龄化对中国房价波动的长期影响，认为短期内人口老龄化对房价上涨有一定推动作用，但从中长期来看形势有所逆转；叶永刚、王凌伟等（2016）构建了包含人口年龄结构、预期房产收益率、利率的房价模型，利用1998-2011年中国省际面板数据进行验证，结果表明总抚养负担的下降是房价提升的重要推力；李祥、高波（2011）基于1995-2009年中国宏观数据发现，15-29岁、50-64岁人口比重与住宅消费及房价呈显著正相关关系；肖洋、宋旭（2014）的实证研究则表明人口年龄结构对房价的影响存在差异：老年抚养比在东部、西部、中部的影响依次减弱，少年抚养比在中部显示出较强影响力。

总而言之，现有关于人口年龄结构与住房价格关系的理论、实证分析大多忽略了样本数据的空间效应，或者仅对人口年龄结构、房价的空间异质性进行定性描述，鲜有从定量角度关注二者相关关系的空间依赖性。因此，本文拟从空间计量经济学的研究视角出发，运用2015年我国30个省级行政区的截面数据，探讨劳动年龄人口比例与地区住房价格之间的相关性。

我国省级行政区住宅价格的空间分布特征

本文首先将2005、2010、2015年作为考察年份，选取wind数据库中全国31个省级行政区相应年份的住宅年平均销售价格（单位：元/平方米）进行研究发现，从绝对数值来看，在省级层面，我国住宅价格水平大致呈现“西-中-东”梯度递增的不均衡分布状态；同时相邻省级行政区之间住宅价格水平相近，呈现出较为明显的空间集聚特征。从历年变化趋势来看，这一梯度分布状态较为稳定，2005-2015年未有大的变化，仅有部分地区（湖北、四川）在某些年份出现房价高地。

我国省级行政区住宅价格的空间相关性分析

（一）全局空间自相关测算

在GeoDa中，采用Rook一阶邻接空间权重矩阵对我国31个省级行政区2005、2010、2015年住宅价格进行全局空间自相关检验，得到相应年份的Global Moran's I指数（见图1）。从Moran's I数值来看，三个年份全局空间自相关指数均为正，且通过了1%水平的显著性检验，说明不同省级行政区住宅价格水平在空间上有相似属性，且呈现较强正相关性；从历年变化趋势来看，这种地理空间上的正相关性在逐渐减弱。

（二）局部空间自相关测算

进一步，利用局部空间自相关LISA指数描述各省级行政区与其周边地区在住宅价格上的差异程度，将Moran散点图转化为四象限图（见图2）。第一象限高高集聚（HH），表明中心省级行政区与周边地区住宅价格水平都较高；第二象限低高集聚（LH），表明中心省级行政区住宅价格水平较低，而邻近地区较高；第三象限低低集聚（LL），表明中心省级行政区及周边地区住宅价格水平都较低；第四象限高低集聚（HL），表明中心省级行政区住宅价格水平较高，而邻近地区较低。观察四象限可知，在考察的样本年份，北京、天津一直是中国住宅价格水平高地，而其周边中部省份住宅价格水平相对较低；云南及其周边地区则一直是住宅价格洼地，我国住宅价格水平呈现较为明显的两极分化特征。

劳动年龄人口比例与地区住宅价格的空间计量分析

（一）变量选取与数据来源

本文选取中国30个省级行政区（西藏地区数据暂不可得）2015年截面数据为样本，将住宅年平均销售价格P1（元／平方米）作为被解释变量，将各省级行政区年平均成交土地楼面价格P0（元／平方米）、经济发展水平L、少年抚养比Y（0-14岁少年儿童人口占15-64岁劳动年龄人口的比重）、老年抚养比O（65岁以上老龄人口占15-64岁劳动年龄人口的比重）作为四个解释变量，利用空间计量模型检验地区劳动年龄人口比例与住宅价格之间的相关关系。

本文所使用的各省级行政区年平均住宅销售价格、年平均土地成交楼面价格数据来自wind数据库；衡量经济发展水平的数据来自各省市统计年鉴；各省级行政区年龄结构数据来自《中国人口和就业统计年鉴2016》。在数据处理方面，为消除原数据异方差，对P1、P0作对数变换；经济增长水平L由各省级行政区2015年人均GDP收入（单位：元／人）的对数形式表示；少年抚养比Y=（0-14岁少年儿童人口／15-64岁劳动年龄人口）*100%，老年抚养比O=（65岁以上老龄人口／15-64岁劳动年龄人口）*100%，各省市数据处理结果如表1所示。

（二）空间计量模型设定及检验

首先，构建反映各省级行政区住宅价格与劳动年龄人口比例关系的计量回归模型，其表达式如下：

ln（P1）=α0+α1ln（P0）+α2L+α3Y+α4O+ε

然后，考虑到空间效应，分别构建省级行政区住宅价格的空间滞后模型（SLM）与空间误差模型（SEM），前者反映区域之间的溢出效应，后者则探讨由扰动误差项引起的空间依赖作用。空间滞后模型表达式为：

ln（P1）=α0+ρWln（P1）+α1ln（P0）+α2L+α3Y+α4O+ε

其中，W为空间权重矩阵，Wln（P1）为空间滞后变量，ρ为空间滞后回归系数，表征不同省级行政区之间溢出效应的程度。

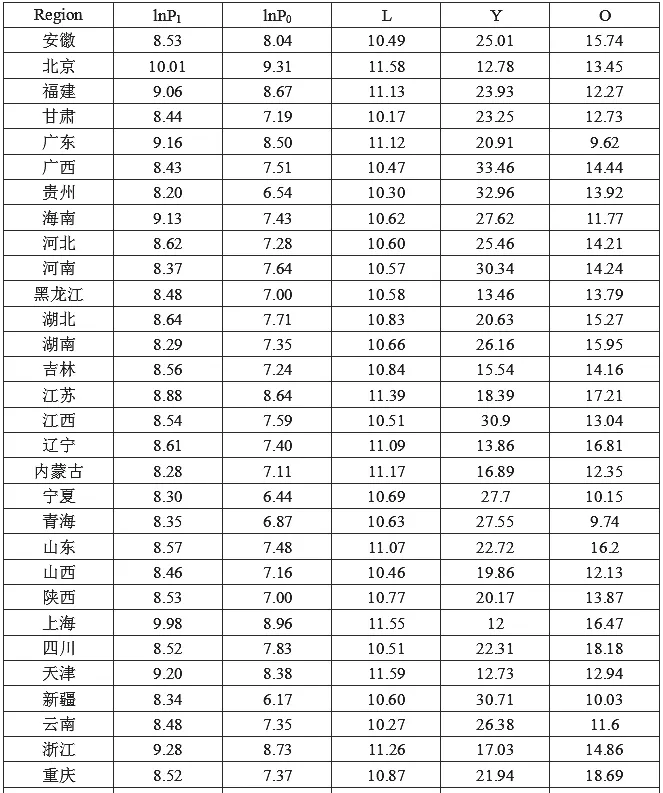
表1 各省市数据处理结果

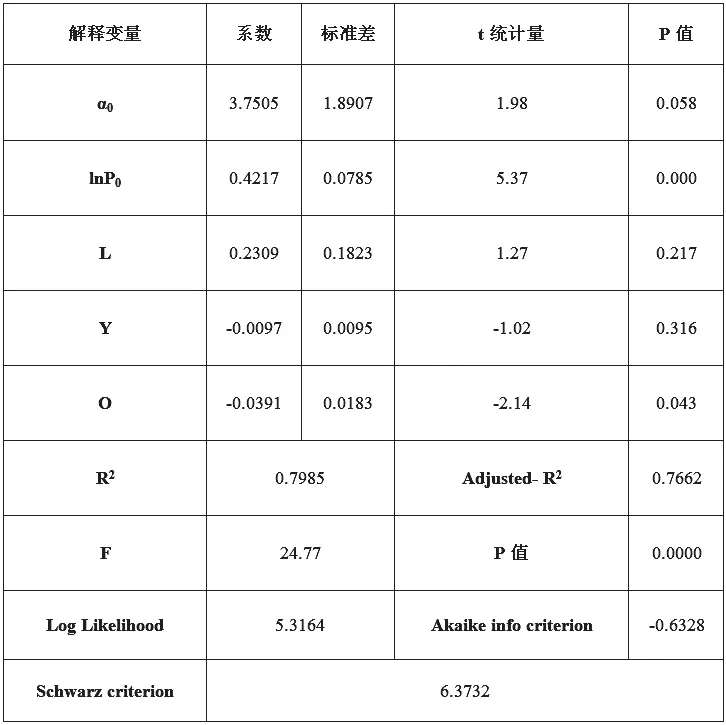
表2 劳动年龄人口比例与住宅价格的OLS估计

空间误差模型表达式为：

ln（P1）=α0+α1ln（P0）+α2L+α3Y+α4O+ε

ε=λWε+u

空间滞后模型只考虑了土地楼面价格、地区经济发展水平与少年抚养比、老年抚养比四个解释变量的影响，SEM则是基于“以上解释变量之外的误差项是空间相关”的假定设立的。上式中，λ表示空间误差自回归系数，Wε是空间滞后误差项，其余变量与SLM模型中相同。

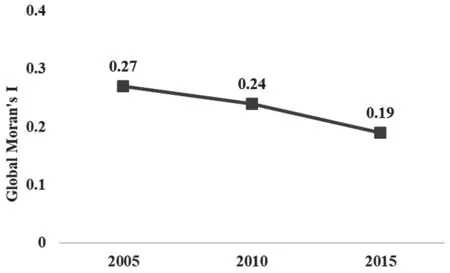
图1 2000、2005、2015年全国省级行政区住宅价格全局Moran's I指数

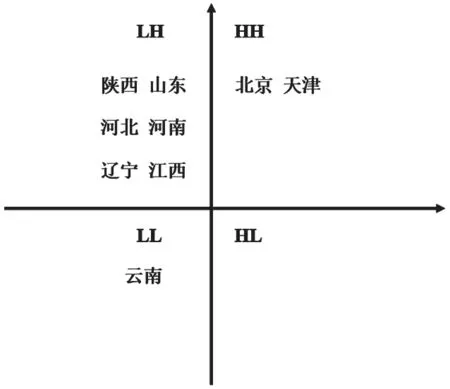
图2 2000、2005、2015年全国省级行政区住宅价格LISA指数

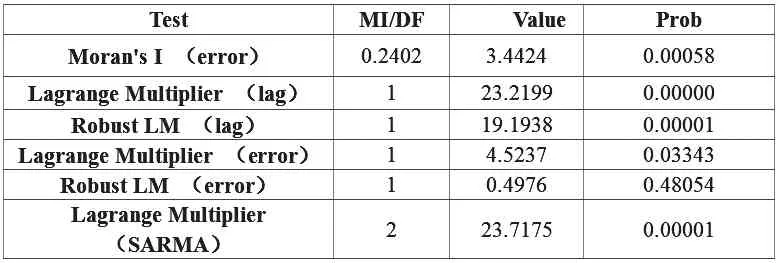
表3 空间依赖性检验结果

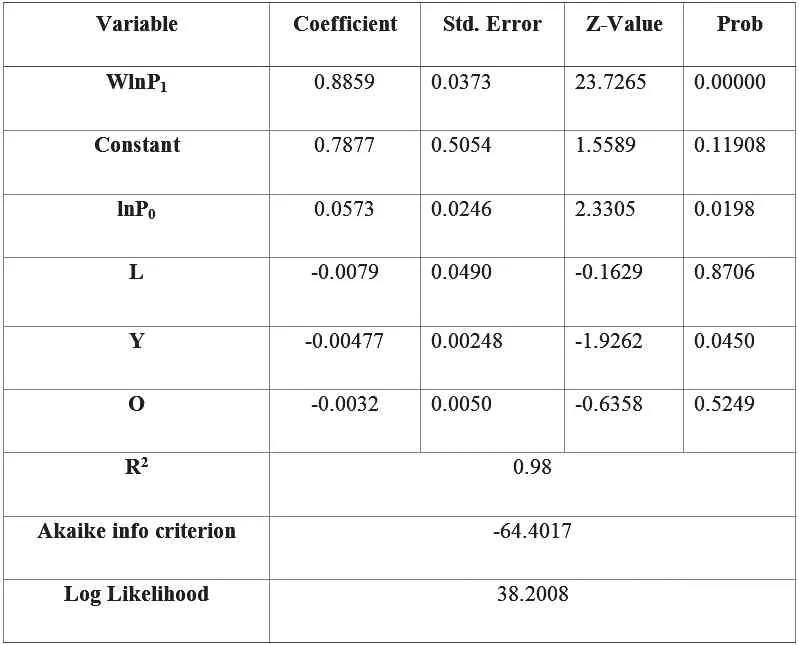
表4 劳动人口年龄结构与住宅价格的SLM估计

为比较SLM与SEM模型对于本文所研究问题的适用性，需对劳动年龄人口比例与住宅价格进行空间依赖性检验：若结果显示LM（Lag）相比于LM（error） 更为显著，同时Robust LM（Lag）显著而Robust LM（error）不显著，则选择SLM模型；若LM（error）相比于LM（Lag）更为显著，同时Robust LM（error）显著而Robust LM（Lag）不显著，则表明SEM模型对于本文所研究问题而言更佳。

（三）回归结果及分析

首先，根据前文构造的一般计量回归模型及整理后的数据进行OLS估计，结果如表2所示：模型F统计量为24.77，整体通过了1%水平的显著性检验；四个解释变量中土地楼面成交价格P0通过了1%水平的显著性检验，且估计系数为正，说明土地成交价对于住宅价格具有显著正效应，在不考虑其他因素影响的情况下，土地楼面成交价格每增长1%，该地区住宅价格将增长0.42%；老年抚养比O通过了5%水平的显著性检验，估计系数为负，即老年抚养比对于住宅价格有显著负效应，在不考虑其他因素影响的情况下，老年抚养比每增长1%，该地区住宅价格将下降0.04%；其余变量均未通过5%水平的显著性检验。模型拟合优度为0.7662，可以考虑引入空间因素改善OLS估计的偏差。

进一步利用GeoDa对OLS估计的残差进行空间依赖性检验，检验结果如表3所示。此处采用基于欧式距离的空间权重矩阵，结果显示，一般计量回归误差呈现明显的空间依赖性（通过1%水平的显著性检验）；此外，LM（lag）通过1%水平的显著性检验，而LM（error）未通过1%水平的显著性检验；R-LM（lag）通过了1%水平的显著性检验，R-LM（error）未通过10%水平的显著性检验。根据前文提到的模型选择标准，本文选用SLM空间计量模型更为合适。

继续利用GeoDa对设定的SLM模型参数进行估计，结果如表4所示：SLM模型整体拟合优度R2达到0.98，Log-Likelihood值38.2008，均优于OLS估计对应值；同时Akaike值也小于OLS估计值，说明空间滞后模型整体拟合优度好于一般计量回归模型。

具体而言，空间滞后变量WlnP1的空间自回归系数为正（0.8859），且通过了1%水平的显著性检验，说明各省级行政区住宅价格在空间上有较强溢出效应，即住宅价格涨跌可以通过邻近省级行政区之间传递。与OLS估计相比，四个解释变量中，年平均成交土地楼面价格lnP0与少年抚养比通过了5%水平的显著性检验。其中土地楼面价格对于住宅价格有显著正向影响，意味着土地价格（土地供需关系的反映）仍然是决定房价涨跌的关键因素，土地成交价格上升，房价也相应上涨；反之房价将下跌。而少年抚养比，即少年儿童人口占地区劳动年龄人口的比重对于住宅价格有显著负向影响，结合实际经验来看，少年儿童抚养负担的加重将使住宅主要需求方（15-64岁劳动年龄人口）可用于住宅消费、投资的可支配收入减少，需求萎缩，房价相应下跌；反之，当少年儿童抚养比负担减小，人们就有更多可支配收入用于住宅消费与投资。

结论

本文运用空间计量模型考察了我国30个省级行政区的劳动年龄人口比例与住宅价格之间的相互作用机制。在比较OLS估计与空间滞后模型估计结果的基础上，得出以下结论：

首先，我国各省级行政区住宅价格在空间上呈现出较强集聚性，并形成了“西-中-东”梯度递增的不均衡分布格局，这样的空间分布格局也保持着较为稳定的状态。其次，劳动年龄人口比例具体表现为少年人口抚养比，对于所在地区住宅价格具有显著负向影响，且这一影响具有较强空间溢出效用。即少年抚养比的上升，不仅使本省房价呈现下降趋势，还能通过空间传导机制对邻近省份住宅价格产生负向影响。这是由于少年抚养负担的加重使得劳动年龄人口可用于住宅消费、投资的可支配收入减少，导致住宅需求萎缩。最后，通过少年抚养比影响住宅价格的空间溢出效应呈现明显局部性特征，即其影响随着空间距离的增加而衰减，在地理空间上就表现为西、中、东部省份住宅价格水平呈现明显梯度分布。

未来研究展望

囿于笔者能力有限及数据可得性，本文在模型设置、数据选取方面仍存在一定不足，未来研究可从以下方面进行完善和拓展：

其一是在数据选择上，本文采用我国省级截面数据，样本量较少（30），模型回归结果稳健性不足，未来在精力允许的情况下可以考虑选用我国地级市或大中型城市某一时期内面板数据，扩大样本容量。

其二是在变量选择与设定上，本文纳入模型的解释变量（土地交易价格、地区经济发展水平、劳动年龄人口比例）较少，主要依据生命周期消费理论所涉及的住宅消费影响因素设置，并不能全面反映住宅价格形成机制，OLS估计和SLM估计中均有变量未通过显著性检验，说明模型整体解释力度仍存在较大优化空间；以少年抚养比、老年抚养比表征劳动年龄人口比例也只是一家之言，而这一比例可用多种指标量度（如15-64岁人口占总人口比重等）。

其三是在空间权重矩阵选择上，本文将GeoDa中自带的基于欧式距离的空间权重矩阵纳入模型，但并未就适用性与其它类型的空间权重矩阵（如Rook、Queen邻近矩阵）进行比较，主观因素较强，对回归结果的稳健性有一定影响。