基于长短期记忆神经网络模型的空气质量预测

张冬雯 赵琪 许云峰 刘滨

摘 要：隨着城市化和工业化的快速发展，空气污染问题日益突出，空气质量预测显得尤为重要。当前一些有代表性的研究对空气质量进行实时监测和预报，例如周广强等采用数值预报的方法对中国东部地区的空气质量进行分析，但其实验结果表明该方法难以预测非常重的污染;SANKAR等使用多元线性回归对空气质量进行预测，但其实验结果表明线性模型预测精度低、效率慢;PREZ等使用统计方法对空气质量进行预测，实验结果证明统计方法的预测精度比较低;WANG等采用改进的BP神经网络建立了空气质量指数的预测模型，其实验验证了BP神经网络收敛速度慢、容易陷入局部最优解的问题;YANG等利用相邻网格的空气质量浓度效应，建立了基于随机森林的PM2.5浓度预测模型，通过实验过程证明网格划分程序削弱了后续空气质量分析的质量和效率。这些方法都难以从时间角度建模，其中预测精度低是比较重要的问题。因为预测精度低可能会导致空气质量预测结果出现较大的误差。

针对空气质量研究中预测精度低的问题，提出了基于长短期记忆单元（long short-term memory，LSTM）的神经网络模型。该模型使用MAPE，RMSE，R，IA和MAE等指标来检测LSTM神经网络与对比模型的预测性能。由于Delhi和Houston是空气污染程度比较严重的城市，所以使用的实验数据集来自Delhi的Punjabi Bagh监测站2014—2016年的空气质量数据和Houston的Harris County监测站2010—2016年的空气质量数据。

LSTM神经网络与多元线性回归和回归模型（SVR）的比较结果表明，LSTM神经网络适应多个变量或多输入的时间序列预测问题，LSTM神经网络具有预测精度高、速度快和较强的鲁棒性等优点。

关键词：计算机神经网络;空气质量;长短期记忆单元;深度学习;多元线性回归;回归模型

中图分类号：TP389;O175.8   文献标识码：A   doi：10.7535/hbkd.2020yx01008

Abstract：With the rapid development of urbanization and industrialization， the problem of air pollution has become increas-ingly prominent， and air quality prediction is particularly important. Some representative studies currently monitor and forecast air quality in real time. For example， ZHOU Guangqiang et al. Used numerical prediction to analyze air quality in eastern China. However， experimental results show that this method is difficult to predict and is very important. SANKAR et al. Used multiple linear regression to predict air quality， but the experimental results showed that the linear model had low prediction accuracy and slow efficiency;PREZ et al. Used statistical methods to predict air quality， and the experimental results proved the prediction accuracy of the statistical method relatively low; WANG et al. Used an improved BP neural network to establish a prediction model for the air quality index， and their experiments verified that the BP neural network has a slow convergence rate and is prone to fall into the local optimal solution problem; YANG et al. Air quality concentration effect， a PM2.5 concentration prediction model based on random forests was established， and the empirical process proved that the meshing program weakened the quality and efficiency of subsequent air quality analysis; these methods are difficult to model from a time perspective， and the prediction accuracy is low is a more important issue. Because low prediction accuracy may lead to large errors in air quality prediction results.

In this paper， a neural network model based on long -term memory （LSTM） is proposed to solve the problem of low prediction accuracy in air quality research.MAPE， RMSE， R， IA and MAE were used to test the predictive performance of LSTM neural network and the comparison model.Since Delhi and Houston are cities with high levels of air pollution， the experimental data sets used in this paper were from the air quality data of Punjabi Bagh monitoring station in Delhi from 2014 to 2016 and the air quality data of Harris County monitoring station in Houston from 2010 to 2016.

RNN是一种非常强大的算法，可以对数据进行分类、聚类和预测，特别是时间序列和文本。RNN可以看作是一个在体系结构中添加了循环的MLP网络。在图1中，可以看到有一个输入层（包含x1，x2等节点）、一个隐藏层（包含h1，h2等节点）和一个输出层（包含y1，y2等节点），这类似于MLP体系结构。不同之处在于隐藏层的节点是相互连接的，在普通RNN中，节点按一个方向连接，这意味着h2依赖于h1，h3依赖于h2。隐藏层中的节点由隐藏层中的前一个节点决定[19]。

RNN公式可表示为ht=σ（wxhxt+whhht-1+bh），（1）式中：wxh是输入到隐层的矩阵参数;whh是隐层到隐层的矩阵参数; bh为隐层的偏置向量（bias）参数;σ可以为Sigmoid，tanh或者ReLU函数。

2.2 長短期记忆网络（LSTM，long short-term memory）

RNN神经网络在处理长时间序列时容易产生爆炸梯度[20]问题，其正确性往往较差。为了解决这一问题，LSTM首先被HOCHREITER等[21]引入，并成为一种成功的架构。LSTM神经网络是RNN神经网络结构的一种变体，其主要思想是引入一种自适应门控机制，其决定了LSTM单元保持先前状态的程度，并记住当前数据输入的提取特征。

3 实验数据与度量标准

3.1 数据的获取

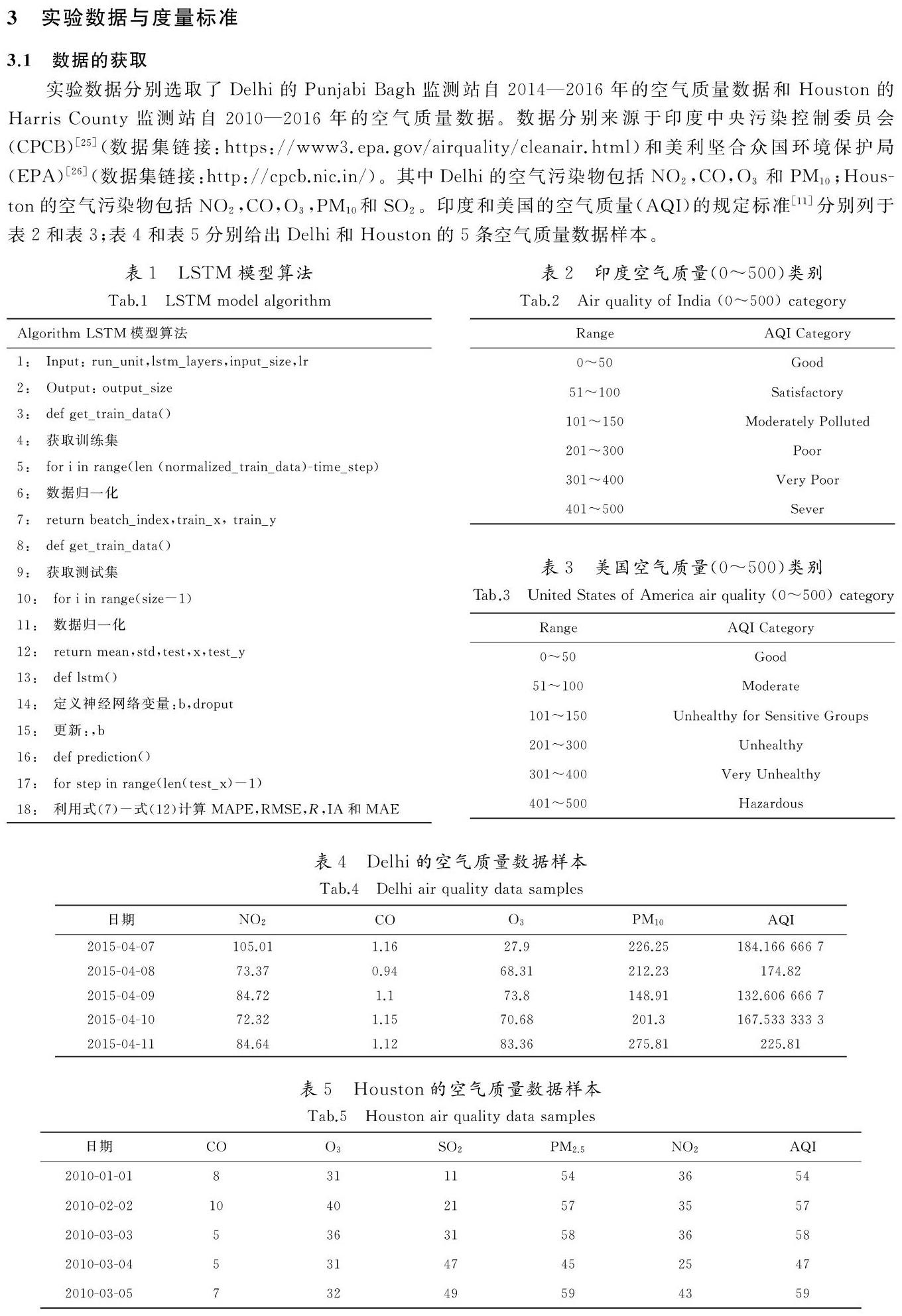
实验数据分别选取了Delhi的Punjabi Bagh监测站自2014—2016年的空气质量数据和Houston的Harris County监测站自2010—2016年的空气质量数据。数据分别来源于印度中央污染控制委员会（CPCB）[25]（数据集链接：https：//www3.epa.gov/airquality/cleanair.html）和美利坚合众国环境保护局（EPA）[26]（数据集链接：http：//cpcb.nic.in/）。其中Delhi的空气污染物包括NO2，CO，O3和PM10;Houston的空气污染物包括NO2，CO，O3，PM10和SO2。印度和美国的空气质量（AQI）的规定标准[11]分别列于表2和表3;表4和表5分别给出Delhi和Houston的5条空气质量数据样本。

3.2 空气质量数据的相关系数

本实验使用统计学中的皮尔森相关系数（pearson correlation coefficient，又称作PCCs或PPMCC，用R表示），分别在Houston和Delhi数据集上对AQI与各参数进行相关性分析，相关系数的绝对值越大，则表明X与Y相关度越高，如表6和表7所示。

为评价各回归模型的性能，选取了平均绝对误差（MAE）、平均绝对百分误差（MAPE）、相关系数（R）、均方根误差（RMSE）和一致性（IA）等统计指标，各指标皆由式（7）-式（12）给出。

1）MSE（mean squared error，均方误差）

均方误差是指参数的估计值与参数的真实值之差的平方的期望。MSE可以评价数据的变化程度，MSE越小，说明模型的拟合实验数据能力越强。SMSE=1n∑nk=1（tk-yk）2 。（7）  2） RMSE（root mean square error，均方根误差）

均方根误差是用来衡量观测值与真值之间的偏差。SRMSE=1n∑nk=1（tk-yk）2 。（8）  3） MAE（mean absolute error，平均绝对误差）

平均绝对误差能更好地反映预测值误差的实际情况。SMAE=1n∑nk=1|tk-yk| 。（9）  4） MAPE（mean absolute percentage error，平均绝对百分比误差）

平均绝对百分比误差常用来衡量历史误差。SMAPE=1n∑nk=1（tk-yk）yk×100% 。（10）  5） 相关系数（R）

相关系数用来衡量2个变量之间线性相关关系。R=∑nk=1（tk-）（yk-）∑nk=1（tk-）2∑nk=1（yk-）2 。（11）  6） IA（index of agreement，协议）SIA=1-∑nk=1（tk-yk）2∑nk=1（|tk-|+|yk-|）2 。（12）  其中n为数据点个数，yk为预测值，tk为观测值，为观测数据的平均值，为测试数据的平均值。SMAE，SMAPE，SRMSE的最小值和R，IA的最大值代表最佳模型。

4 实验和结果

4.1 实验设计

基于LSTM神经网络对数据进行划分：2014—2016年选出Delhi空气质量以460条数据为训练样本，对49条数据样本进行500轮;2010—2016年选出Houston以1 500条数据为训练样本，对500条数据样本进行500轮。其中实验设置隐藏层数为2层，当LSTM算法在Delhi和Houston数据集上分别选择学习率lr=0.000 9，lr=0.000 6时，效果最佳，该实验使用的Adam优化算法。

Delhi和Houston的空气质量预测的测试结果分别如图3和图4所示。

4.2 不同预测模型的性能对比

为了分析LSTM在空气质量预测的准确性，在本节实验中，将在Delhi和Houston的数据上使用LSTM算法和现有的一些方法进行对比，对比模型包括MLR（BGD），MLR（SGD），MLR（MBGD）和回归模型（SVR）。

本实验使用SMAPE，SRMSE，R，IA和SMAE作为模型对比的度量标准，表8和表9给出了Delhi和Houston两市所有模型的调查绩效指标。从2个表中可以看出LSTM模型的SMAPE，SRMSE和SMAE的值远远低于对比模型的SMAPE，SRMSE和SMAE的值，表8中MAPE降低了1.07%，RMSE减少了1.43，MAE减少了1.45;表9中MAE减少了4.26，MAPE降低了3.97%，RMSE减少了4.5;实验结果证明该方法是有效的。