降速工况下滚动轴承微弱故障特征信号提取新方法

栾孝驰，沙云东

（沈阳航空航天大学辽宁省航空推进系统先进测试技术重点实验室，辽宁 沈阳 110136）

1 引言

滚动轴承作为旋转机械重要的支承结构[1]，在其存在故障时直接影响到机械的正常运转。对于降速工况下，若直接对采集到的旋转机械振动信号进行傅里叶变换会造成严重的“频率模糊”的现象[2]。为此引入阶次分析的方法处理该类问题。阶次分析也称阶比分析，目前阶次分析主要分为两大类，一类是采用鉴相装置的硬件式阶次跟踪，另一类是计算阶次跟踪[3]。文献[4]分别利用鉴相装置和计算阶次跟踪这两种阶次分析方法对变速过程中旋转机械的故障进行诊断，且在采用高次插值时后者方法能够更加有效。文献[5]则重点研究以上两种方法混合形式的混合计算阶次跟踪技术，并结合多种插值方法，在旋转机械升速和降速过程中成功地诊断出多种转轴故障。文献[6]在计算阶次跟踪分析的基础上对时间进行离散以获得更加准确的重采样时刻。文献[7]对变工况齿轮故障特征进行了研究，通过实验仿真与验证说明了Hilbert解调与倒阶次谱相结合的方法对角域信号特征提取的有效性。文献[8]考虑到计算阶次跟踪的局限性而提出来基于匀角加速度方程的计算阶次跟踪技术并取得很好地效果。以上方法均未提及针对非稳态工况下轴承微弱故障的诊断方法。

提出了一种针对非稳态转速工况下微弱轴承故障特征信号的提取技术，即应用计算阶次分析、三次样条插值分析与包络谱分析相结合的新方法。基于滚动轴承模拟故障实验测得的降速工况下的转速信号和振动信号，首先对降速工况下的转速波形在时间域内积分获得角位移-时间曲线，再对角位移-时间曲线进行线性插值以获得角位移函数，对拟合函数求其反函数获得等角度间隔函数，然后利用该时间序列对振动信号进行三次样条差值获得等角度间隔分布的重采样振动信号，最后对重采样振动信号进行包络分析及快速傅里叶变换获得阶次包络谱。通过对滚动轴承微弱故障实验信号分析，表明该方法能有效提取出滚动轴承微弱外圈故障和滚动体故障特征信息。该方法为轴承微弱故障特征信号提取提供了一种重要手段，具有广泛的应用前景。

2 计算阶次重采样分析法

2.1 计算阶次跟踪技术

阶次分析基本目的和核心技术就是获得等角度间隔下的时刻以来对振动信号进行重采样。计算阶次跟踪技术常假定转速以匀变速变化，则转角θ可以利用2次函数来描述：

式中：b0、b1、b2—待定系数；t—时间。

在已知转轴转角增量Δφ的情况下，通过鉴相装置记录下所对应的三个时刻，从而可以确定未知系数b0，b1和b2。即：

将式（2）代入到转角函数可知：

在已知各个时刻后由式（3）可以求得｛bi｝，从而求得时刻值t，如式（4）所示。

对于求得的时间序列｛t｝对振动信号进行重采样再进行谱分析，从而获得阶次谱[4]。

从以上分析可知，计算阶次分析的核心是获得等角度间隔下的时间序列信号，通过该时间序列对振动信号进行重采样以获得阶次谱。为此提出了对转速信号进行处理以获得该时间序列的计算阶次分析技术。

2.2 三次样条插值

为了更好地对原始的振动信号进行重采样，在求得等角度间隔所对应的时间序列时对振动信号进行三次样条插值。三次样条插值的原理如下描述：

对于函数y=f（x），在区间［a，b］上一组节点a=x0＜x1＜x2＜…＜xn=b，就可以求得各个节点对应的函数值 y0，y1，…，yn，设 S（x）是函数y=f（x）的三次样条插值函数，则由插值函数的性质可知，S（x）在区间［a，b］上是二阶连续可微的，则可设 Mj=），j=1，2，…，n。根据三次样条函数的定义可知 S（x）在每一个小区间［xj，xj+1］上都是三次多项式，故）在区间［xj，xj+1］是线性函数，可表示为：

经过两次积分并利用 S（xj）=yj及 S（xj+1）=yj+1即可求得三次样条插值函数的表达式：

式中：j=1，2，…，n。

因此，结合样条插值的边界条件即可确定Mj和S（x），将插值节点代入后即可求得三次样条插值方法下的各个节点值[9]。

3 轴承故障特征阶次计算

3.1 轴承故障特征阶次计算理论

滚动轴承几何参数，如图1所示。图中：Db—滚动体直径；dm—内圈直径；Dm—外圈直径；Dc—节圆直径，且 2Dc=dm+Dm，θ—角接触角；z—滚动体个数。

图1 滚动轴承几何参数图Fig.1 Geometric Parameters of Rolling Bearing

当外圈固定时，轴承内圈、外圈和滚动体故障特征频率的计算公式为：

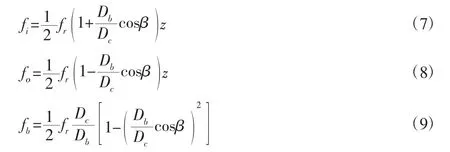
式中：fi、fo、fb—轴承内圈故障、外圈故障和滚动体故障的特征频率，单位为Hz；fr—参考轴转频。

阶次（Order）定义为参考轴每转内发生的循环振动次数，即O=循环振动次数/转。所以，当外圈固定时，轴承内圈、外圈和滚动体故障特征阶次的计算公式为：

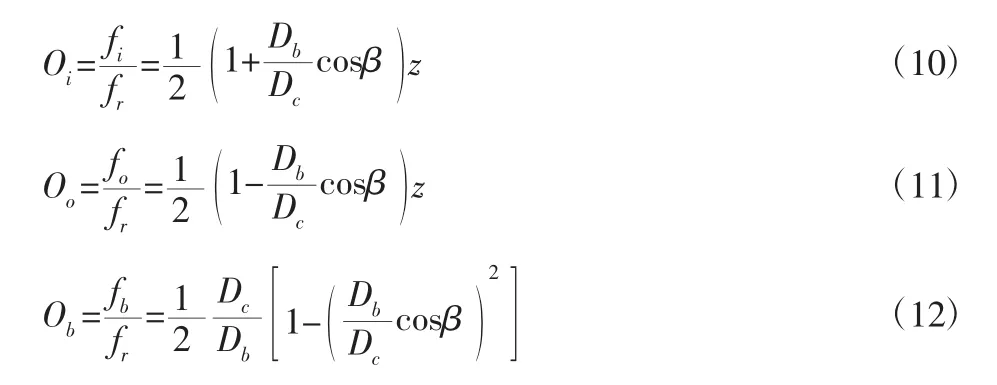
式中：Oi、Oo、Ob—轴承内圈故障特征阶次、外圈故障特征阶次和滚动体故障特征阶次。

3.2 阶次包络谱分析诊断流程

对现有的转速信号与振动信号分析可知，转速信号不是脉冲信号从而无法直接进行计算阶次分析。另可知转速信号和对应的时间序列，等时间间隔采样的振动信号序列和对应时间序列，通常振动序列的采样频率要远远高于转速序列采集速率，同时需要分析的最大阶次数为满足[10]：

基于计算阶次分析、三次样条插值分析与包络谱分析相结合的诊断分析步骤如下：

（1）对转速信号n（t）在时间序列｛t｝内进行数值积分获得等时间间隔的角位移序列θ0（t）；

（2）对所得到的角位移序列θ0（t）进行线性拟合并获得拟合函数θ＝f（t），拟合过程中的拟合误差为：

（3）以θ（t）序列的最小值和最大值为起点与终点，并设定插值长度 L，以来设定插值间隔角度：Δθ=（θ（t）max-θ（t）min）/L （15）

式中：Δδ—最小角度间隔。

以插值角度间隔进行插值，得到等角度间隔的角位移序列t′=f-1（θ′）及与其对应的新的时间序列｛t′｝；

（4）以获得新的时间序列｛t′｝对振动信号进行三次样条插值运算，获得重采样信号x′（t）；

（5）对重采样信号进行Hilbert变换和快速傅里叶变换，获得阶次包络谱；

（6）将得到的阶次包络谱和轴承故障特征阶次进行对比分析，提取出轴承微弱特征信息。

4 降速工况下滚动轴承特征信号提取技术

4.1 试验设备和试验轴承

滚动轴承试验的装置主要由变速电机、柔性联轴器、轴承座、转轴、安装轴承、试验轴承和转子等组成。数据采集系统为LMS SCADAIII，传感器为PCB加速度传感器，采用电涡流位移传感器测取转速信号。4个加速度传感器安装在试验轴承的轴承座上，1号传感器为垂直测点位置，2号传感器为轴向测点位置，3号和4号传感器为水平测点位置，滚动轴承故障试验台及传感器布置图，如图2所示。

图2 滚动轴承故障试验台及传感器布置图Fig.2 Rolling Bearing Fault Test Bed and Sensor Layout

4.2 滚动轴承特征信号提取技术

试验轴承型号为TMB-N204M，滚动轴承由z=11个，直径为Db=6mm的滚动组成，接触角β=0°，外圈直径为47mm，内圈直径20mm，节圆直径Dc＝33.5mm。外圈和滚动体采用线切割加工故障，模拟轴承划伤故障形式，加工故障尺寸为宽×深：（0.2×0.2）mm。将轴承几何参数带入式（11）和式（12）可知轴承外圈和滚动的特征阶次分别为Oo=4.51和Ob=2.7。

选取试验过程中某组（30～45）s的降速过程轴承转速信号和振动信号进行分析。降速过程转速波形，如图3（a）所示。对降速过程的转速信号在时域内积分，积分得到的原始角位移曲线，并对得到的时间-角位移曲线进行线性插值拟合，拟合后的函数曲线，如图 3（b）所示。

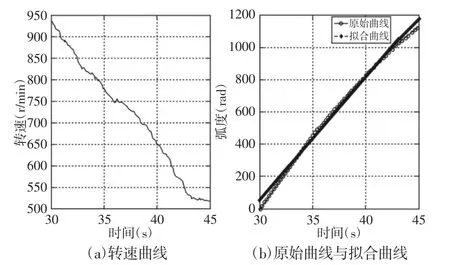
图3 轴承试验降速波形与拟合曲线Fig.3 The Velocity Waveform and the Angular Displacement Curve of Rolling Bearing Tests

试验过程中滚动轴承的振动信号采样频率fs=1024Hz。测试过程中垂直位置处传感器在降速过程中所采集到的振动信号时域波形及频谱，如图4所示。利用上述提出的技术方法，通过转速波形得到等角度间隔对应的时刻。由式（15）和式（16）计算可知插值角度间隔Δθ=0.0056rad，最小角度间隔Δδ=0.0084rad，显然满足角域重采样原则。故利用等角度间隔所对应的时间序列对振动信号进行三次样条插值的重采样处理，对处理后结果进行包络谱处理，得到重采样振动信号时域波形及阶次包络谱，如图5所示。

图4 垂直测点振动信号时域波形及频谱Fig.4 The Vibration Signal Time Domain Waveform and Spectrum of the Vertical Measurement Point

图5 垂直测点重采样振动信号时域波形及阶次包络谱Fig.5 Resampling Vibration Signal Time Domain Waveform and Order Envelope Spectrum of the Vertical Measurement Point

垂直测点原始振动信号降速时域波形，如图4（a）所示。信号直接进行频谱分析结果，如图4（b）所示。图中呈现出以15Hz为中心频率的一簇高的峰值，其他频带频谱峰值平缓，这是产生了“频率混叠”现象，不能体现出轴承的故障信息。垂直测点重采样振动信号的时域波形，如图5（a）所示。重采样振动信号的阶次包络谱分析结果，如图5（b）所示。图中出现明显的阶次峰值为1.34、2.67和4.65，阶次1.34为轴承的滚动体故障计算阶次Ob＝2.7的1/2，可知该阶次为轴承滚动体故障阶次的谐波成分，阶次2.67与轴承的滚动体故障计算阶次Ob＝2.7非常接近，阶次4.65与轴承的外圈故障计算阶次Oo＝4.51非常接近，分析结果表明该方法能够在降速过程中有效地提取出轴承滚动体故障和外圈故障特征阶次，进而可以有效识别轴承故障形式。

同理，对水平位置（测点3和4）测取的两路振动信号进行分析，阶次包络谱分析结果，如图6所示。从分析结果中可以看出，峰值阶次1.34和2.67在整个阶次谱中最为明显，而阶次4.63和4.56处存在较小的峰值。所以，水平位置振动信号阶次包络谱分析可以有效提取轴承滚动体故障特征阶次，对轴承外圈故障特征阶次提取不明显。

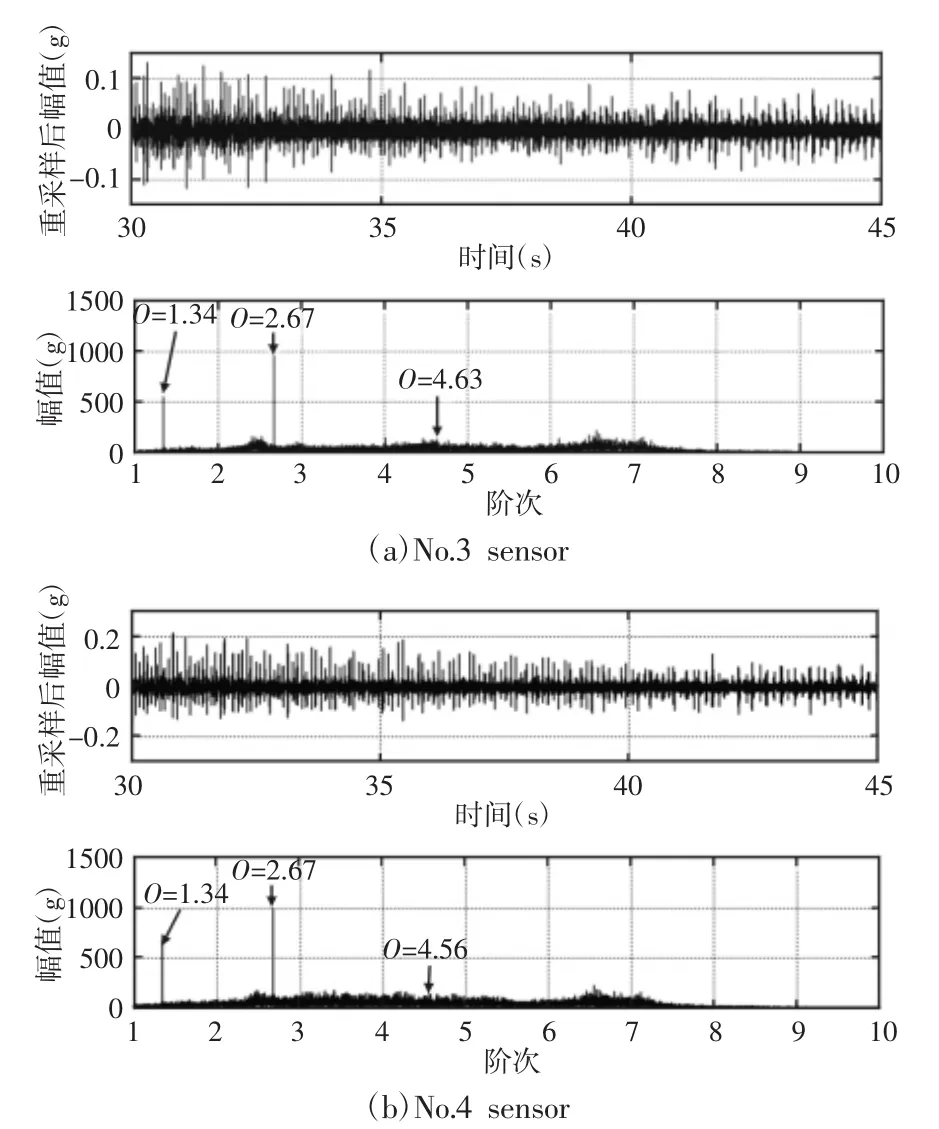
图6 水平测点重采样振动信号波形及阶次包络谱Fig.6 Resampling Vibration Signal Waveform and Order Envelope Spectrum of the Horizontal Measurement Point

综上分析可知，基于计算阶次分析、三次样条插值分析与包络谱分析相结合的方法可以有效地提取出轴承滚动体故障和外圈故障特征阶次，对轴承滚动体故障水平测点位置处识别效果好于垂直测点，轴承外圈故障垂直测点位置处识别效果明显好于水平测点。

5 结论

（1）提出的基于计算阶次分析、三次样条插值分析与包络谱分析相结合的方法，与传统阶次包络谱分析方法比较，最重要的是融合了三次样条插值分析原理，提高了角域重采样振动信号的准确性。（2）该方法以非平稳转速信号为基准，采用等角度采样技术和三次样条插值原理，将时域非平稳振动信号转化为角域平稳信号，该信号进行包络谱和FFT分析，获得轴承微弱故障信号特征。（3）通过对滚动轴承微弱故障实验振动信号分析，表明该方法能有效提取出滚动轴承微弱外圈故障和滚动体故障特征信息；测点位置不同诊断效果不同，对轴承滚动体故障水平测点位置处识别效果好于垂直测点，轴承外圈故障垂直测点位置处识别效果明显好于水平测点。该方法为轴承微弱故障特征信号提取提供了一种重要手段，具有广泛的应用前景。