模糊神经网络在汽车稳定性控制中的应用

唐 焱，赵宇鹏，蒋占四，肖蓬勃

（1.桂林电子科技大学机电工程学院，广西 桂林 541004；2.天津大学内燃机燃烧学国家重点实验室，天津 300072）

1 引言

随着道路条件的日益改善以及汽车性能的提高，车辆行驶速度也得到极大提升，因而如何提高高速车辆的行驶安全也逐渐成为国内外学者研究的重点。在高速车辆单车事故中，研究调查显示65%的高速车辆事故都是由于车辆侧滑造成的[1]。基于差动制动技术的车辆稳定性控制系统可以有效抑制车辆侧滑的发生，对于降低高速车辆的事故率，减少单车事故具有积极的意义[2]。

车辆动力学控制是个复杂的非线性问题。影响车辆行驶的环境因素复杂且实时多变，能够表征车辆状态的参数具有强烈的时变特性。基于模型的现代控制理论已经很难适应车载汽车电子稳定性控制系统（ESP）复杂的控制要求，因此自适应能力更强的智能控制算法成为应用趋势[3]。模糊控制被广泛应用于汽车电子控制系统中，虽然模糊逻辑能够有效处理复杂系统中的不确定性以及非线性问题，但是对于车辆运行状况的时变特性，模糊控制无法随车辆行驶条件的变化而自动修改适应，因而会影响控制的准确性[4]。考虑车速以及附着系数对车辆行驶稳定性的影响，设计了神经网络模糊控制器，有效提升了车辆稳定性控制系统对于复杂行驶工况的适应能力，达到了提高车载ESP系统控制精度和稳定性的目的。

2 车辆动力学模型及轮胎模型

车辆稳定性主要由横摆运动和侧向运动来表征，因此建立了七自由度车辆动力学模型。为实时模拟轮胎的力学特性则需建立准确的轮胎模型，采用“魔术公式”建立轮胎模型。

2.1 车辆动力学模型

七自由度车辆动力学模型，如图1所示。包括车辆纵向运动、侧向运动、横摆运动以及4个车轮的转动[5]。未考虑悬架结构，所以忽略车辆侧倾运动以及俯仰运动的影响，同时忽略空气阻力与滚动阻力。车辆纵向运动、侧向运动及横摆运动的动力学方程如下所示：

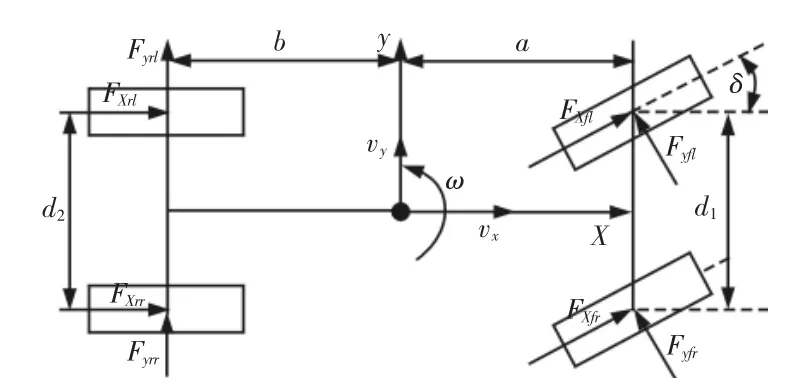
图1 七自由度车辆动力学模型Fig.1 Seven Degree of Freedom Vehicle Dynamics Model

纵向运动方程：

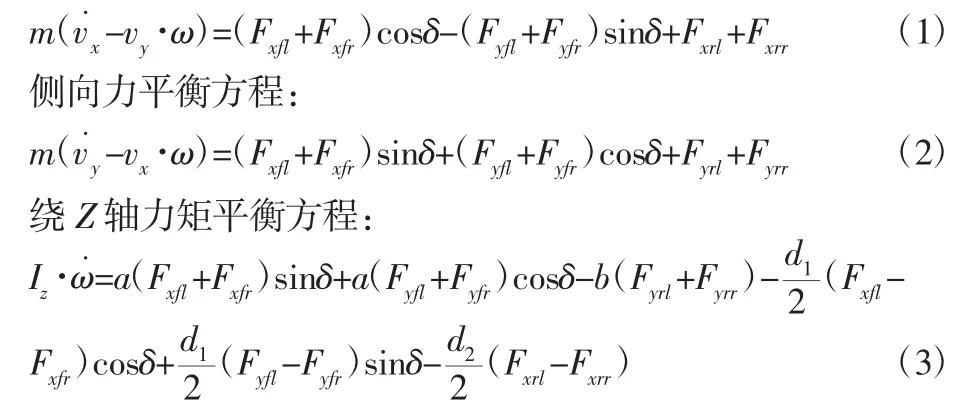
车轮转动方程：

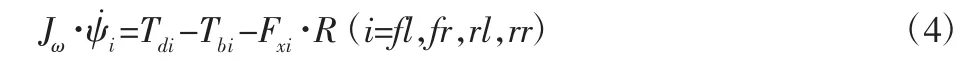
式中：m—整车质量；δ—前轮转向角；Fxfl、Fyfl—左前轮轮胎所受纵向力和侧向力；Fxfr、Fyfr—右前轮轮胎所受纵向力和侧向力；Fxrl、Fyrl—左后轮所受纵向力和侧向力；Fxrr、Fyrr—右后轮所受纵向力和侧向力；Tbi—各车轮制动力矩；vx、vy—车辆纵向速度和侧向速度；ω—横摆角速度；Iz—车辆绕z轴横摆转动惯量；a、b—车辆质心到前后轴的距离；d1、d2—前轮轮距和后轮轮距；Jω、ψ˙i、R—车轮转动惯量、车轮角加速度和车轮半径。

2.2 轮胎模型

为更好的模拟转向制动联合工况下的轮胎特性，采用Pacejka提出的“魔术公式”轮胎模型，忽略回正力矩的影响[6]，其在联合工况下的纵向力与侧向力其表达式如下：

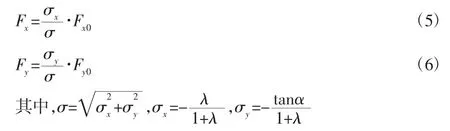
式中：Fx0—单一制动工况下的轮胎纵向力；Fy0—单一转向工况下的轮胎侧向力；σ—理想滑移率；σx、σy—理想滑移率的纵向和侧向分量。

虽然没有考虑车辆侧倾运动，但是由于车辆纵向与侧向加速度产生的动载荷会引起载荷转移，轮胎垂向载荷计算如下式：

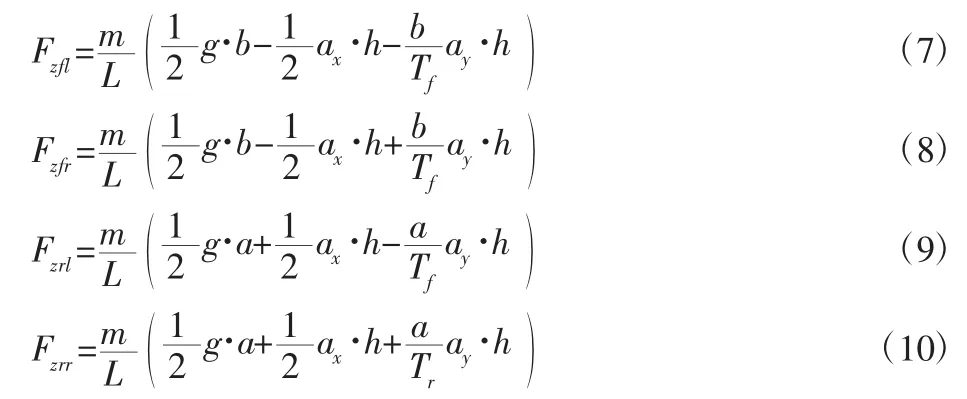
式中：Fzfl、Fzfr、Fzrl、Fzrr—左前轮、右前轮、左后轮和右后轮的垂向载荷；L—轴距（L=a+b）；ax、ay—车辆纵向加速度和侧向加速度；h—簧上质量的质心高度；Tf、Tr—前轮轮距和后轮轮距。

轮胎侧偏角和车轮滑移率是影响轮胎侧偏特性的两个重要因素，各车轮侧偏角的计算如下：

式中：α1—左前轮侧偏角；α2—右前轮侧偏角；α3—左后轮侧偏角；α4—右后轮侧偏角；fl—左前轮；fr—右前轮；rl—左后轮；rr—右后轮。

3 控制器设计

基于动力学控制设计的稳定性控制系统主要具有两类任务，即轨迹保持与稳定性控制，轨迹保持通常可由质心侧偏角描述，横摆角速度则可描述车辆稳定性，设计过程可将二者作为稳定性控制系统的控制变量[7]。控制系统设计原理结构，如图2所示。图中：Mz—上层运动控制器计算出的控制所需稳定横摆力矩，Tw—相应制动轮产生的制动力矩。分别比较实车与参考模型的质心侧偏角、横摆角速度，将两者偏差作为模糊神经网络（ANFIS）控制器输入量，即可根据偏差大小计算出控制所需的横摆力矩；再依据车辆行驶失稳条件判断，确定ESP系统是否介入，若介入即将上一层所计算出的控制所需横摆力矩传递给制动力分配系统，实现稳定性控制。

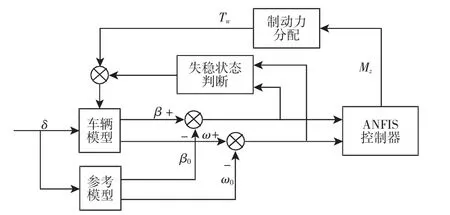
图2 稳定性控制系统结构示意图Fig.2 Stability Control System Structure Diagram

3.1 名义横摆角速度及质心侧偏角的确定

根据线性二自由度参考模型[8]可计算出名义质心侧偏角和横摆角速度，但考虑到路面附着系数的影响以及质心侧偏角物理极限值，名义横摆角速度和质心侧偏角的计算如下：

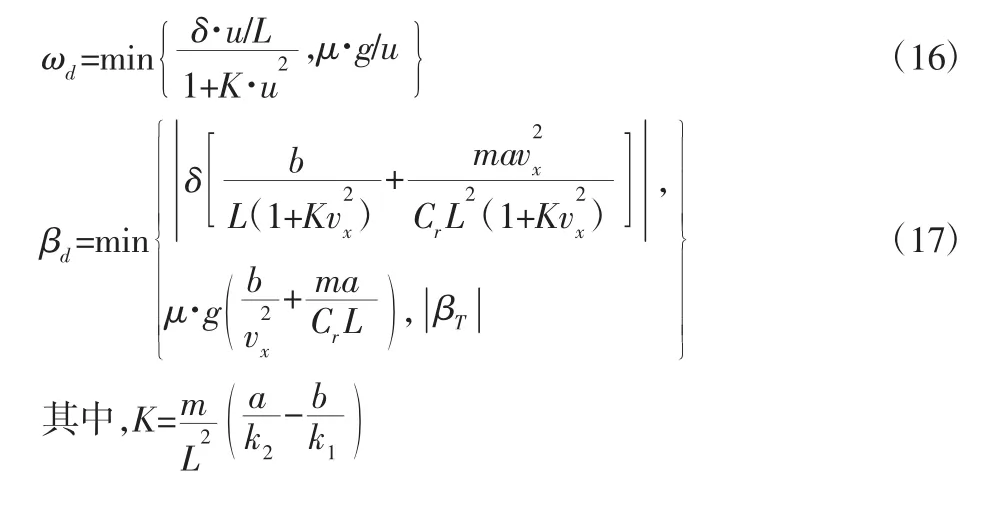
式中：βT—质心侧偏角的物理极限值，沥青路面为±12°，冰雪路面为±2°[9]。

3.2 模糊神经网络控制器设计

模糊神经网络控制是在模糊理论的基础上融合了神经网络学习机制，利用神经网络的学习能力修正模糊隶属度函数和控制规则，达到自适应的目的，具有更强的鲁棒性[10]。目前相关研究往往忽略复杂工况对系统控制精度的影响，尤其在复杂行驶工况（例如附着系数不均匀的路面）以及不同车辆行驶速度下的稳定性控制，常规模糊控制的控制精度则受其自适应能力制约。而模糊神经网络控制器，可以通过采集车辆在不同附着系数路面、不同行驶速度下的训练样本，以提高系统对复杂行驶工况的自适应能力。

3.2.1 自适应模糊神经推理系统

输入为质心侧偏角差值Δβ和横摆角速度差值Δw。自适应模糊神经推理系统，如图3所示。

第一层为模糊化层，确定输入变量的隶属度函数，选取Δβ和 Δw 的模糊论域均为｛NB，NM，NS，ZE，PS，PM，PB｝，其含义是｛负大，负中，负小，零，正小，正中，正大｝。隶属度函数采用三角隶属度函数。

第二层模糊规则强度释放层，将输入信号相乘，输出为每条规则的可信认程度，该层节点共有49个。

第三层归一化处理层，将所有规则进行归一化，方便计算。

第四层计算模糊规则的输出，该层节点均为自适应性节点。

第五层计算所有输入信号的总输出。

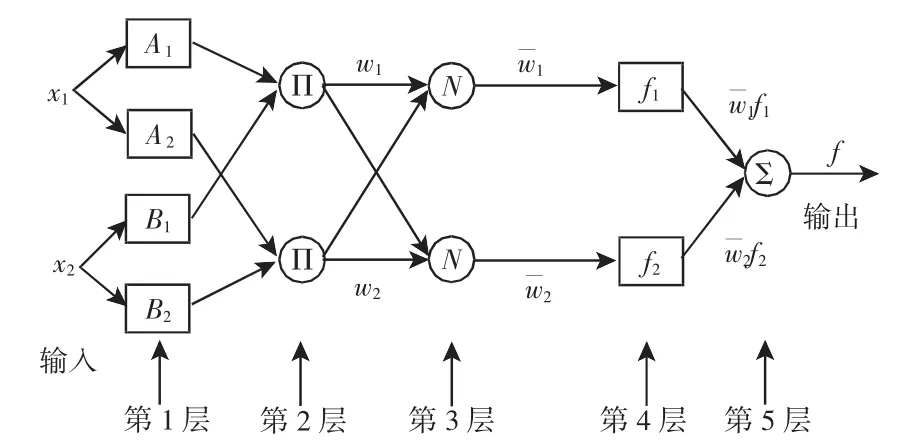
图3 自适应模糊神经推理系统Fig.3 Adaptive Neuro Fuzzy Inference System

3.2.2 训练数据

为了使模糊神经网络控制器能够适应多种车辆运行工况，利用车辆动力学仿真软件Carsim中“双移线”工况，考虑车速以及附着系数对车辆稳定性的影响因素设计了20组实验，用于采集训练所需的样本，具体实验方案，如表1所示。

表1 训练数据实验方案Tab.1 Selected Maneuvers for Training Data

3.3 制动力分配策略

在极限工况下，车辆稳定性控制不仅要求ESP系统准确的介入时机，同时要求制动分配系统能迅速响应，使各车轮获得合适制动力以产生足够强度的稳定横摆力矩满足控制需求。单侧车轮制动能够获得比单轮制动更大的制动力，产生的稳定横摆力矩更能满足控制系统快速性的要求，提高了系统控制效率，能够使车辆迅速恢复稳定行驶状态。这对于提升车辆极限行驶能力与安全性都至关重要。

假设极限工况下所有车轮未抱死，地面附着条件得以充分利用，前后轴车轮垂向载荷与制动力近似呈正比关系，且不考虑被动侧车轮侧向力的变化。以左侧车轮为例，前后轮可按下式进行分配：

则左侧制动产生的制动力矩为：

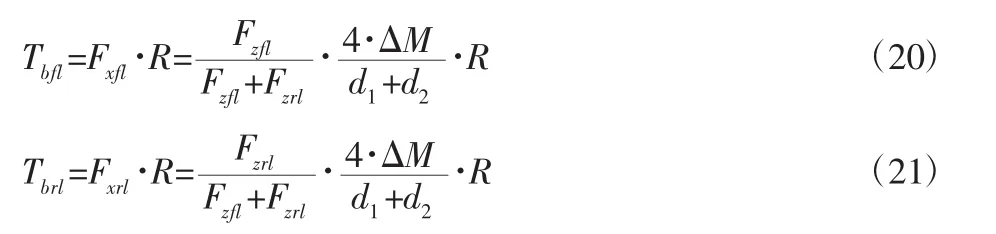
同理可得右侧制动产生的制动力矩为：

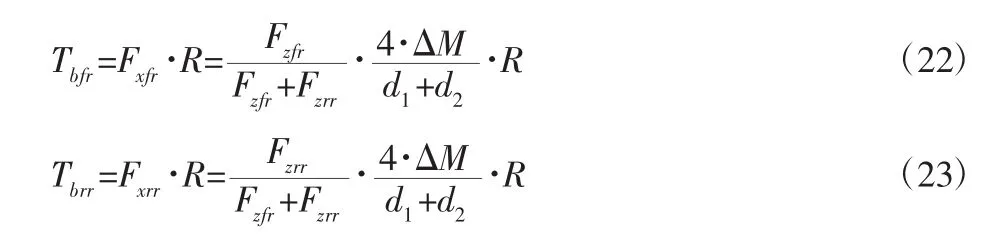
式中：ΔM—控制器计算出的平衡所需附加横摆力矩；R—车轮半径；Fzfl—左前轮垂向载荷；Fzrl—左后轮垂向载荷；Fzfr—右前轮垂向载荷；Fzrr—右后轮垂向载荷。

规定车辆左转转向角为正，横摆角速度逆时针为正，根据车辆运行状态分析以及差动制动控制原理，利用MATLAB/Stateflow有限状态机建立单侧制动制动轮选择逻辑，控制逻辑，如表2所示。

表2 制动轮控制逻辑Tab.2 The Control Logic of Brakeing Wheel

4 仿真结果分析

为验证控制策略的有效性，搭建了Carsim与Matlab/Simulink联合虚拟仿真平台进行仿真试验。在Carsim路面编辑器中采用插值法建立路面几何位置信息以及附着系数，附着系数变化范围从（0.5～0.8）。路面位置信息与附着系数关系，如图4所示。

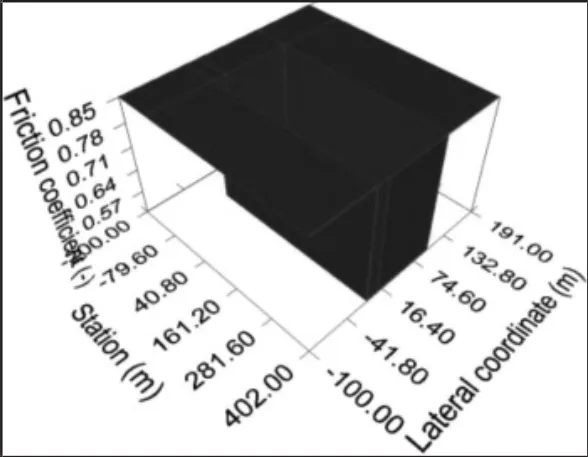
图4 路面位置与附着系数分布图Fig.4 Pavement Location and Adhesion Coefficient Distribution

仿真车型选取D级SUV，车辆参数为：a=1.09m，b=1.53m，d=1.44m，m=1764kg，Iz=2400kg·m2，Cf=64.5kN·m/rad，Cr=49.1kN·m/rad。车辆以120km/h的时速在附着系数分布不均的路面条件下进行双移线仿真实验，实验结果，如图5～图8所示。分析比较了模糊神经网络控制器与传统模糊控制器的控制效果，以及在有无搭载ESP系统控制下的车辆的瞬态响应。

车辆双移线工况前轮转向角输入，如图5所示。不同控制策略下车辆实际运行轨迹与预期运行轨迹的横向偏移量对比，如图6所示。由图6可知无ESP控制的车辆行驶路径发生了严重的偏移且车辆行驶出现失控，而有ESP控制的车辆行驶轨迹则能较好的跟踪目标路径，具有良好的轨迹保持能力。且显示搭载模糊神经网络控制器的ESP系统在等同条件下使车辆横向偏移量较常规的模糊控制更小，其控制精度更高，也更加平稳高效。

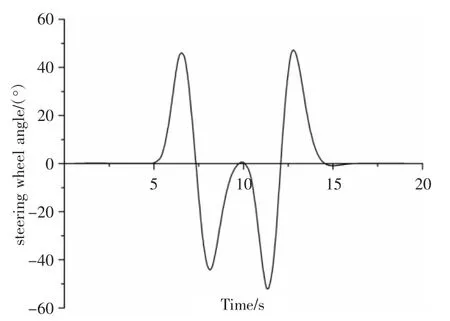
图5 方向盘转角输入Fig.5 Steering Wheel Angle Input

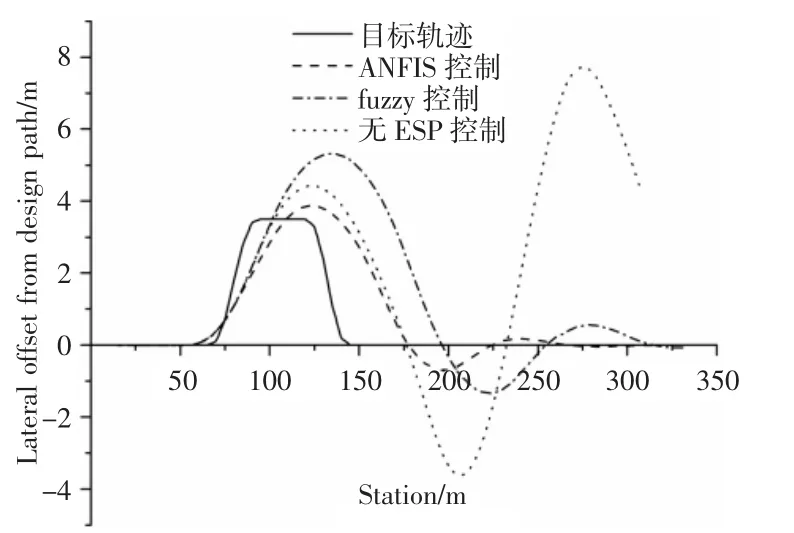
图6 对比设计路径的横向偏移量Fig.6 Lateral Offset from Design Path

双移线工况下不同控制策略下质心侧偏角随时间的响应变化曲线，如图7所示。双移线工况下不同控制策略下横摆角速度随时间的响应变化曲线，如图8所示。由图7、图8可见，搭载有有ESP控制系统的车辆，其横摆角速度与质心侧偏角均能被控制在名义值范围之内；而对比未加控制的车辆，其横摆角速度与质心侧偏角响应曲线随时间逐渐出现发散，显示车辆行驶已经失控。搭载模糊控制器的车辆，其横摆角速度在时间响应上相较于搭载模糊神经网络控制器（ANFIS）的车辆横摆角速度存在明显的滞后，大约在（0.3～0.4）s。质心侧偏角响应同样存在滞后性，但都保持在4°以内，显示车辆行驶保持在稳定区域。而且仿真结果显示搭载模糊神经网络控制器的车辆行驶达到稳态所需的调节时间更短，系统具有良好的动态性能。

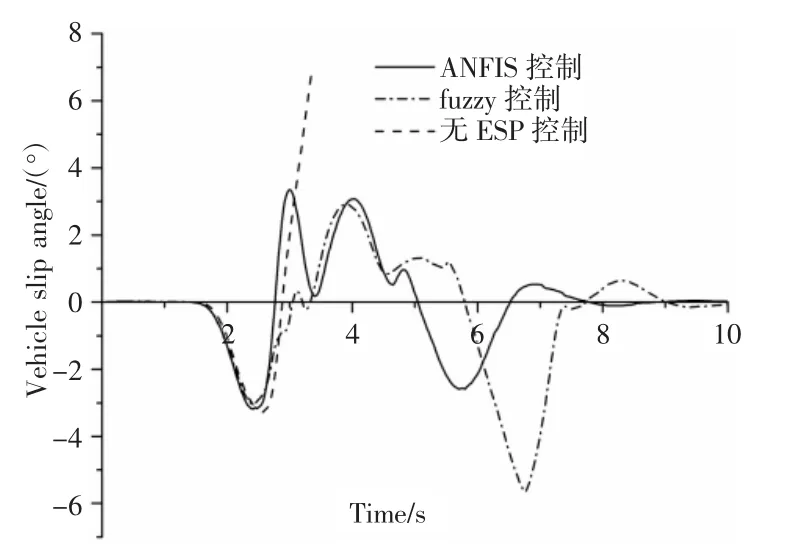
图7 质心侧偏角响应曲线Fig.7 Vehicle Slip Angle Response Curve

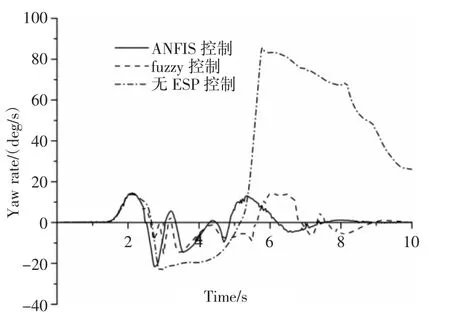
图8 横摆角速度响应曲线Fig.8 Yaw Rate Response Curve

5 结论

设计了基于模糊神经网络控制算法的车辆动态稳定性控制系统，并在Carsim与Matlab/Simulink环境联合仿真，结果表明：（1）在车辆高速行驶的情况下，采用所设计模糊神经网络控制器的车辆与采用常规模糊控制器的车辆相比具有更好的响应特性，车辆行驶具有更好的轨迹保持能力，且系统响应迅速。当轮胎侧偏力达到附着极限，车辆行驶进入非线性区域时，仍能使质心侧偏角与横摆角速度稳定在可控范围内，使车辆行驶更加稳定。（2）模糊神经网络控制器有效提高了车载ESP的动态特性，且更适应具有时变性、非线性的车辆动力学控制需求。