行星轮系中太阳轮断齿故障特性分析

史丽晨，李 坤，王海涛，刘 洋

（西安建筑科技大学机电工程学院，陕西 西安 710055）

1 引言

行星齿轮传动系统具有传动比大、承载能力强、体积小等诸多优点，广泛应用于风力发电、工程机械、直升机等领域[1]。由于其恶劣的工作环境，工作时常常发生轮齿故障，特别是断齿故障的发生造成整机工作不平稳甚至停机，从而造成难以估量的损失。因此对行星齿轮箱进行故障机理研究，并基于动力学建模来研究其故障特性至关重要。国内外目前对行星减速轮系的建模分析大多都是建立在正常状态下，缺乏对故障状态下的行星轮系建模研究[2-3]；对行星轮系进行故障特性分析时，缺乏振动机理方面的研究[4-5]；并且在对行星轮系建模分析时，没有考虑运行过程中振动传递路径时变效应的影响[6-7]。针对现有研究的不足，建立考虑振动传递路径时变效应的行星齿轮系统动力学模型，模型考虑齿轮副啮合综合误差、齿侧间隙等因素；推导太阳轮断齿故障下齿轮副的时变啮合刚度傅里叶级数表达式；通过对行星齿轮系统动力学模型的求解，分析得到太阳轮断齿时系统的频谱响应特性；最后通过试验信号进行对比，验证动力学模型分析结果的准确性。

2 行星轮系动力学建模

行星齿轮传动系统动力学模型，系统由太阳轮、行星架、内齿圈及 3 个行星轮组成，如图 1 所示。图中：θc、θs、θpi—行星架、太阳轮及各行星轮的自转角度；Kspi、Krpi、Cspi、Crpi—太阳轮和内齿圈与各行星轮的啮合刚度及啮合阻尼系数；2bspi、2brpi—啮合齿轮副侧隙；TD、TL—输入转矩和负载转矩。

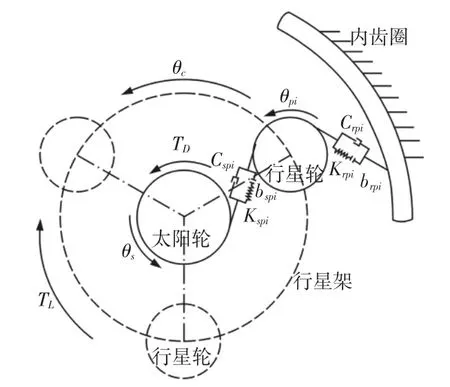
图1 行星齿轮传动系统动力学模型Fig.1 Dynamic Model of Planetary Transmission System

由Lagrange方程，可得图1所示动力学模型的微分方程：

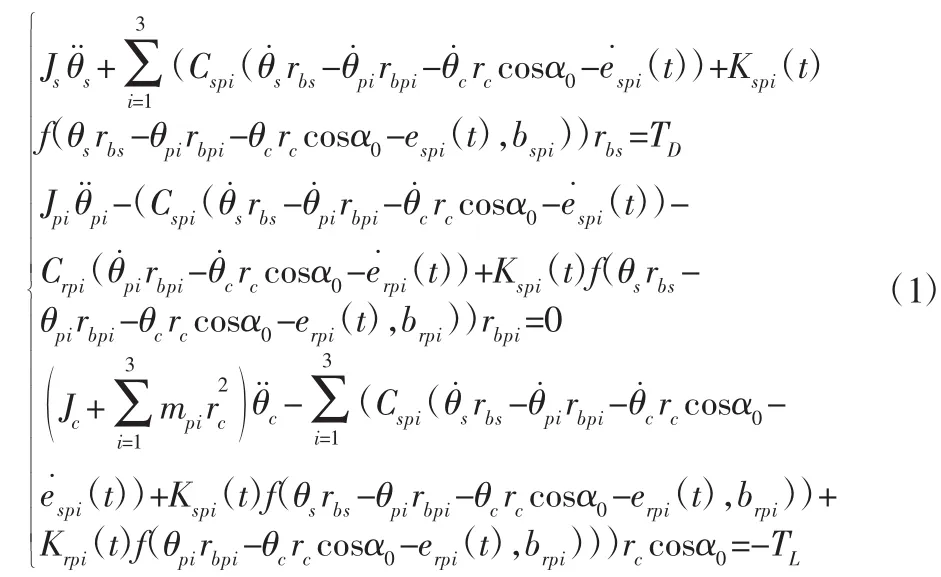
式中：Jpi—行星轮的转动惯量；Jc—行星架转动惯量；rbs—太阳轮基圆半径；rbpi—行星轮基圆半径；rc—行星架半径；mpi—行星轮质量；α0—压力角。

式中：espi（t）、erpi（t）—各齿轮副的综合啮合误差；f（x，b）—间隙非线性函数。为了便于求解，引入相对位移坐标：

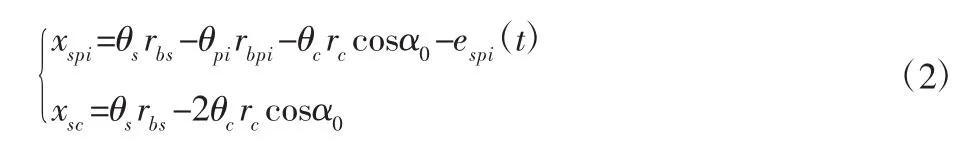
定义时间标称尺度ωn及位移标称尺度bc，得量纲一动力学微分方程为：

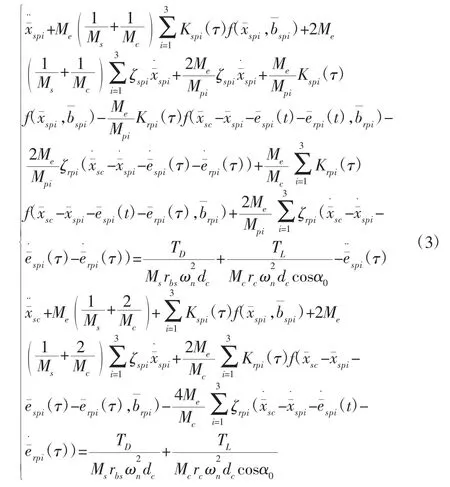
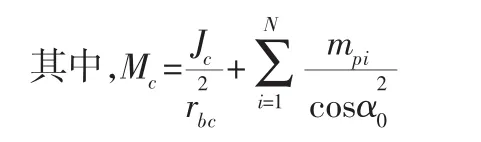
式中：rbc—行星架当量半径；

ζspi—行星轮i与太阳轮的啮合阻尼比；

ζrpi—行星轮i与内齿圈的啮合阻尼比；

Ms、Mp—太阳轮、行星轮在各自基圆半径上的等效质量。

在测量行星齿轮箱振动信号时，传感器一般固装在与内齿圈相连的箱体上，因此行星轮的公转会对测试信号产生调幅作用，这种调制作用称之为振动传递路径时变效应[8]。振动传递路径时变效应可用基频为行星架旋转频率fc的汉宁窗函数表示[9]，即在模型响应信号中引入传递路径函数C（t）：

3 太阳轮断齿故障啮合刚度表示

当齿轮发生断齿故障时，故障齿处刚度会减弱，其他齿处刚度不变。以傅里叶级数来表示齿轮副时变啮合刚度，先推导单对齿轮系统啮合刚度表达式，然后推广到行星齿轮传动系统中，得到太阳轮断齿时各啮合副的时变刚度表达式。

3.1 单对齿轮系统断齿故障啮合刚度表示

正常状态下齿轮副啮合刚度曲线，T为啮合周期，ka为刚度变化峰峰值，kav为平均啮合刚度，如图2所示。

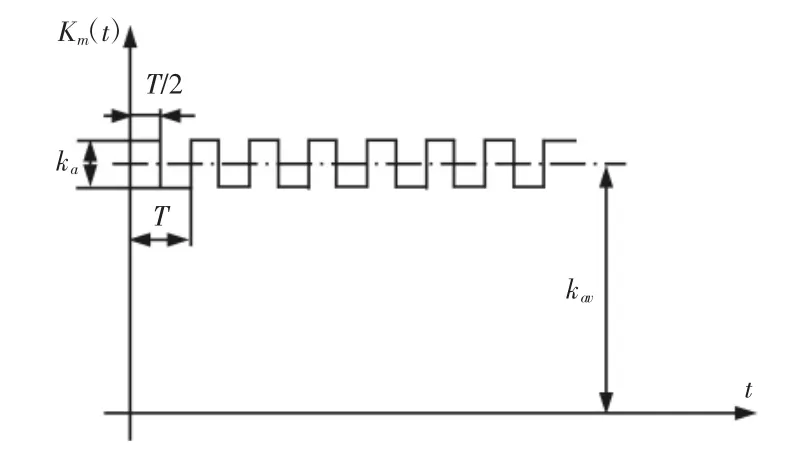
图2 正常齿轮啮合刚度曲线Fig.2 Gear Pairs Meshing Stiffness Curve Under Healthy Condition

由图2可得正常状态下的啮合刚度傅里叶级数表达式为：

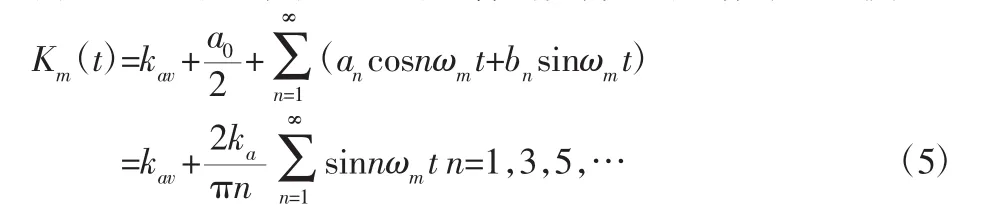
设单对齿轮系统某个齿轮有z个齿，其中一个齿发生断齿故障，啮合刚度曲线，如图3所示。其中，T1—故障齿轮旋转周期；kav1—断齿状态下的平均啮合刚度。

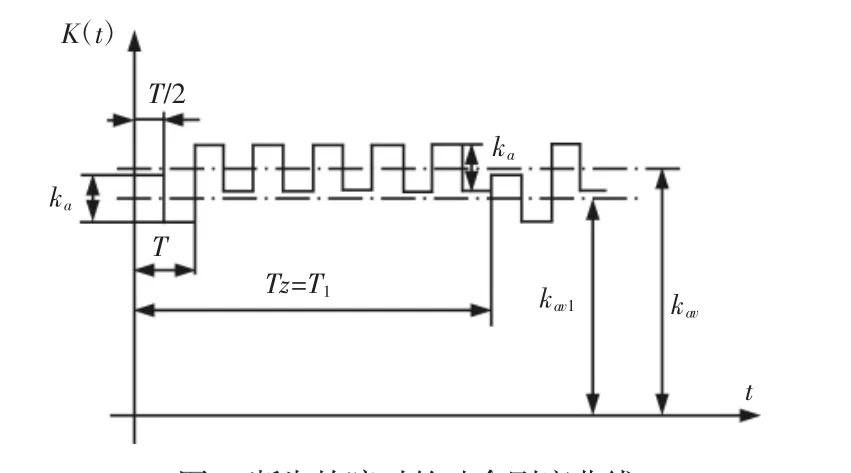
图3断齿故障时的啮合刚度曲线Fig.3 Gear Pairs Meshing Stiffness Curve Under Tooth Broken Condition

图2 和图3做差可得图4，即为断齿处啮合刚度的峰峰值图，如图4所示。

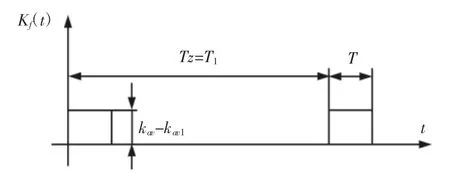
图4 断齿处啮合刚度变化的峰峰值图Fig.4 Peak-to-Peak Value Curve of Meshing Stiffness at Broken Tooth

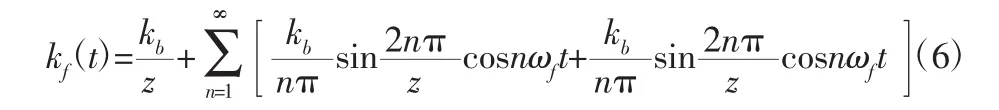
故可得图3的傅里叶级数表达式，即断齿故障下齿轮副的时变啮合刚度表达式为：

令kav-kav1=kb，则图4用傅里叶级数可表示为：

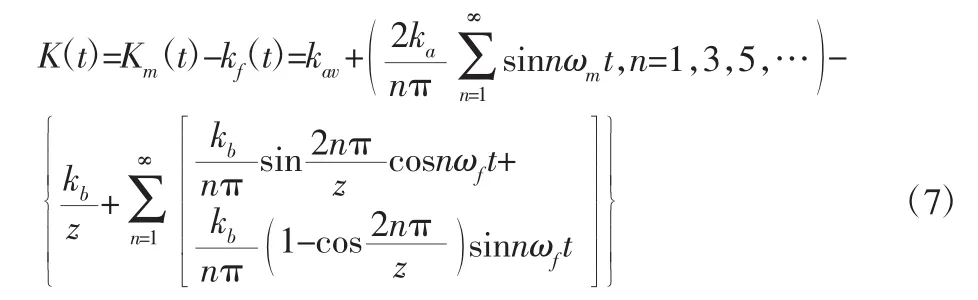
3.2 行星轮系太阳轮断齿故障啮合刚度表示

在行星齿轮箱中，内齿圈、太阳轮分别与3个行星轮啮合，共有 6 组啮合对，故对应 6 组啮合刚度[10]，即 Ksp1，Ksp2，Ksp3，Krp1，Krp2，Krp3。设三个行星轮均匀承载，具有相同的物理、几何参数，则正常状态下各齿轮副的啮合刚度表达式均，如式（7）所示。

设行星齿轮箱中太阳轮的某个轮齿发生断齿故障，则6组啮合刚度中Ksp1，Ksp2，Ksp3减弱，其余三种啮合刚度不变。此时Ksp1，Ksp2，Ksp3的峰峰值，如图 5 所示。

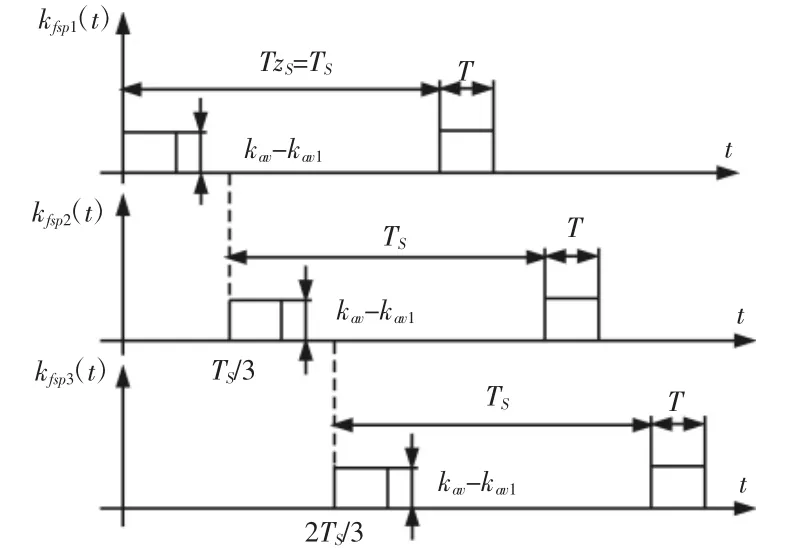
图5 太阳轮断齿故障时啮合刚度Ksp1，Ksp2，Ksp3的峰峰值Fig.5 Peak-to-Peak Value Curve of Meshing Stiffness Ksp1，Ksp2，Ksp3at Broken Tooth of Sun Gear

图中：kfsp1（t），kfsp2（t），kfsp3（t）—断齿啮合刚度Ksp1，Ksp2，Ksp3的峰峰值；zs—太阳轮轮齿数；Ts—太阳轮故障周期。

由式（6），得kfsp1（t）=kf（t），则：

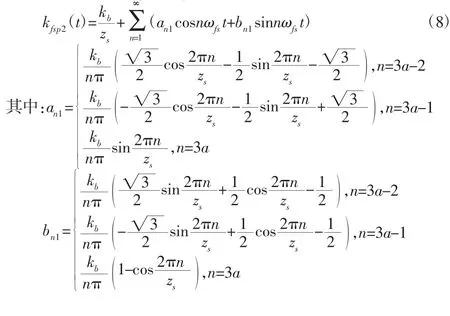
式中：a=1，2，3，…

因此太阳轮断齿故障下，各组啮合刚度的表达式为：

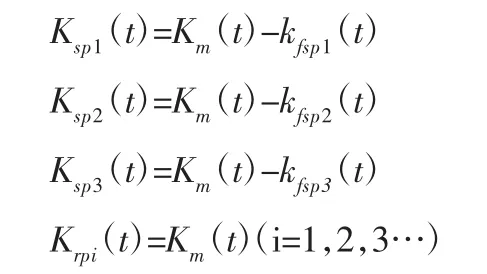
4 模型响应分析与试验验证

行星齿轮系统动力学模型的参数设置，如表1所示。

表1 行星齿轮箱参数Tab.1 Planetary Gearbox Configuration Parameters

将表1中的参数与求得的齿轮时变啮合刚度代入动力学模型中，求解得到模型响应信号，经传递路径函数调幅得到最终的模型响应信号，并对该信号作进一步分析，得到行星轮系的模型响应特性。

4.1 模型响应分析

通过动力学仿真，太阳轮断齿故障下模型响应的频谱图，如图6（a）所示。啮合频率附近局部放大的频谱图，如图6（b）所示。

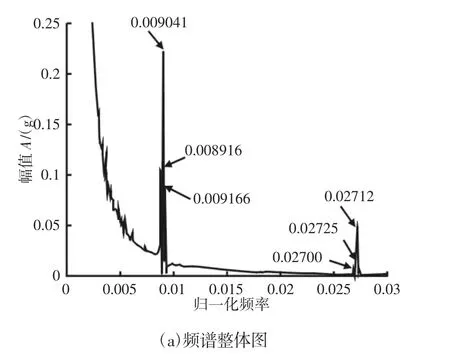
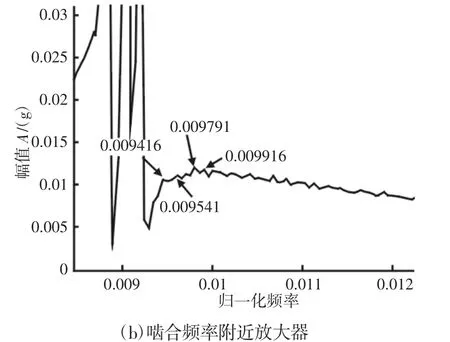
图6 太阳轮断齿时的模型振动响应频谱图Fig.6 Spectrum of Model Vibration Response for Sun Gear Broken

由图6可知，太阳轮发生断齿故障时，由于行星轮公转的调幅效应，频谱图中会出现调制频率为行星架转频的边频带，即处幅值较明显（k，n均为整数），如在归一化频率约0.009041）约0.008916）约0.009166）处的峰值较大。同时频谱中还出现了以太阳轮故障频率为调制频率的边频，如在归一化频率约0.009416）约0.009541）约0.009791）约0.009916）处边带峰值较明显，即频谱图中的幅值出现在归一化频率处（k，m，n均为整数）。

4.2 试验验证

为了验证所建立动力学模型分析结果的准确性，使用的行星齿轮箱故障诊断试验台进行试验验证，如图7所示。行星齿轮箱的参数与表1中的模型参数一致，信号的采样频率为20.48kHz。试验测得的太阳轮断齿故障下响应信号的频谱图，如图8所示。试验实际啮合频率约为216Hz。

图7 行星齿轮箱故障诊断试验台Fig.7 Planetary Gearbox Fault Diagnosis Test Rig

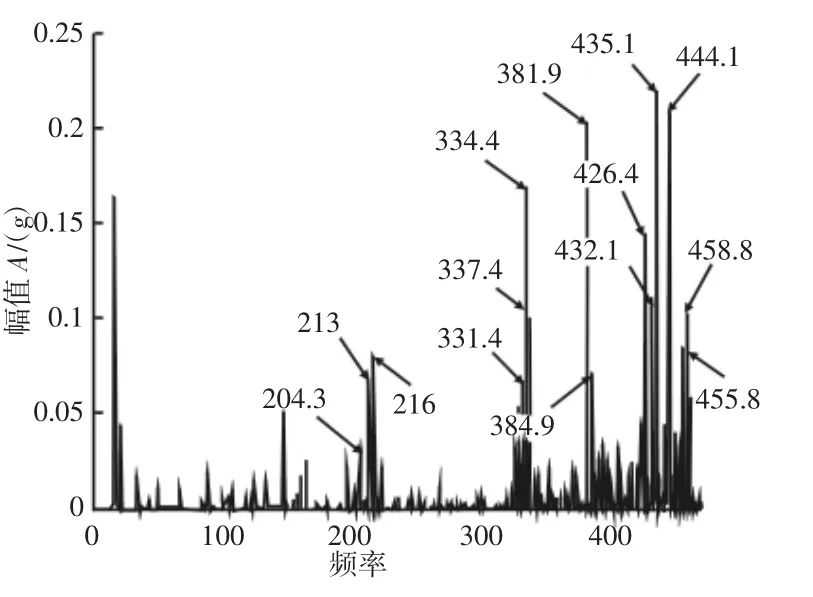
图8 太阳轮断齿时的试验振动响应信号频谱图Fig.8 Spectrum of Test Vibration Response for Sun Gear Broken

由图8可知，在太阳轮断齿故障下，响应信号同时受到太阳轮故障频率fs和行星架转频fc的调制作用，啮合频率及其倍频附近出现调制频率为fc和fs的边频带，如在频率fm-fs（约204.3Hz），fm-fc（约213Hz），2fm-4fs-fc（约381.9Hz），2fm-2fc（约426.4Hz），2fm+fc（约435.1Hz），2fm+fs（约444.1 Hz），2fm+2fs+fc（约458.8Hz）等处幅值比较明显。对比图6和图8可得，动力学模型所得频谱的边频带较小，这是因为行星齿轮系统模型复杂、参数众多，虽然对模型及参数进行了优化，但仍会与实际有一定差距，但动力学模型的频谱响应特性与试验所得结果基本一致，能够反映太阳轮断齿的实际故障状态。

5 结论

（1）建立了考虑振动传递路径时变效应的行星齿轮系统动力学模型，模型考虑了齿轮副啮合综合误差、齿侧间隙等因素的影响；（2）推导了太阳轮断齿故障下齿轮副的时变啮合刚度傅里叶级数表达式，并对所建模型进行求解，得到了太阳轮断齿时系统的频谱响应特性，即太阳轮断齿故障时，频谱幅值出现在kf¯m±（k，m，n为整数）位置处；（3）通过行星齿轮箱故障诊断试验台进行试验，将模型结果与试验结果进行对比，验证了所建立动力学模型的准确性，为行星轮系统的健康监测及故障诊断提供了一定的理论依据。