汽车发动机弹性支承隔振解耦方法

2020-03-27李阳

中国设备工程 2020年3期

李阳

（湖北交通职业技术学院，湖北武汉 430079）

1 发动机振动分析及对策

车辆的动力非常受电动机驱动，驾驶车辆时的路况会导致车身由于发动机不平衡和气压降低而振动。这是由于车辆的运行中宽带振动的频率是固定的，因此，振动强度会沿着振动频率的低频段集中。振动的形式主要可以分为垂直振动和水平振动。研究表明，非线性振动隔离技术在汽车发动机中的应用可以集中，并有效地控制宽频率条件下电动机的振动。而在高频条件下，仅需要确保所选择的材料足够，并且参数足以确保在不改变车辆和发动机的结构的情况下实现减小发动机的振动效果，可以促进功能结构的安全性和可靠性。但是，由于响应频率与非线性系统的励磁频率不匹配，因此，非线性振动难以充分理解发动机的运转状态。对于非线性系统，其振动隔离与动态系统的性能有关，因此，非线性系统存在一些限制。橡胶悬架技术是目前普遍使用的技术，可以有效地减少由低频电动机引起的振动。但是，通过将振动与高频带进行比较，机械设备的出色性能也起着重要作用，橡胶悬浮液分离技术导致高频范围内出现动态硬化，致使效果不佳。因此，必须在技术上进行更改。

2 汽车发动机弹性支承隔振的解耦方法

（1）振与解藕。在振动分离方面，并不需要解决振动系统的问题。要实现出色的隔振效果，可以控制振与解藕，而振动系统中存在以下振动:

系统在频域内的响应为：

式中：[H]为导纳矩阵，式（2）的展开式（3）写成：

导纳和系统各模态参数间有如下关系式：

当然，由于坐标的系数和真空的使用，导致的结果是:H变小，该系统将对冷的分离产生积极的影响。为了研究振动的谐波关系，需要综合系统子结构的动态特性，有必要确定故障程度和其他困难程度的定量特性。但是，对于解决方案，可以找到有关基础结构动态性质的正确规范。对于电动机的振动，一般要求如下：电机的振动模式围绕曲柄旋转。在电动机缓慢时，曲柄的固有频率将小于励磁频率的一半。发动机的垂直振动状态（主要是汽车的上下、来回运动），必须通过控制诸如垂直振动和前轮胎的旋转弯曲之类的频率来解决。在两种振动状态下，必须完全求解坐标。

（2）能量法解藕。发动机子系统中的振动有很多问题。过去，这是通过重组直接有效地实现的，基本方法是通过系统的中心主惯性轴调整轴向系统中的弹性元件解除藕动。因此，弹性中心主要是惯性轴或质量（cs）系统。当放置在中心时，没有弹性联轴器。在图1 中，指向弹性中心，点I 的位置由以下等式确定

弹性构件的几何被充分调节并且处于所需位置，只要它是橡胶组分的k 值（k 是橡胶组分的压缩刚度与压缩强度和剪切刚度之比）即可。

图1 弹性支承布置解藕结构方案

如果基本电动机轴与两个轴成一定角度分开，则电动机主体可以在驱动转矩（非弹性）的影响下围绕固定的“尖锐注意”（C3，C4）独立振动，可以在“弯曲轴”周围调整弹性，以解决该问题。在结构设计中实施上述步骤时，可以在大多数加盖固定系统中轻松操作。气缸机械具有固有的对称平面，因此曲轴与惯性轴“弯曲轴”之间的角度不是很大。使用“主轴”之一进行修改计算，比较简单容易，如果电动机结构没有清晰的对称平面，则面板的主轴（例如，现在很流行的全轮驱动车辆），由于发动机的原因，很难调整上述步骤，使得结构设计不同，如公式（4）。

上面的模型只能在方向上自由求解，优化解决方案的过程需要评估换挡，这是解决该问题的新方法。马达的支撑元件是具有润湿结构的橡胶的一部分，该润湿结构对应于系统的x 轴曲轴的方向，这说明Cl 具有作用在第一归一化坐标上的抽力。公式（l）可以写成

在新的主坐标系{q}下的微分方程式（5）变为：

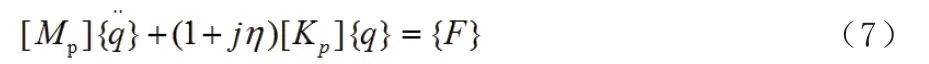
式中：[Mp]及[Kp]为对角阵。

在新坐标系{q}下的广义力{F}为：

由（8）式可知，新坐标系{q}下的广义力{F}由原来的1 个变成了6 个，即：

公式（7）可以解决问题，但振动分离问题还必须解决6 个自由度，这会增加归一化的力，并减小解，原始坐标的格式是解决问题的唯一方法，因为最好是自由解决隔振问题。

原始的标准化坐标x 方向相同，并且与差值成正比。因此，可以从广义上理解，并且系统从原始坐标含义中得出振动分析。通过计算机优化来检索制度矩阵的第i 行和第i列的非对角元素。如果要优化数学编程，则必须编写自己的非对角r 模式，但是值是不同的，因为每个元素w 看到的物理平均值不相等。为了提高计算的稳定性，应通过扩展上述优化模型，将相互速度扩展到振幅的定义。

（3）利用对称布置的V 形悬置组使振动系统刚度矩阵中的非对角元素(弹性耦合)为零作为解耦目标。这是一种弹性检测方法，其物理含义很清楚。系统的质量和刚度矩阵是对角线，在完全分解状态下，可以假设系统的振动应力为零振动数。在不完全状态下，弹性耦合系统的类型和程度可以由圆顶刚度矩阵确定为零，而不能由耦合系统的振动水平决定。在一般情况下，其永远不会为零，并且如果系统的刚度矩阵不是严格对角的，则两个自由度之间的弹性交换不支持振动一致性。在振动系统的基本惯性轴坐标系时，归一化质量矩阵是对角矩阵。尽管存在惯性键，但不同弹性系数之间的相互作用仍然很复杂。同时，许多自由方向都吸引了发动机燃烧的动力，如不平衡的旋转惯性，具有多个自由度来响应刺激。这阻碍了自然频率在驱动悬挂系统和其他车辆的声音系统之间的投射。因此，这不是评估振动水平的正确方法。

（4）以刚体模态振型向量中各个分量的相对大小来判断各自由度之间的振动耦合程度。这是识别模态振动耦合的最基本方法，机械含义很明确。如果每个状态向量中只有一个分量为0，而所有其他分量为0，那么我们可以假定系统的振动电压为零。实际上，在这一点上，可以将调制解调器矩阵视为一个单位矩阵，该矩阵乘积和单位矩阵仍然是矩阵。可以从属性中估价，模态质量矩阵和模态刚度矩阵必须是对角矩阵，质量矩阵和刚度矩阵也必须是对角线。因此，结论是振动没有相似性。即，如果系统矩阵的质量或刚度不是严格地对角矩阵，则模式矩阵可能不是同一矩阵。在振动机构的平移和旋转自由度这一点上，可能难以确定非零乘积的存在，以及在不同尺寸处发生振动的情况下的振动耦合程度和向量元素。例如，由于短期自由度和革命幅度，车辆的剧烈振动通常具有不同的质量和扭矩。因此，在该值（大约1 位数）中，状态下组件的相对大小通常由归一化电流自由度的相对振动反映出来。