基于径向疲劳仿真的铝合金轮毂寿命分析*

单 萍 郑忠才 高 岩 刘 娜 李 达

（1-山东建筑大学机电工程学院 山东 济南 250101 2-山东电子职业技术学院）

引言

随着环境的日益恶劣，众多行业都将“节能减排”作为企业的研发重点。而汽车行业选择将目光投向了新能源汽车产业，虽然新能源汽车可以降低排放对环境的影响，但仍旧面临许多问题。其中之一就是：如果整车车身质量过大则会造成电池消耗过大，续航里程缩短，充电次数增多，增加了电池的损耗，同时使用成本提高，这些都将不利于新能源车型的推广。所以汽车零部件和总成的轻量化设计已经成为新汽车开发制造的一个关键方面[1]。

研究表明，用铝合金代替低碳钢、铸铁或者高强钢可以实现30%～60%的减重效果，每千克铝合金的使用可以减少13～20 kg 温室气体的排放[2]。于是很多汽车企业选择利用铝合金轮毂代替原有的钢制轮毂。但是在铝合金轮毂被真正应用于汽车之前，需要对其进行车轮径向疲劳试验与弯曲疲劳试验。研究学者对弯曲疲劳试验的研究较为深入，而对车轮的径向疲劳试验研究较为匮乏，或者只考虑径向载荷对其的影响，而没有考虑胎压对其的影响，造成研究的不准确性。本文选择综合考虑两者的影响，对某铝合金轮毂进行仿真试验研究，并预测该轮毂径向疲劳寿命。

1 建立有限元模型及其边界条件

根据GB/T5334-2005《乘用车车轮性能要求和试验方法》的要求，当汽车在进行径向疲劳试验时，径向载荷的加载方向需要与转鼓表面垂直，同时径向加载方向与转鼓和车轮的中心连线需要在径向方向上保持一致[3]。具体的加载方式如图1 所示。

图1 车轮径向疲劳试验示意图

厂家给出的铝合金轮毂材料为A356（ZAI01A），它具有良好的流动性，气密性好，密度小，耐腐蚀，无热裂倾向，线收缩小以及易气焊等性能，并且具有较高的强度和塑性，因而能够满足轻载以及重载轮毂性能需求[4]，所以具有较好的应用性。厂家所提供的具体实物图如图2 所示，其具体材料性能如表1所示。

图2 铝合金轮毂实物图

表1 材料性能参数

对该型号铝合金轮毂采用四面体网格进行划分，单元尺寸设定为10 mm，经划分共得到714 605个节点，车轮划分之后的有限元模型如图3 所示。

图3 车轮有限元模型

在进行车轮径向疲劳试验时，需要将被检测的轮毂固定安装在法兰盘上，所以要对轮毂安装端面与法兰盘上的螺栓孔进行6 个自由度的全约束。具体的约束情况如图4、图5 所示。

图4 轮毂安装端面全约束

图5 法兰盘上的螺栓孔全约束

2 车轮载荷的施加

2.1 径向载荷的施加

在进行轮毂建模时选择采用Stearns.J 对于车轮与轮胎接触的研究成果[5]，即在有限元分析中对轮胎与车轮的接触部分的应力采用以余弦函数的方式进行施加，从轮毂中线至两侧某个角度依次减小，根据Stearns.J 的研究成果，θo大约为40°，具体施加方式如图6 所示。

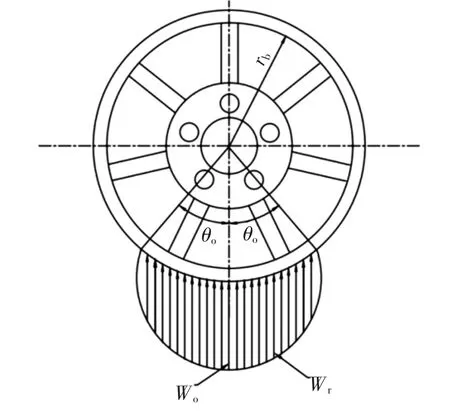
图6 车轮径向载荷分布力模拟施加图

车轮径向载荷的大小为：

式中：F 为车轮径向载荷，FV为车轮或汽车制造厂规定的车轮上的最大垂直静负荷或车轮的额定负荷，K为强化试验系数。

车轮径向分布力为：

式中：Wr为径向分布力，Wo为最大径向分布力，θ 为加载偏转角，θo为最大加载偏转角。

车轮径向力合力Fr为

式中：b 为轮胎座受力宽度，rb为轮胎座半径。

表2 为车轮径向疲劳相关数据。

表2 车轮径向疲劳相关数据

根据RAJUP Ramamurty 的试验结果得知，当K=2.0 时，此时最接近现实工况[6]，根据厂家提供的资料，可知FV取7 154 N，根据式（1）可知，F=14 308 N。由于加载的径向载荷呈现余弦变化，选择将轮毂均等分为36 份，即每份轮毂对应的角度为10°，根据上文提到的θo大约为40°，所以以轮毂中心线为界，两侧各取40°进行仿真试验，在每一份轮毂上实现余弦力的加载，由于模拟的为车轮动态旋转时的工况，所以设置36 个载荷步，每相邻的2 个载荷步之间旋转10°，能够使最大径向分布力均匀地绕车轮一周，方便观测车轮每一点的变化情况。

2.2 轮胎气压载荷的施加

在轮毂被安装在汽车上正常工作时，其表面需要安装轮胎，并对轮胎进行充气，所以需要考虑作用在轮毂表面的来自于充气轮胎的压力。根据学者研究表明：轮胎气压对于轮毂的疲劳寿命也有很大影响[7]。在选择对该轮毂施加轮胎气压时，根据GB/T2978-2008 对轮毂使用气压的规定，对应的气压为450 kPa。由于轮胎气压的作用表面为轮辋表面，于是将轮胎气压以面压力的方式施加在轮辋之上[8]。施加了径向载荷与轮胎气压载荷的轮毂如图7 所示。

图7 施加径向载荷与轮胎气压载荷的轮毂

3 结果分析

Von Mises 被称为第四屈服准则，其条件使当材料的八面体上的剪应力达到某一极限值时，材料开始屈服。第四强度理论认为形状改变比能是引起材料流动破坏的主要原因。由于车轮主要是以疲劳破坏为主，所以选用第四屈服准则作为分析评价参数比较合适[9]。

在运行完36 个载荷步之后，观察最大等效应力结果，选取其中的3 个特殊载荷步进行比较分析，分别是最大径向力沿Y 轴如图8 所示、最大径向力直对螺栓孔如图9 所示与最大径向力在两螺栓孔之间如图10 所示的应力云图。

图8 最大径向力沿Y 轴

图9 最大径向力直对螺栓孔

图10 最大径向力在两螺栓孔之间

提取这3 个特殊位置的最大应力值节点分别是5 772 节点、5 771 节点与5 730 节点，如图11 所示。观察该节点在最大径向力处于不同位置时的应力变化，可以看出危险点是随着最大径向力位置的不同是处于不断变化的状态，但是节点的位置是非常接近的，即最先发生破坏的位置可以看作近似一致。

图11 不同工况下的最大等效应力值

4 名义应力法预测疲劳寿命

按照计算疲劳累计损伤参量的差异，疲劳寿命分析方法有名义应力法（适用于高周疲劳）、局部应力应变法（适用于低周疲劳）和应力应变场强法。由于轮毂的径向疲劳属于高周疲劳，同时根据哈尔滨工业大学崔胜民教授研究成果，用名义应力法预测车轮疲劳寿命的可靠度较高，并且比较接近实际工况[10]。所以在预测轮毂疲劳寿命时选取该方法。

4.1 名义应力法理论分析

根据研究表明，对于极限拉伸强度小于1 400 MPa的钢材，其疲劳极限为

式中：σb为极限拉伸强度。

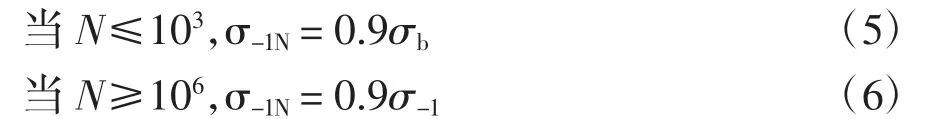
当N=（103～106）时，由N=103，σ-1N=0.9σb、N=106，σ-1N=0.9 σ-1的两点在双对数坐标上直线相连，这个直线就是N=（103～106）间的S-N 曲线，其表达式为：

式中：σ-1N为当寿命是N 时，对称弯曲疲劳极限的值。

由于原始材料的S-N 曲线只能代表标准光滑试件的疲劳性能，而实际零件的表面情况和尺寸与标准试件有着很大的区别。因此在做某一个零件的疲劳寿命时，需要对原始材料的S-N 曲线进行修正，计算出的疲劳寿命才更为可靠接近。查阅机械手册，知该型号铝合金车轮的有效集中系数为1.1，尺寸系数为0.72，表面加工系数为0.95，利用以上数据对原始材料的S-N 曲线进行调整，如图12 所示。

4.2 名义应力法结果分析

由于车轮在径向疲劳试验中受到的循环应力是不对称的，危险点在一个循环周期后其平均应力不为0。因此常按照下式将平均应力折算为等效的对称循环应力幅[11]。

图12 修正后的材料S-N 曲线

式中：φ 为不对称循环系数，σa为应力幅值，σm为平均应力。

根据上文第四屈服准则所得出来的危险节点，选择进一步观察这3 个节点的疲劳寿命特征，如表3所示。

将危险点的等效应力幅提取出来，在S-N 曲线上进行差值运算，即可求得铝合金轮毂危险节点的疲劳寿命，选取最小的循环次数作为该型号轮毂的疲劳寿命，从而进行计算。经计算得出该轮毂的径向疲劳寿命为614.26×104次，符合国家最低径向疲劳寿命标准，并且可以继续进行优化。

表3 轮毂各应力最高点的等效应力幅及疲劳寿命

5 结论

1）利用印记功能，将铝合金轮毂进行36 等分，有效地解决了输入反函数载荷困难的问题，并且36等分只作为一个思路，后续设计人员可以根据自身设计情况对模型进行不同等分，并且在考虑类似反函数载荷时，选择该方法的使用，减少运算时间与所需内存。

2）利用该软件进行变加载的施加，实现了径向载荷由静态施加至动态变化施加的问题，更加接近于实际工况同时提高仿真的准确度。

3）利用修正后的S-N 曲线，分析出该型号轮毂的径向疲劳寿命，并且获得该型号危险集中点，使后续设计人员在进行设计时，着重对该危险集中区进行加固，提高了安全性，为后续的设计与优化打下了基础。