一种基于虚拟阵元的超波束形成方法*

马晓强，江 宁

（1.四川邮电职业技术学院通信工程系，成都 610067；2.电子科技大学信息与通信工程学院，成都 611731）

0 引言

在雷达、声纳、通讯等领域中，常规波束形成（Conventional Beam-Forming，CBF）能够对波达方向（Direction of Arrival，DOA）进行信号合成、增强输出数据中信噪比含有量，易于实现，宽容性好，在阵列信号处理中被广泛应用［1-5］。但该方法存在主波束宽、旁瓣级高、能量泄漏等缺点，易引起旁瓣干扰，不利于弱目标检测。

为了克服CBF 方法存在的主波束宽、旁瓣级高等缺点，研究学者提出了一种波束锐化方法：超波束形成方法（Hyper Beam-forming，HBF）［6-8］，该方法在阵列孔径保持不变情况下，有效减小了CBF 主波束宽度，抑制了旁瓣，解决了空间加权方法在进行旁瓣抑制和波束锐化折中选择问题。

由现有文献［9-12］可知，现有HBF 方法的实现过程通常为通过对接收阵分子阵做波束形成，形成同一方向波束对，然后在对该波束对进行和差波束运算，最后对和差波束运算结果进行合成，使波束图锐化。该过程在信噪比较高情况下，可很好实现主波束锐化和旁瓣抑制［13-15］，但该过程分子阵所用阵元数为接收阵一半，在实现主波束锐化和旁瓣抑制时，其所能达到的最低信噪比有限，在一定信噪比下不能实现对弱目标检测。

为了提高HBF 在低信噪比应用中的鲁棒性，依据阵元间协方差矩阵同一斜对角线上不同元素具有相同相位差的特点［16-17］，按互相关方法对接收阵进行虚拟扩展；然后按HBF 思想分子阵分裂波束形成；最后对分裂波束形成结果进行合成，得到改善的超波束形成结果，本文称之为基于虚拟阵元的超波束形成方法（Hyper Beam-forming Based on Virtual Array Element，VAEHBF）。

数值仿真和实测数据处理结果表明，相比HBF，本文方法通过对接收阵进行虚拟扩展，在保持分辨力不变的情况下，进一步提高了合成波束增益，对最低信噪比的适应能力得到了3 dB 改善，提高了HBF 的目标检测性能及方位估计能力。

1 HBF 方法

1.1 基本原理

图1 HBF 分裂波束示意图

为了更直观说明HBF 输出波束过程，如图1 所示，对于相邻阵元间距为d 的N 接收阵，波长为、方位为θ 的目标信号，则相邻阵元接收目标信号相位差为。期望波束方位为θ0，相邻阵元插入相移因子。令目标信号为单位信号，以阵元1 作为参考点，左、右子阵对应波束表达式RL和RR可分别表示为［13］

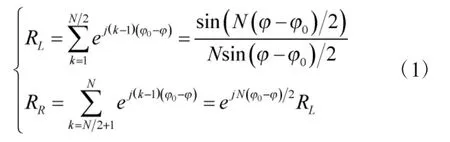
根据HBF 合成中和波束RS、差波束RD［4-5］表达式，可得RS和RD的输出为

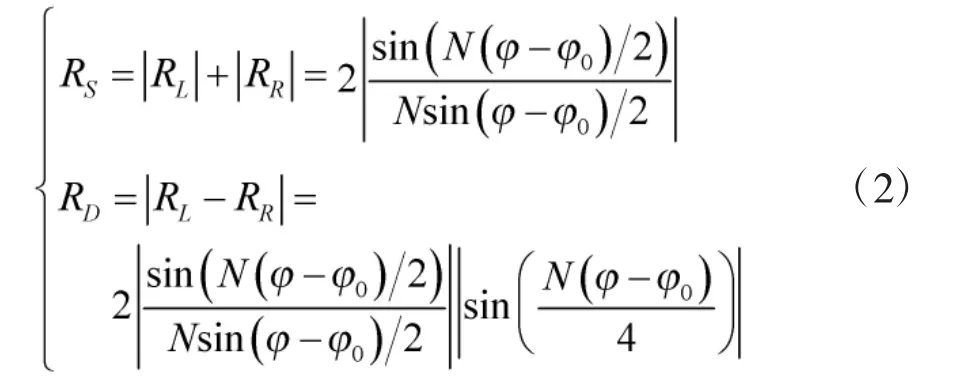
根据HBF 合成波束公式，RH输出为

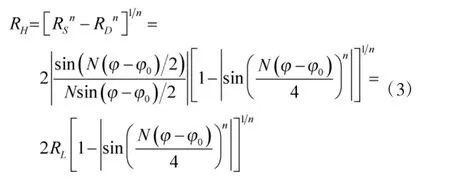
式中，n 为HBF 阶数，通过调整n 可获得相应宽度主波束输出。n 通常取n∈［0.3，1］，随着n 减小，HBF 输出主波束宽度减小。

1.2 性能仿真

为了对HBF 基本原理和实际应用效果做进一步说明分析，接下来采用阵元数为N=16 的半波长接收阵进行数值仿真说明，仿真结果如下。

由图2 可知，在波达方向上，“差波束”最小，“和波束”最大，且两者旁瓣位于相同方位上，因此，可通过两者相减获得窄波束和低旁瓣级波束输出。

图2 和波束与差波束的输出

图3 进一步验证了图2 仿真结果和HBF 特性，即当目标方位和波束合成方向相同时，RS=2RL，RD=0；当目标方位和波束合成方向偏离较大时，RS减小，RD增大，进而使式（3）输出RH得到锐化。

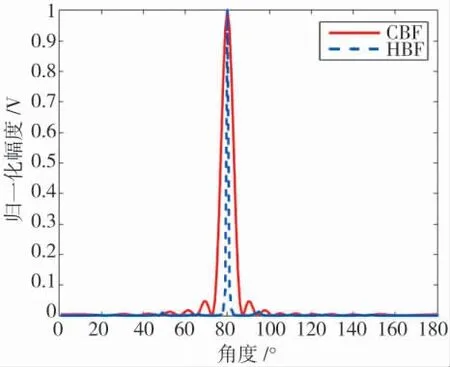
图3 CBF 与HBF 输出波束比较

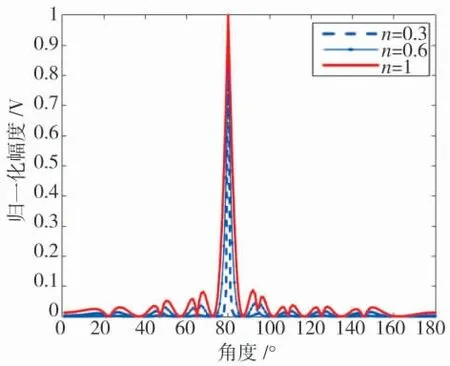
图4 不同阶数下的HBF 输出波束

另外，由图4 可知，随着阶数n 减小，HBF 主波束宽度和旁瓣级同时减小。

该仿真结果表明，HBF 可在阵列孔径保持不变的情况下，有效减小了CBF 主波束宽度，抑制了旁瓣，解决了空间加权方法在进行旁瓣抑制和波束锐化折中选择问题。

2 VAEHBF 方法

2.1 基本原理

由式（3）可知，RH输出波束对目标探测能力受RL影响。为了提高RH输出波束对目标探测能力，VAEHBF 依据阵元间协方差矩阵同一斜对角线上不同元素具有相同相位差的特点，对协方差矩阵同一斜对角线上不同元素进行叠加运算，可虚拟出与接收阵相同数据的接收阵元。

令接收阵接收数据协方差矩阵为R，对R 进行互相关处理可得一维新数据X'。

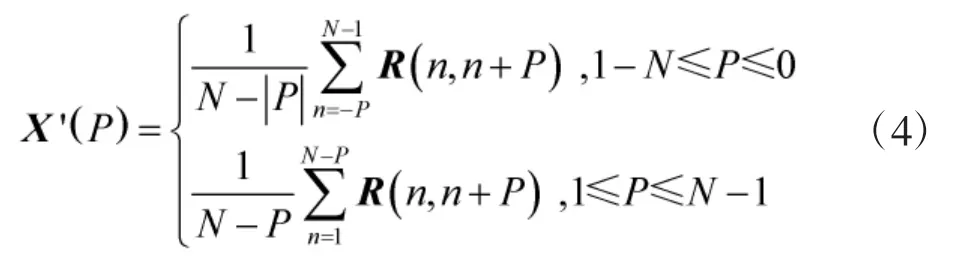
此时，可按图5 所示分子阵方法对扩展后接收阵进行分裂波束形成。

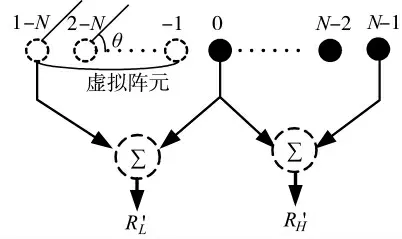
图5 VAEHBF 分裂波束示意图

同样，令目标信号为单位信号，以虚拟阵元1-N作为参考点，左、右子阵对应波束表达式RL'和RR'可分别表示为

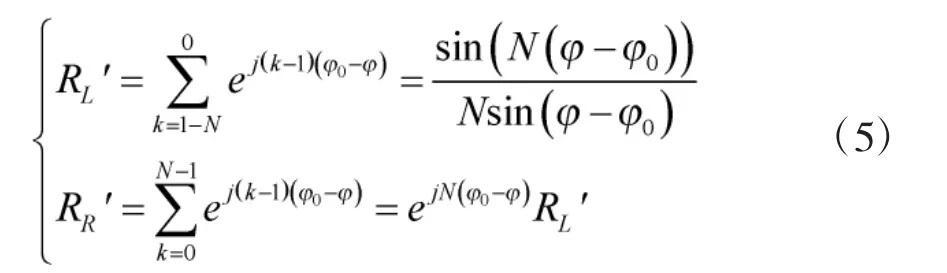
由式（5）可得RS'和RD'的输出为

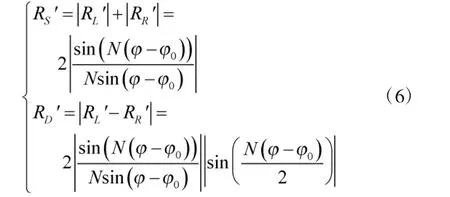
由式（6）可得RH'输出为

由式（7）可知，RH'输出波束对目标探测能力受RL'影响。

根据空间增益理论可知，采用RL'和RL形式所得空间增益分别为

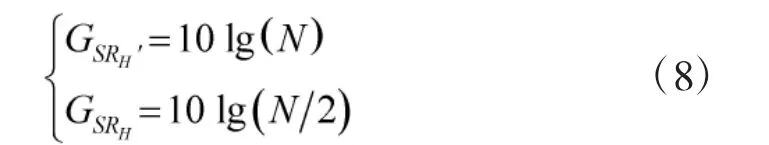
式中，log（·）以10 为底对数函数。

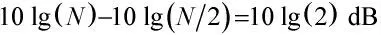
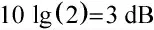
2.2 实现流程及运算量分析

由第2.1 节理论分析可知，VAEHBF 方法可分为如下步骤实现：

步骤1）对接收阵接收数据进行共轭相乘，得到接收阵接收数据协方差矩阵R；

步骤2）按式（4）对协方差矩阵R 进行互相关处理，可得一维新数据X'；

步骤3）按图5 分子阵方法对扩展后接收阵进行分裂波束形成，可得左、右子阵对应波束表达式RL'和RR'。

步骤4）由式（5）和式（6），根据相应阶数n，得到相应超波束形成结果。

由以上实现过程可知，VAEHBF 方法相比HBF方法，运算量增加量主要为：增加了步骤1）和步骤2）运算以及步骤3）中分子阵阵元增加1 倍波束形成运算。总的计算复杂度增加了N2+N 复乘运算和N（N+2）复加运算；随着计算机技术的进步，以上N2+N 复乘运算和N（N+2）复加运算的增加对VAEHBF 方法在实际应用中的影响有限。

2.3 数值仿真分析

为了对比VAEHBF 与HBF 方法对最低信噪比的适应能力，同样采用阵元数为N=16 的半波长接收阵进行数值仿真说明。图6 为不同输入信噪比下，按式（9）计算200 次独立统计所得方位估计值的均方根误差（Root Mean Square Error，RMSE），图7为正确检测目标概率；图8 和图9 为输入信噪比-10 dB 情况下，由2 种方法所得方位历程图。图10为某一时刻由2 种方法所得波束图。

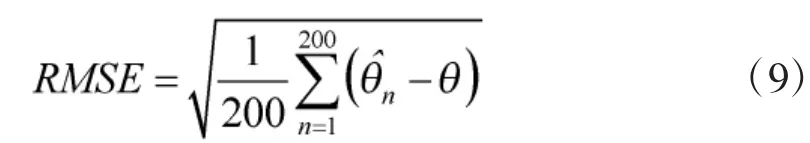
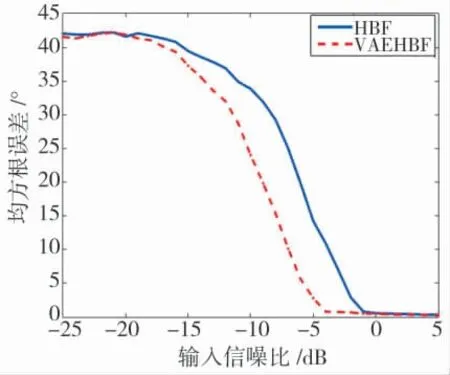
图6 方位估计均方根误差

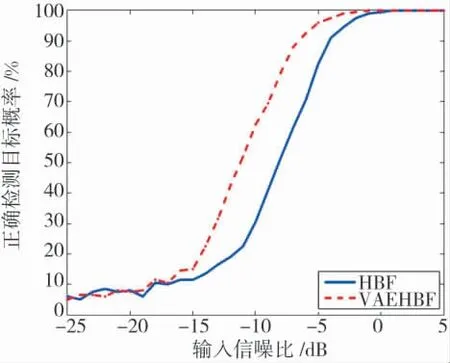
图7 正确检测目标概率

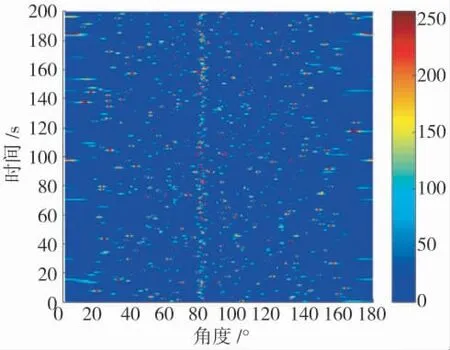
图8 HBF 所得方位历程图

图9 VAEHBF 所得方位历程图

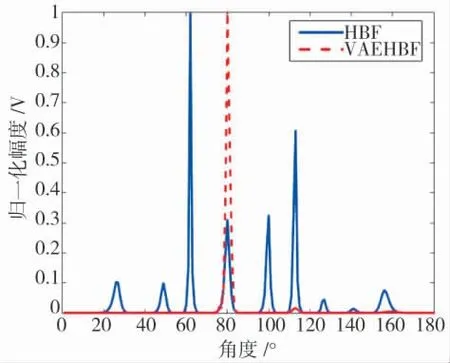
图10 波束图

由图6 和图7 可知，由于VAEHBF 通过对接收阵进行虚拟扩展，提高了分子阵波束形成空间增益和探测能力，在同一均方根误差情况下，相比HBF方法，VAEHBF 方法对目标的检测能力提高了3 dB，数值仿真结果与理论分析一致。

同时，由图8 至图10 可知，相比HBF 方法，VAEHBF 方法通过对接收阵进行虚拟扩展，提高超波束形成对最低信噪比的适应度，在信噪比为-10 dB情况下，VAEHBF 方法可有效实现对80°目标的检测，而在HBF 方法所得波束中，60°、100°和120°处背景噪声形成峰值已超过80°处目标信号形成的峰值，无法实现对80°处目标有效检测。该结果与图7所示结果相对应，即在信噪比为-10 dB 情况下，HBF 方法对目标的正确检测概率只有35 %左右，而VAEHBF 方法对目标的正确检测概率为70%左右，远大于HBF 方法对目标的正确检测概率。

3 实测数据处理

为了进一步说明VAEHBF 与HBF 方法在实际应用中效果，采用实测数据对其进行分析说明，本次实测数据为进行目标检测试验所得，实验采用32元水平线阵接收信号，阵间隔为1 m。

本次处理实测数据长度为120 s，所用采样率为fs=5 kHz。滤波器频带为fl=600 Hz～900 Hz，图11 和图12 为HBF 和VAEHBF 所得方位历程图。

图11 HBF 所得方位历程图

图12 VAEHBF 所得方位历程图

由图11 和图12 可知，相比HBF 方法，VAEHBF 方法通过对接收阵进行虚拟扩展，可以在不同时刻清晰地显示80°～110°内不同方位处的弱目标运动轨迹。实测数据处理结果进一步得到证实，相比HBF 方法，VAEHBF 方法在保持分辨力不变的情况下，可进一步提高合成波束增益，提高了目标检测性能及方位估计能力。

4 结论

本文提出了一种基于虚拟阵元的超波束形成方法，该方法依据阵元间协方差矩阵同一斜对角线上不同元素具有相同相位差的特点，首先按互相关方法对接收阵进行虚拟扩展；然后按HBF 思想分子阵分裂波束形成；最后对分裂波束形成结果进行合成，提高了HBF 对最低信噪比适应能力。理论分析、数值仿真和实测数据处理结果表明，相比HBF，本文方法通过对接收阵进行虚拟扩展，在保持分辨力不变的情况下，进一步提高了合成波束增益，对最低信噪比的适应能力得到了3 dB 改善，提高了HBF的目标检测性能及方位估计能力。