水下机器人试航速度的类物理数值方法预报

吴利红， 张爱锋， 李一平， 封锡盛， 王诗文

(1. 大连海事大学 船舶与海洋工程学院，辽宁 大连 116026；2. 中国科学院沈阳自动化研究所 机器人学国家重点实验室，辽宁 沈阳 110016)

预报水下机器人(autonomous underwater vehicle，AUV)定常航行的巡航速度和非定常运动的操纵性能不仅是评估其推进系统性能的重要指标，还有助于提高AUV航程估计，能量估算和减少定位误差和AUV丢失的风险。采用类物理的数值方法进行海洋载体操纵预报是数值模拟的目标。此方法应用真实模型模拟螺旋桨高速旋转，能反映船桨舵内在作用机理，再现流场特征。但它具有模型复杂，网格尺度相差大，载体各部件相对运动复杂，高频与低频运动混合的模拟难点[1]。自20世纪90年代美国海军提出这个概念以来，直至2010年左右陆续有研究成果。如Chase等[1]、Pankajakshan等[2]、Poremba等[3]对潜艇自航运动进行了数值模拟；Mofidi等[4]对集装箱船KCS带全附体桨舵的ZigZag操纵运动的模拟；Carrica等[5]对水面战舰的随浪横甩运动进行自航模拟；沈志荣[6]对水面船舶操纵运动进行数值模拟。以上研究均采用动态重叠网格法，在边界移动时无需网格更新，但须实时确定移动边界与背景网格的重叠区域，这是数值误差的源头[7]。而移动网格法在边界移动时网格也随着运动，运动更符合拉格朗日描述法，但边界移动常导致复杂的网格运动，从而引起网格畸变和网格质量降低，影响数值计算精度。受此限制，移动网格法主要应用在二维物体的运动：圆球的振动，鱼类的摆鳍运动[8]和三维物体的有限区间或简单的运动，如翼的偏转[9]，预定义AUV直航对接运动[10]。而本文则采用多块动态混合网格方法[11]解决移动网格的网格畸变和数值精度差的问题[12]，实现AUV自航试验的数值模拟，获得了AUV巡航速度预报，再现了AUV自航过程非定常运动的航行特性。

1 水下机器人自航模型建立

AUV为改进型REMUS AUV，L=1.7 m，D=0.191m[13]。具有椭球型艏、圆柱形平行中体和圆锥型艉。艉部有“十字”型舵翼以及一个MAU4-40，直径d=0.156 m的螺旋桨。AUV艏、舯和艉3段以及舵翼采用结构网格绘制，螺旋桨采用非结构网格离散。图1为AUV带舵翼和螺旋桨的网格图。大地坐标系为oxyz,ox为AUV对称轴，向艏为正(向前)；oy垂直向上为正；oz指向右舷。

图1 带桨和舵的AUV网格模型Fig.1 Grid model of AUV appended propeller and rudders

图2为AUV带桨舵流域在对称面上网格分区，分区划分是根据AUV的运动趋势确定的。流域包含 6个分区。分区Ⅰ包含AUV和舵翼表面的四边形网格以及近场边界层区域的六面体结构网格；分区Ⅱ包括螺旋桨表面的三角形网格以及螺旋桨扰动子区域的四面体非结构网格；分区Ⅲ包含AUV、螺旋桨和舵翼扰动区域的六面体结构网格；分区Ⅳ为AUV从艏部延伸到远场的航行区域网格，靠近艏部加密，远场较为稀疏，由六面体结构网格构成；分区Ⅴ为从AUV艉部延伸到远场的结构网格区域，靠近AUV艉部为加密区，远场为稀疏区，也由六面体结构网格构成；外围非结构网格区域为分区Ⅵ。

图2 动网格分区Fig.2 Dynamic meshing zones

在AUV自航推进数值模拟过程中，网格运动区域限制在图2的AUV直航窄条带区域，这有利于局部扰动区域梯度的捕捉。其中分区Ⅱ既有随螺旋桨的旋转运动，又有随AUV的直航运动；分区Ⅰ和Ⅲ仅随AUV作直航运动；分区Ⅳ和Ⅴ分别为网格压缩区域和拉伸区域，在分区Ⅳ的最前端为静止壁面，采用动态层方法对区域Ⅳ的最前端网格进行压缩合并，因此最前端为网格消亡区域；分区Ⅴ的最后端为动态层网格的拉伸区域，为网格增长区域。外围区域Ⅵ为网格变形区。各个分区之间的连接采用非一致连接。这种多块结构网格和非结构网格混合的网格构成方法，以及采用动态层网格更新方法，是借鉴了动态重叠网格的子区域网格运动的思想，从网格构建质量、网格更新质量和网格更新速度等方面着手，提高数值求解的速度和计算精度。

AUV自航推进过程数值模拟中，AUV和螺旋桨之间力和速度的传递可以采用用户自定义函数UDF(user defined function)进行编写，嵌入到程序中[14]：首先，AUV静止，螺旋桨以恒定转速旋转，产生推力，将此推力保存同时将推力传递给AUV；AUV读取螺旋桨推力，同时实时求解URANS(unsteady reynolds averaged navier-stokes)方程，获得AUV的阻力。AUV在推力和阻力的联合作用下，通过在6-DOF方程加载推力和实时阻力，求解载体的加速度，并采用龙格库塔积分获得AUV实时速度V；此速度传递给螺旋桨，使AUV拖曳螺旋桨以V航速运动；随着AUV航行，AUV的尾流场更新，影响螺旋桨的进流场，螺旋桨在新的进速和转速下产生新的推力，重新记录此推力并传递给AUV；AUV在阻力作用下，获得新的航速，如此重复，直到AUV的推力T与其航行阻力R接近平衡，速度曲线趋于稳定，加速度接近为零。或对比航速与多参考系坐标[15](multiple frames of reference, MFR)的定常自航点航速，两者误差在5%内，也认为达到自航点。记录此时的推力、阻力、速度历史数据，保存和分析。

2 水下机器人自航数值结果与分析

2.1 受力和速度

AUV 以不同转速从静止自航推进，最终会趋于匀速状态。分别假定AUV以300、450、600 r/min 3种转速航行，每种转速自航一次，迭代步长为螺旋桨旋转1°对应的时间，每个外循环包含内循环20次，收敛精度为10-4。如图3分别为转速为300、450和600 r/min的自航螺旋桨推力和AUV阻力的历史变化曲线。推力和阻力曲线在数值求解中有点振荡，这是动网格数值求解引起的不稳定现象。阻力部分振荡主要是由于载体低速巡航采用了和螺旋桨高速旋转的小时间步引起的。随着速度增加，推力减小，阻力增大，最终推力和阻力平衡，速度会趋于一个恒定的速度，这个速度即为该转速下的自航点。3种转速可得3次航速历史变化，如图4所示，可得3个不同的自航点。转速越大，达到匀速的时间越短。600 r/min，需要约9 s, 可达到匀速1.55 m/s；450 r/min，需要约10.53 s, 可达到匀速1.15 m/s； 300 r/min，需要约14.39 s, 可达到匀速0.74 m/s。同时，转速越大，起始加速度越大。

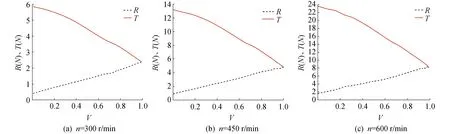
图3 不同转速下AUV自航阻力和推力变化Fig.3 The resistance (R) and Thrust (T) of AUV self-propulsion at different rotation speeds

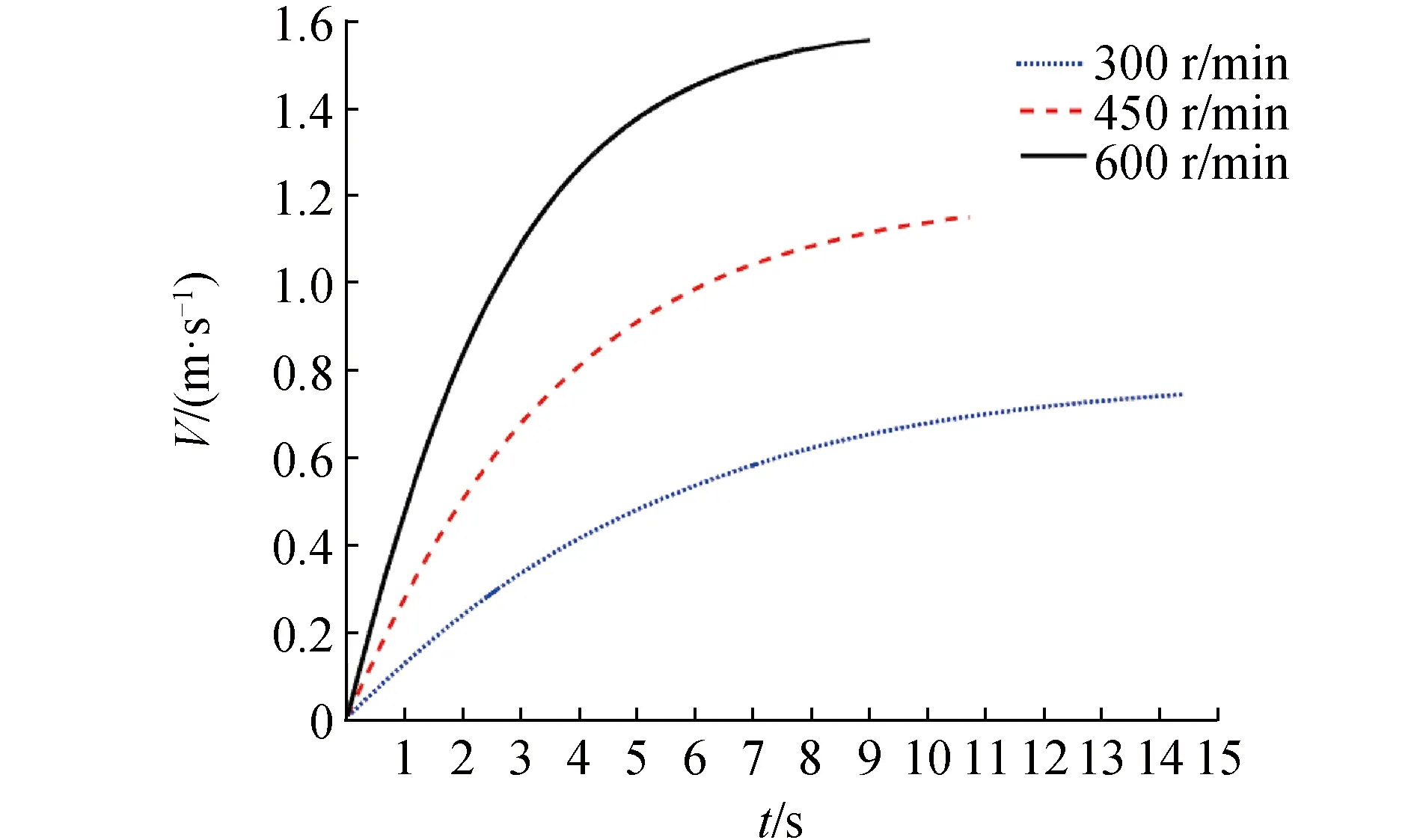
图4 不同转速下AUV自航过程的航速变化Fig.4 Velocity history (V) in AUV self-propulsion at different rotation speeds (n)

2.2 数值验证

为了验证数值模拟结果的准确性，将AUV自航的数值结果与水池试验(试验在中国科学院沈阳自动化所的深水水池：L×B×D=25 m×15 m×9 m)结果进行对比。图5记录了螺旋桨转速为300 r/min的AUV速度历史数据。包括5次试验结果，以离散数据点表示：Exp1、Exp2、Exp3、Exp4 和Exp5；数值结果以实线表示。数值模拟不受试验水池边界的限制，因此数值模拟的时间较长。数值结果和试验结果吻合良好。此外，为了验证不同转速下AUV自航点的可靠性，将本文的结果与多参考坐标系MFR(multi-frame of reference)的结果进行对比验证，如图6所示，获得的自航点速度略低于MFR，误差在5%以内。在一段转速范围内，航速和转速成正比。这是因为相近的一段转速范围内，推力系数接近常数，阻力系数接近常数。螺旋桨推力与转速成平方，匀速后推力与阻力相等，阻力与速度成平方，则自航点速度和转速成正比。这个结论有助于更快找到不同转速下的自航点。由转速和航速的关系，根据设计航速1.5 m/s的要求，对图6进行插值，可得对应自航点的转速为570 r/min。

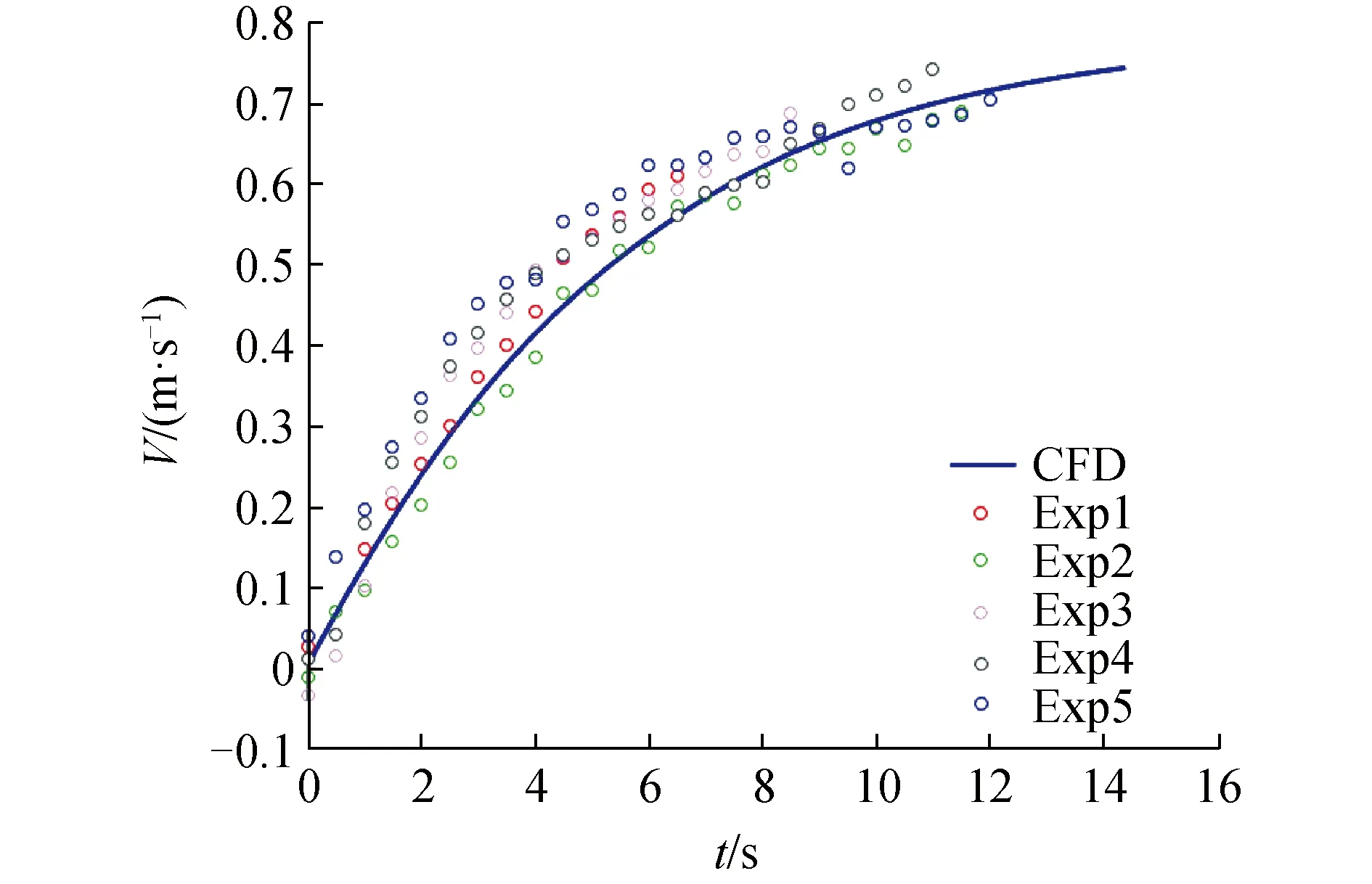
图5 AUV自航速度变化的试验和数值结果 (n=300 r/min)Fig.5 The velocity history from experimental and numerical results in AUV self-propulsion at n=300 r/min

图6 自航点对应的转速Fig.6 Approaching velocities vs. rotating speeds

2.3 流场分析

图7为转速n为300、 450和600 r/min时达到匀速直航的AUV对称面上的速度云图(注：远场速度为零)。可见，转速越大，螺旋桨的艉迹越明显，梢涡强度越大，向后推水的水速度越大，反作用力越大，则推力越大。且转速越大，AUV艏部的速度扰动流场范围越大，表明AUV达到自航点对应的速度越大。3种匀速状态时，AUV艏部最大截面处都产生了艏涡，且随着速度增加，艏涡范围加大，表明AUV艏部粘压阻力增加。随着AUV速度增加，AUV艉部截面变化区域开始产生艉涡(n=600 r/min)，表明艉部速降增加，艉部粘压阻力增加。同时，3种航速时，AUV表面都有较明显的边界层，从艏至艉逐步增厚。

图7 AUV不同转速对应的自航点速度云图Fig.7 Velocity contours of AUV at different self-propulsion points with varying rotation speeds

图8为设计航速1.5 m/s对应转速570 r/min 的AUV自航过程4个典型时刻(t为0.1，3,4.9和6.9 s)对称面上AUV的速度分布(右图)和螺旋桨艉迹局部放大图(左图)。相应的压力云图如图9所示。可见，当转速一定时，AUV速度较低时，螺旋桨艉迹强，表明螺旋桨此时的推力较大(这与螺旋桨的敞水性能曲线一致，和图3的推力曲线一致)。螺旋桨叶梢曳出的梢涡出现重叠；随着AUV航速增加，梢涡强度降低，表明螺旋桨推力减少。但是梢涡分离清晰可见，这是由AUV航行时的艉迹反向作用引起的。

图8 AUV自航对称面上不同时刻的速度云图(n=570 r/min)Fig.8 Velocity contours of AUV self-propulsion on the symmetry plane at different times with n=570 r/min

图9 AUV自航对称面上不同时刻的压力云图(n=570 r/min)Fig.9 Pressure contours of AUV self-propulsion at the symmetry plane at different times with n=570 r/min

随着AUV航速的增加， 螺旋桨产生的推力在变小，这点在图9的左侧压力云图中清晰可见。低速时，螺旋桨叶面的高压值很大，叶背的低压值也较大，导致两者的压差较大，因此推力较大；随着AUV速度增加，叶面高压值减小，叶背低压值也减小，两者的压差变小，则推力也在减少。但是，随着螺旋桨持续旋转，只要AUV推力大于阻力，AUV就获得加速，随着AUV速度增加，AUV艏部速度绕流场范围加大，艏部驻点的压强增加，导致AUV艏艉压差阻力增加；同时艏肩部速度增加，导致摩擦阻力增加，AUV总阻力也在增加，直至与逐渐减小的推力平衡，达到匀速直航，即达到自航点。随着螺旋桨推进AUV自航，AUV艉迹延长。螺旋桨艉迹梢涡强度随AUV速度增加弱化。同时，在螺旋桨毂帽附近有一股根涡，和AUV航行方向一致，流速大小随着AUV速度增加而增加。

3 结论

1) 水下机器人不同转速对应的最终巡航速度不同。300、450和600 r/min分别对应的巡航速度为0.74、1.15和1.55 m/s。AUV的巡航速度1.5 m/s对应的转速是570 r/min。

2) AUV自航稳定所需时间与AUV转速大小有关。转速越大，加速度越大，稳定需要时间越短。300、450和600 r/min稳定分别需要14.39、10.53和 9 s。

3) 在螺旋桨转速变化较小的范围内，AUV的自航点速度和转速成正比关系。

4) AUV自航时，螺旋桨旋转运动曳出梢涡和根涡。梢涡强度随着AUV航速增加而降低，运动方向与AUV航行方向相反。根涡大小随AUV航速增加而增加，方向与AUV航行方向一致。

5) 螺旋桨推力的变化起源于其叶面和叶背压差变化。AUV以恒定转速自航，推力随速度增加而减小。