GNSS精密单点定位算法研究
2020-03-25杨晓伟焦步青焦泽珍
杨晓伟,焦步青,焦泽珍
(中煤平朔集团有限公司 地质测量中心,山西 朔州 036000)
精密单点定位[1](PPP,Precise Point Positioning)利用IGS或iGMAS中心提供的精密轨道、钟差和地球自转等精密产品,以及移动端载波和伪距观测数据即可得到高精度的定位结果[2]。同时,精密单点定位技术不需要全球密集参考网组合观测值,不受基准站的影响,只需要4颗及以上的可见卫星即可得到实时位置信息。所以该技术在交通导航、精密农业、地震监测等领域具有广阔的应用前景。但是,精密单点定位技术存在以下缺点:单GPS系统可见卫星数较少;需要已知精密轨道、钟差等精密产品;模糊度收敛速度慢;模糊度固定较困难;精密产品严重依赖于全球参考网,所以很难达到实时导航定位效果。随着美国GPS和俄罗斯GLONASS现代化的推进,北斗导航系统的成功全球组网,多系统可以大大增加可见卫星数,更多频率观测值可以组成更多较优的组合观测值,大大提高定位的精度和可靠性,为精密单点定位的快速模糊度固定提供了可能,因此,多系统精密单点定位导航定位成为了未来的必然趋势,尤其是在部分卫星遮挡的复杂环境下[3]。
1 精密单点定位函数模型
在GNSS测量中,伪距与载波相位的观测方程如下:

式中:P为伪距观测值;渍为载波观测值;c为真空中的光速;VtR为接收机钟差;Vts为卫星钟差;Vion为电离层延迟;Vrtop为对流层延迟;λ为波长;N为整周模糊度;δρ 为卫星星历误差对测距的影响;δρmul为多路径误差;εp为伪距观测噪声;εφ为载波观测噪声;ρ 为卫星和接收机的几何距离项,ρ=为接收机位置坐标,(xs,ys,zs)为卫星坐标。
利用IGS发布的精密钟差和精密星历产品,通过拉格朗日内插的方法可以获得式(1)、式(2)中的卫星精确三维坐标和卫星钟差[4]。固体潮、海潮、地球自转、极移、相对论效应等误差可以通过各自的误差模型来加以修正。电离层延迟可以通过消一阶电离层组合观测值进行消除[5]。
2 精密单点随机模型
随机模型是指将观测值之间存在的相关性及随机性通过算法表现出来的模型。由于观测值在观测的过程中不可避免地存在偶然性,故一般认为观测值是一个随机变量。一般采用方差矩阵来描述观测值的精度,用协方差矩阵来描述观测值之间的相关性。对于观测值向量L,存在其方差-协方差阵D。

一般来说,伪距观测值与载波观测值之间不存在相关性,故可以忽略伪距组合观测值和载波组合观测值之间的相关性。因此,在建立观测值的随机模型时,需要对观测值进行定权,毕竟每一项观测值的精度不同。研究表明,伪距及载波测量信号的信噪比与卫星的截止高度角息息相关。因此,可以通过卫星的截止高度角来为观测值M(E)定权:

式中:E为卫星高度角,(°)。
3 抗差Kalman滤波模型
传统上的粗差处理方法主要有以下2类:①将粗差当做异常观测值,采用数学模型进行探测,然后在原始观测数据中进行剔除;②通过选权迭代降低粗差所在观测值的权值,从而减弱粗差对结果的影响。本文的抗差Kalman滤波采用的是第2种方法[6]。
传统抗差Kalman滤波是采用新息向量来检测,即当预测值与观测值差值较大时认为存在粗差[7],但是现有研究结果表明,不同观测精度的观测值采用新息向量无法有效检测较高精度观测值的粗差异常情况[8]。而验后残差向量能够完美地反映不同观测精度观测值的异常情况,同样采用验后残差向量构造抗差因子,从而降低异常观测值所在的观测权矩阵,从而达到抗差的效果。为了减弱参数间的相关性,对Kalman滤波过程进行迭代处理,从而大大减弱粗差的影响。
Kalman滤波的新息向量如下式:


而验后残差向量Vk可表示为:




式中:上标为验前或预测信息;xk为第k历元的待估参数向量;Hk为观测方程的系数矩阵;zk为第k历元的观测值;dk为新息向量;Rk为各个观测量误差协方差阵为验前的协方差矩阵,Kk为增益矩阵;νj为残差向量第j个元素对应的数。
由于采用了验后残差向量,所以载波和伪距观测值的抗差因子均可采用上式进行求解。
引入构造的该抗差因子在增益矩阵中,从而实现对观测权矩阵的降权,一般选用三线段降权函数IGGIII:
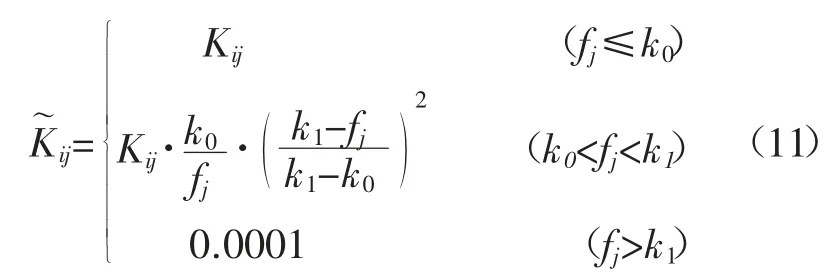
上式中,为了保证矩阵的正常求逆,所以不能将对应的观测权矩阵设置为0,只需设置为1个较小的数值即可。
4 实验分析
数据采用GMSD跟踪站2018年9月2日的双频观测数据,采样间隔是30 s,采样时长是2 h。精密星历、钟差和地球自传改正参数等产品均来自于IGS和iGMAS分析中心。同时采用IGS网站提供的对应观测历元的测站坐标作为参考值,用于对比算法的有效性。为验证基于残差的抗差因子对于载波和伪距观测粗差的抗差效果,分别采用以下方案进行数据处理:
1)方案1:标准卡尔曼滤波,不加入粗差。
2)方案2:标准卡尔曼滤波,载波加入1周粗差。
3)方案3:标准卡尔曼滤波,伪距加入10 m粗差。
4)方案4:标准卡尔曼滤波,伪距加入10 m粗差和载波加入1周粗差。
5)方案5:抗差卡尔曼滤波,载波加入1周粗差。
6)方案6:抗差卡尔曼滤波,伪距加入10 m粗差。
7)方案7:抗差卡尔曼滤波,伪距加入10 m粗差和载波加入1周粗差。
为验证算法的有效性,在原始观测数据第100历元位置人为地加入以上方案的对应观测粗差,抗差Kalman滤波不同方案结果见表1。

表1 抗差Kalman滤波不同方案结果
从表1可以明显地看出,采用标准卡尔曼滤波模型,伪距10 m的粗差对该历元定位结果影响可以忽略不计,主要是由于其观测噪声较大,赋予的权值较小,所以对最终定位结果影响较小;相反,载波1周的粗差对定位结果影响较大,主要是由于载波观测权值较大。另外,采用此抗差卡尔曼滤波模型进行数据处理,不论是观测噪声较大的伪距观测值,还是观测噪声较小的载波观测值,均能够对粗差进行较好的处理,与无粗差结果相比,其偏差均在1~2 mm级别,说明基于残差向量构造的抗差卡尔曼滤波能够有效对载波和伪距粗差进行抗差,抗差Kalman滤波模型能够较好的对载波和伪距粗差进行处理。
5 结论
介绍了精密单点定位函数模型和随机模型,然后基于验后残差向量构建了精密单点定位的抗差Kalman滤波模型。最后,采用实测数据对抗差算法的有效性进行了验证和分析:
1)伪距观测值的粗差对定位结果影响较小,主要是由于伪距观测值对应权值较小,而载波观测值由于权值较大,故对应的粗差对定位结果影响较大。
2)传统的抗差Kalman滤波对不等精度观测值抗差效果较差,基于验后残差向量构造了统一的抗差因子和观测权阵,并采用迭代算法克服残差相关性的影响,可大大减弱粗差对定位结果的影响。实验结果表明,本文抗差Kalman滤波得到的定位结果与无粗差条件下解算的定位结果之间的差值可忽略不计。
