层状半导体MoSe2/WSe2热学性能参数定量分析*
2020-03-25杨学弦黄勇刚王小云彭金璋
彭 春,杨学弦,黄勇刚,王小云,彭金璋
(吉首大学物理与机电工程学院,湖南 吉首 416000)
作为石墨烯的半导体替代品,过渡金属二硫族化物 (TMDs,如 MoS2,WS2,MoSe2,WSe2等) 在力学、热学和光电子学等领域有广泛的应用,如用于制作场效应晶体管、超低导热器件和太阳能电池转换器等.众所周知,器件性能会受周围环境温度的影响,当TMDs器件所处环境的温度较低时,材料本身的热属性将异于常温条件,热膨胀系数、晶格常数和热应变等热学参量变成温度的函数而不再是常量.这一低温因素对TMDs的应用产生了严峻的挑战,因此确定TMDs在不同温度下的热学参数(如热膨胀系数、晶格常数和热应变等)是非常重要的.
1 研究现状
二硫族化物的通式为MT2,其中M是元素周期表中IVB、VB或VIB族的过渡金属原子,T是硫族元素,即硫、硒或碲[1].层状的TMDs(图1)由单层的MT2堆垛而成.单层MT2的结构是[2]:一个单原子层Mo/W夹在2个单原子的Se层之间,通过共价键连接,Mo/W位于6个Se原子组成的三棱柱的中心.
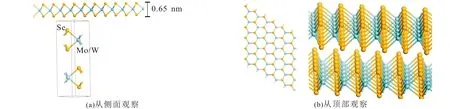
图1 MoSe2/WSe2的晶体结构
层状半导体材料MoSe2和WSe2的间接带隙分别为~1.1,~1.21 eV,在实际应用过程中表现出可调谐的带隙,可以从晶体中的间接带隙过渡到单层纳米薄片中的直接带隙,因此MoSe2和WSe2具有不同寻常的电子和光学性质,可用于制作新颖的光电器件[3-4].对MoSe2超薄纳米薄片的研究[2]表明,室温下其迁移率约为50 cm2/(V·s);当温度降低到78 K时,迁移率增加约4倍.因此,TMDs光电器件中的热管理是至关重要的.材料对温度的响应主要表现在不同的比热容、热膨胀系数等方面.比热容表征材料从周围环境中吸收热量的能力.热膨胀系数表征材料在温度变化时的胀缩现象,热膨胀系数的大小直接与材料的热稳定性相关.例如,在基板上生长层状样品时,基板与样品之间热膨胀系数的错配会导致界面产生残余应力,且在退火过程中伴随有热应力产生,从而影响器件的性能.2015年,Ding等[5]获得了常温下块体TMDs的层内热膨胀系数,MoS2,MoSe2,WS2,WSe2的分别为6.6,6.4,-1.5,5.5 MK-1.目前,热膨胀系数常采用密度泛函微扰理论(Density Functional Perturbation Theory,DFPT)[6]并结合准简谐近似(Quasiharmonic Approximation,QHA)[5]进行估算:
高温下,比热容符合杜隆柏替定律,即CV=3R(R为理想气体常数);化合物比热容遵循柯普定律,即CV=∑niCi.块体材料的德拜温度(θD)主要通过如下林达曼(Lindermann)等式[7]进行计算:
其中:Tm为熔点;A为平均原子量;ρ为材料的平均密度.密度泛函微扰理论模型计算复杂或难以得到精确数值,不便于合金材料的热学性能分析.
材料快速冷却时,表面降温快、收缩多,内部降温慢、收缩少,材料各区域的收缩程度不同,形成热应力;而材料受热时,其内部原子、分子、离子的相对位置和距离会产生变化,引起热应变.任何积累的热应力/应变都会降低器件的性能,甚至损坏器件.TMDs的热应变与温度的关联性是研究其电子器件性能的重要依据.El-Mahalawy等[8]利用二阶多项式xt=x0+x1t+x2t2,计算了TMDs在室温上升到1 000 K时的晶格常数,并给出了最小二乘拟合实验值.
笔者将利用键弛豫理论和局域键平均(Local Bond Average,LBA)近似方法研究层状半导体材料MoSe2和WSe2在不同温度下的热学性能参量,并建立热膨胀系数、晶格常数、热应变与温度的函数关系式.
2 理论计算
2.1 局域键平均近似
LBA近似方法[9]:任何可测宏观物理量与其化学键之间可通过化学参量联系起来.对于给定的样品,无论是晶体还是非晶体,在不同的外界条件下,只要不发生相变,其化学键属性和总数就保持不变.因此,可以通过关注化学键长和键能对外界环境的响应,来探讨外界环境对材料性能的影响.
2.2 键弛豫理论

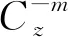

表1 MoSe2和WSe2的原子结合能和晶格常数
2.3 热膨胀系数与温度的关联性
根据LBA近似理论并结合热膨胀系数α(t)的定义[9]可得,
其中:l0为初始键长;F(r)为离开平衡位置r处的回复力;du/dl=-F(r)>0(负号表示受力方向);du/dt=CV(t/θD);u为双原子势.F(r)与平衡位置的距离呈线性关系,即-l0F(r)=A1(r)ECoh(0).其中:ECoh(0)表示0 K时的原子结合能;A1(r)为刚性因子,即仅与物质属性和结构有关的无量纲常数.于是,热膨胀系数与温度的函数关系式可简化为
(1)
其中
(2)
德拜比热模型中,
(3)
其中N为原子数,KB为波尔兹曼常数.结合(1)~(3)式可知,参数δ(r)与结合能呈反比,当δ(r)增大时,热膨胀系数-温度曲线的转折点上移,使得低温下的热膨胀系数曲线的斜率增加,高温下的热膨胀系数增大;当材料的德拜温度增大时,热膨胀系数-温度曲线的拐点右移,低温下热膨胀系数曲线的斜率减小.
根据热膨胀系数的定义,可得晶格常数与温度的关系式
(4)
将块体MoSe2和WSe2的结合能、晶格常数作为已知量,结合(1)和(4)式,得到MoSe2和WSe2的德拜温度分别为276,260 K.再将德拜温度作为已知量,通过(1)式分别与MoSe2实验测量值[8]、WSe2实验测量值[14]相互匹配,可得块体MoSe2和WSe2在不同温度下的热膨胀系数(图2),同时得到δ(r)(MoSe2)=0.033 0,δ(r)(WSe2)=0.043 2;通过(4)式分别与MoSe2实验测量值[8]、WSe2实验测量值[15]相互匹配,可得块体MoSe2和WSe2晶格常数的温度效应(图3).

图2 块体实验值与理论模型拟合CTE曲线
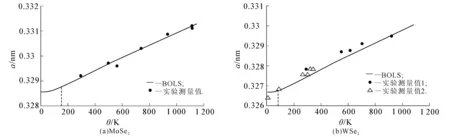
图3 晶格常数的温度效应变化曲线
从图2可以看出,当温度低于300 K时,热膨胀系数不再是常量,而是随着温度的降低而减小.从图3可以看出,当温度高于材料的德拜温度的1/3时,晶格常数呈线性伸长.利用(2)式可得刚性因子
A1(r)(MoSe2)=6.689,A1(r)(MoSe2)=4.539.
2.4 热应变与温度的关联性
从热膨胀系数与温度的关联性出发,已知初始键长l0或晶格常数a,根据热膨胀系数和热应变的定义并结合(1)式,可得
(5)
结合(4),(5)式,可预测MoSe2和WSe2在不同温度下的热应变(图4).
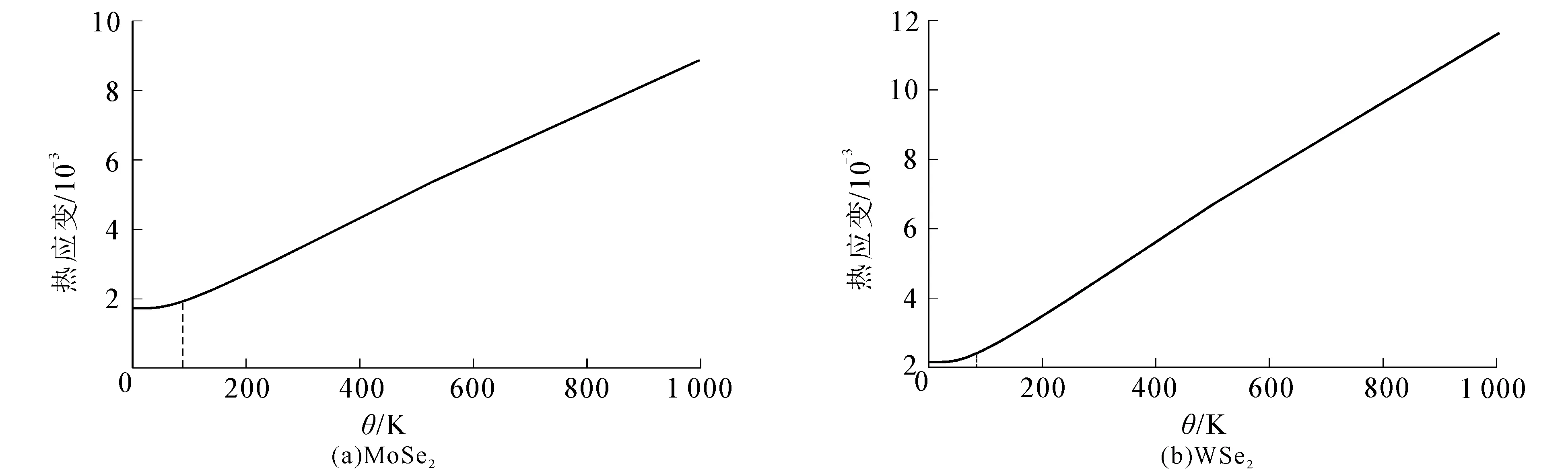
图4 热应变与温度的变化关系
从图4可以看出:当温度高于材料的德拜温度的1/3时,热应变与温度呈线性关系;当温度低于材料的德拜温度的1/3时,热应变与温度呈非线性关系.
3 结语
利用键弛豫理论和LBA近似方法对过渡金属MoSe2和WSe2的热学参量进行了分析,建立了热膨胀系数、晶格常数、热应变分别与温度的定量函数关系式,揭示了层状半导体材料热学参量的温度效应物理机制,并获得了块体MoSe2和WSe2的德拜温度分别为276,260 K.结果表明,热膨胀系数与德拜比热成正比,与原子结合能成反比;温度高于材料的德拜温度的1/3时,晶格常数、热应变与温度呈线性关系.键弛豫理论和LBA近似方法发展了半导体材料热学性能参数的数值算法理论,为新型半导体材料光电器件的设计提供了理论基础.在以后的研究工作中,笔者将推导不同层数/尺寸下的德拜温度、结合能、热膨胀系数与温度的函数关系式,从而分析材料的尺寸效应.
