超声振动辅助滚压参数对钛合金表面残余应力的影响

2020-03-25沈学会巩贤宏师亚龙

电加工与模具 2020年1期

苏豪，沈学会，巩贤宏，师亚龙

（齐鲁工业大学机械与汽车工程学院，山东济南250353 ）

钛合金是一种轻质高强度耐蚀结构材料，被广泛应用于航空、航天、化工、石油、电力、医疗、建筑、体育用品等领域。高强合金的主要弱点在于其疲劳强度对应力集中敏感，而钛合金对划伤、裂纹等表面缺陷更加敏感，污染、刀痕、划伤、腐蚀等表面缺陷都能导致疲劳裂纹萌生或扩展，进而造成零件疲劳断裂[1]。疲劳是一种表面敏感特性，据统计[2]，在疲劳失效中，80%以上的裂纹始于诸如切削加工刀痕、划伤、组织损伤、潜伏在表面和亚表面的缺陷造成的应力集中处，表面缺陷造成的局部应力集中值叠加在疲劳载荷上，大幅加速了裂纹的萌生并降低了疲劳寿命。一言以蔽之，表面完整性决定了构件的疲劳性能。

超声振动辅助滚压表面强化技术[3]是通过滚压工具头沿着表面法线方向给材料施加一定幅度的超声频机械振动，实现静压力和超声冲击振动协同作用于被加工材料表面，并利用金属材料在常温状态下的冷塑性特点使材料产生弹塑性变形，从而达到表面同时抛光和强化的工艺效果。该技术已被大量研究证明是可有效提高金属构件表面完整性的强化处理工艺[4-6]。超声振动辅助滚压工艺是通过材料晶粒纳米化[7-8]和位错增值[9]机理，在材料表面产生梯度硬化层。大量前期研究证明，与无振动普通滚压加工工艺相比，超声振动辅助滚压工艺效果更加显著[10-13]。比如：普通滚压强化后，螺纹根部的表面粗糙度值为Ra0.106 μm；施加21 kHz 超声振动后，其表面粗糙度值减至Ra0.051 μm[14]；与普通滚压工艺相比，增加20.4 kHz 的超声振动后，强化构件表面的硬度值提高了24%[3]。

实验测量往往只能获得被处理材料表面残余应力数值，无法准确得到沿着改性层深度方向的应力变化，更无法获得瞬态的应力分布情况。本文以Ti-6.5Al-3.5Mo-1.5Zr-0.3Si（TC11）型钛合金材料为研究对象，采用有限元分析和实验研究相结合的方法，基于与普通滚压工艺的对比，对超声振动辅助滚压强化钛合金表面残余应力场进行了分析。

1 实验装置与方法

本研究基于普通车床完成。如图1 所示，整个超声滚压强化装置由电子控制系统、冷却润滑系统、滚压刀具三部分组成。其中，电子控制系统可产生超声频率交流电信号，保证加工过程中振动频率稳定；冷却润滑系统通过一套润滑油液压系统完成加工过程中的冷却和润滑；滚压刀具从内到外有三层结构，分别是超声振子、套筒和外壳，该滚压刀具可通过刀架固定在车床上，其套筒套装于外壳内孔，可沿内孔自由滑动，且滚压工具头为球形滚珠，安装于一个滚珠座内，可在滚压过程中自由转动。

该实验装置可产生28 kHz 的振动频率，振幅范围为0～20 μm。实验选用的滚珠材料为硬度92HRA的硬质合金，工件材料的化学成分见表1，实验工艺参数见表2。实验将加工后的工件放入丙酮溶液中进行超声清洗，并用Xstress 300 应力分析仪测量工件的表面残余应力值，对每个工件测试10 个点，取平均值作为测量值。

表1 TC11 钛合金化学成分

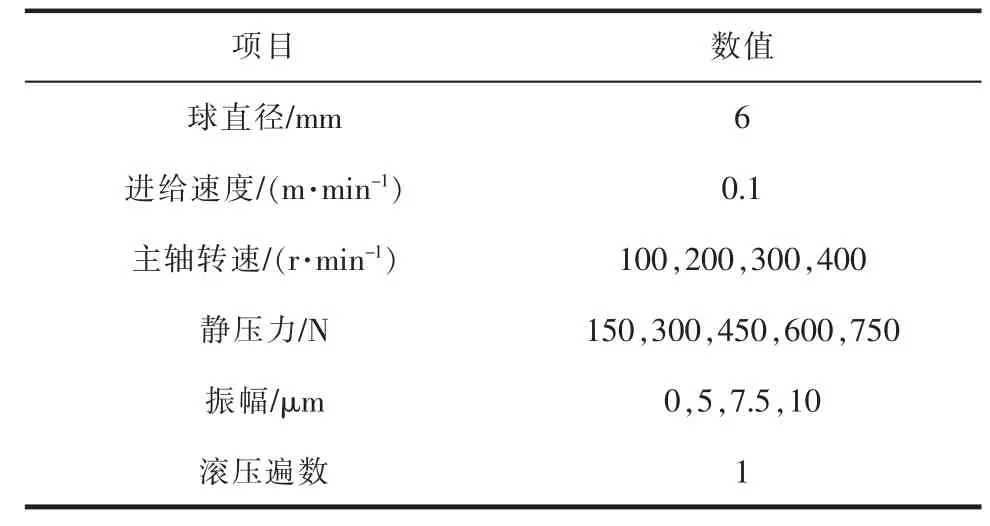
表2 工艺参数

2 有限元模型建立与分析

2.1 几何模型及网格划分

为了保证有限元分析的计算精度，实验时从工件上沿着棒料圆周加工方向提取尺寸6 mm×6 mm×3 mm 的长方体（忽略曲面曲率），以此作为有限元分析的几何模型（图2）。鉴于滚压工具头的硬度远大于工件硬度，将滚压头设为半径3 mm 的球形解析刚体；有限元模型前表面设置为对称约束表面，以便观察瞬态的应力分布结果。

工件模型采用带沙漏刚度控制的八节点线性减缩积分单元（C3D8R）来划分网格，缓解因材料塑性不可过度压缩导致的网锁问题。选择最小单元尺寸为18 μm，为兼顾计算效率逐渐向边界过渡为较粗的网格。被处理件的总单元数为143 565 个，其中细化区域单元数为25 500 个。为避免应力波边界反射对模拟结果的影响，在模型表层包覆一层半无限单元格（图2b）。

2.2 材料模型

在超声振动辅助滚压强化工艺中，被处理材料的表面层及近表面层会发生剧烈的塑性变形，材料的屈服强度也会随着应变速率的变化而变化，因此要选择可同时描述应变硬化、应变率硬化和温度软化的John－Cook 材料本构模型，其方程式为：

式中：A为材料的屈服强度；B为应变硬化常数；C为应变速率常数；n为硬化率；m为热软化常数；ε为等效塑性应变；ε*为应变速率；ε*0为参考应变速率；Tm为材料熔点温度；Tr为室温。

在强化处理工艺过程中应采用润滑油进行润滑兼顾降温。实测强化过程中的温度变化范围为30～40 ℃。忽略温度变化影响，式（1）可简化为：

材料相关力学性能参数见表3。

3 结果与讨论

如图3 所示，仿真分析结果与实验结果一致性良好，证明了仿真模型的准确性和仿真分析结果的可靠性。由图3 可看出，随着静压力增加，试样表面残余应力呈总体增大趋势。值得注意的是，与普通无振动滚压工艺相比，试样表面残余应力值随着静压力增大的趋势在450～750 N 区间的情况比在150～450 N 区间更加明显，同时表面残余应力值在150～450 N 区间内并非是明显的压应力。

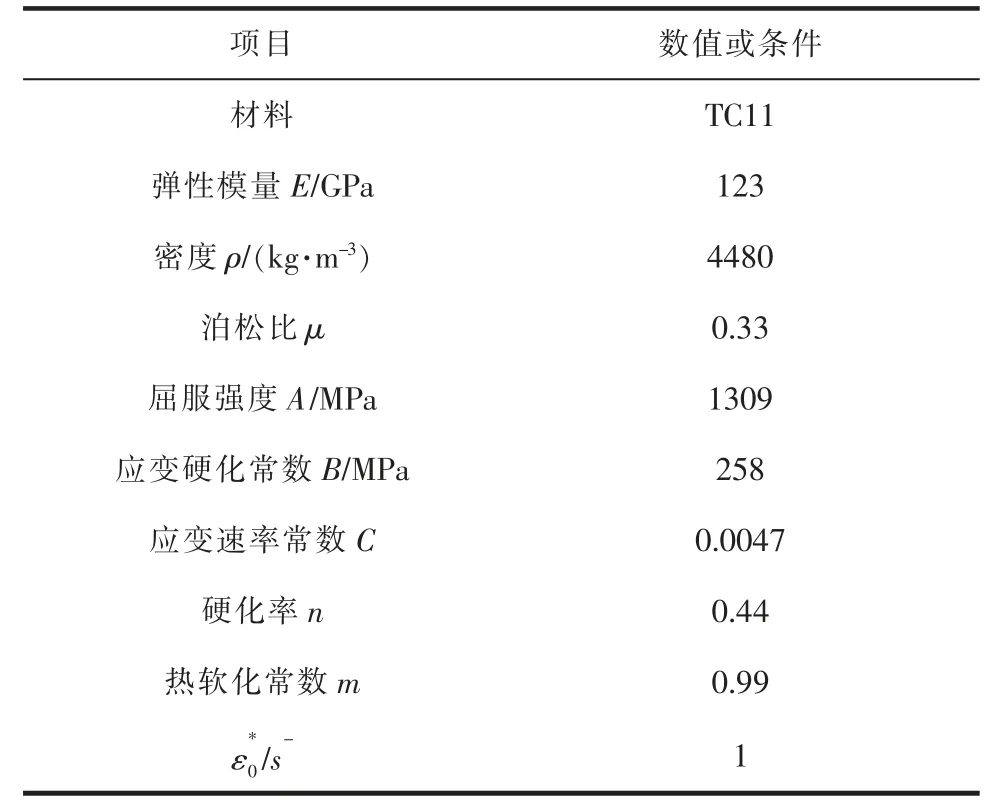
表3 材料力学性能参数表

针对该现象，可结合图4（显示两种不同工艺条件下残余应力沿深度方向的变化）和图5（显示两种不同工艺条件下材料内部的瞬态应力分布云图）分析如下：增加外激超声频率振动后，滚压头对工件表面的作用力由静压力变为高频率波动的冲击力，该力的作用形式的改变使滚压强化过程中应力波在材料内部呈振动传播，并向材料纵深不断扩散，这一方面增加了改性层的深度，另一方面也使应力值变大且最大应力没有发生在材料表面，而是发生在距离表面一定深度的近表面。如图4 所示，残余压应力值随着深度增加先增大后减小，且在距离表面约600 μm 时趋于0。

图6 是在不同静压力下，残余应力值随影响层深度的变化情况。最大残余压应力值和表面残余应力值都随着静压力的增大而显著增大；当静压力为750 N 时，最大残余压应力值比150 N 时增大了约2.5 倍；表面残余应力在150 N 静压力下表现为残余拉应力，但在750 N 静压力下则表现为-170 MPa的残余压应力。分析结果表明：在实验范围条件下，静压力是残余应力的显著影响因子之一，较大的静压力会使材料发生更剧烈的塑性变形，同时系统能量增加、残余压应力数值增大。

图7 是在不同振幅条件下，残余应力值随着影响层深度变化的情况。可见，当振幅为0 时（普通滚压），残余压应力的影响层厚度约为200 μm。而在三种振动条件下，残余压应力的影响层厚度均约为600 μm。对比三种振幅条件可知，随着振幅增加，最大残余压应力增加、残余压应力层深度减小，然而该变化趋势并不显著，经分析得知振幅对残余应力影响不显著，故在其他参数不变的条件下，单纯地改变振幅，对滚压头材料表面的冲击力影响不大。

图8 是在不同主轴转速条件下，残余应力值随着影响层深度变化的情况。可见，主轴转速对残余应力影响显著。随着主轴转速增大，最大残余压应力值明显单调增加，而最大残余压应力层深度逐渐减小，在转速400 r/min 时最大压应力值出现在材料表层而不是近表层。对该现象分析可知：在振动频率一定的条件下，主轴转速增加，单位时间内振动次数减少，材料单位面积内接受振动冲击次数也减少，由外激振动产生的振动松弛效果减弱，并表现为滚压加工过程中应力波在材料内部传播的深度减小，更多的塑性应变累积于材料表面，材料次表面更多的表现为弹性变形，因此随着转速增加，尽管最大残余压应力值增大，但影响层深度减小。