基于ISM模型的企业专利组合核心特征分析

卞秀坤，郑素丽，2，诸葛凯，张 勇

（1.中国计量大学经济与管理学院，浙江杭州 310018；2.国家质量监督检验检疫总局质量基础设施效能研究重点实验室，北京 100028）

面对从要素驱动转向创新驱动和产业结构升级为特征的经济新常态，中国知识密集型企业需要积极培育自主创新能力并做好对创新收益的保护工作。专利权赋予专利权人在一定时间内对特定技术的垄断收益以补偿研发成本，并通过限制相同信息的竞争供给使得专利权人拥有特定技术领域的竞争优势[1]。专利资产效益对依靠持续研发和技术转化而形成核心自主知识产权的知识密集型企业的作用尤其显著。随着《国家知识产权战略纲要》的深入实施，中国企业运用专利保护自身发展的能力得到强化，但对前沿技术战略的认知和应用仍存在不足。专利组合作为实施技术战略的重要方式之一已成为学术界和实业界关注的焦点，被视为复杂专利环境下技术战略分析的基本单元，但对国内企业而言仍存在认知和操作盲点。

现有研究中，学者们从专利组合理论与动因、专利组合与企业研发决策、专利组合与企业专利授权行为等多个方面进行了研究[2-4]。总体而言，目前的研究重心在专利组合的前端——专利组合的动因、行为和与之相关的决策模式上，对于专利组合特征之间的关系缺乏系统的分析。

企业构建专利组合时应从哪些特征着手分析？选取这些特征进行分析的依据是什么？这些最基本的问题亟待回答。本文依据系统工程理论中的解释结构模型分析法，内向地剖析专利组合的特征并最终构建企业专利组合核心特征的递阶模型，为企业分析和构建专利组合提供理论借鉴。

1 专利组合特征述评

经典的专利组合理论探讨了技术层面的专利组合、发明人层面的专利组合、企业层面的专利组合以及专利与市场一体化组合[5]。也有很多研究将专利组合运用到行业层面。理论界对专利组合不同情景的阐释造成实业界和初学者的困惑。本文依据国内外现有研究论述企业层面专利组合核心特征之间的关系。

Ernst[6]由技术组合的概念衍生出专利组合。Parchomovsky等[2]对企业专利组合的论述得到理论界广泛认可，定义为由一些存在明显区别又密切相关(distinct-but-related)的专利所组成的集合。PCT（Patent Cooperation Treaty, 专利合作协定）将专利组合解释为，由单个实体所拥有的专利集合体，这些专利可以是相关的甚至可以是不相关的。由此可见，专利组合最大的特点是通过对单个专利进行联结以实现协同效应[7]。知识密集型企业技术战略的制定要依靠专利基础，专利组合分析可用于评估企业的专利申请活动和创新潜能，进而研判行业的研发蓝图和商业机会[3，6]。并且，依据专利组合对技术信息的量化分析有效弥补了定性方式制定技术战略的信息缺陷，可以实现研发资源的精确配置。因此，专利组合对于企业科学认识自身专利资产、竞争对手专利布局以及行业专利竞争态势均有重要价值。

后续学者基于Ernst和Wagner的论述从不同特征展开对专利组合的分析。用专利数据表示的专利组合特征可以分为两大类，第一类是显性特征，显性特征是对可得专利指标数据的初步统计，包括权利要求数量、专利引证情况、专利组合规模和技术范围等等[8]。Blind等[9]认为企业专利申请的战略动机会影响专利组合的规模和引用特征，积极的技术战略有助于扩大企业专利组合规模。Lin等[7]的实证结果表明专利组合的平均权利要求项与企业绩效正相关。第二类是隐性特征，通过对显性特征按照一定规则二次变换所得，包括专利组合多样性、专利组合价值和专利组合一致性等[7，10]。专利组合不是专利的简单堆叠，具有结构性和系统性。隐性特征是对显性特征的延伸便于表达更为复杂隐晦的组合特质。其次隐性特征有助于理论对接，以实现对局限性解读的客观参照。学者最为关注的专利组合多样性特征与专利对应IPC（international patent classification）的分布情况有关[11]，专利对应IPC分布越分散则专利组合多样性越高。Lin等[7]将专利组合多样性可以进一步分为广义多样性和狭义多样性，结合能力观理论提供了企业多元发展或聚焦发展的整合型框架，并且可以利用专利组合的熵、一致性和可拓展性的数据可视化企业的技术发展路径[10]。

国内学者刘林青等[1]以综述的形式介绍了Wagner的专利组合理论，详细分析了专利竞争优势的多租金性质，明确指出从专利竞争发展到专利组合竞争的必然性。根据专利关联度生成的组合图谱以及全面专利组合管理的分析框架都对企业专利组合的构建和管理提供了借鉴[12-13]。陈琼娣[14]进一步实证分析了国外清洁技术企业专利组合的构建过程和应用模式。由此可见，国内学者紧跟国外研究进展介绍了专利组合的概念、分析框架、组建方法和案例研讨，但比较缺乏对专利组合特征之间关系的实证分析。

总体而言，学术界单独围绕专利组合特征展开论述的文章相对较少，更多的文章是基于Ernst和Wagner对专利组合的论述展开的应用研究。Ernst等[3]关注专利组合对技术机会预测、技术战略制定的决策作用，强调专利组合形成的技术位势、技术分布以及逐渐逼近组合真实价值的指标设计；Parchomovsky等[2]认为规模和多样性是专利组合最重要的两个特征，尤其强调规模是形成专利组合其他特征的基础。相应形成专利组合研究的两大分支，将专利组合用于技术机会和技术演变分析的应用性研究和阐释专利组合重要特征与企业绩效作用关系的机理性研究，但两大分支的研究均未足够关注专利组合多种特征之间的层次关系和逻辑联系，而理顺专利组合特征之间的结构关系是开展专利组合实证分析的基础。国内学者的研究主要基于Ernst和Wagner成果的验证和推广，因此尤其关注专利组合的规模和多样性特征，缺乏对专利组合内源性的深入剖析或者依据中国企业的实证检验。Wagner将专利组合的优势归结为规模和多样性有其特定的产业结构因素和专利体制背景，考虑到在全球产业链分工中中国企业处在不同的分工层级和技术环境下并面临不同技术战略需求的问题，专利组合不同特征的重要程度是否具有普适性有待商榷。本文尝试构建企业专利组合核心特征的解释结构模型，厘清企业专利组合各特征的层级关系和关联结构，为中国企业分析和构建专利组合提供理论基础。

2 研究方法与研究设计

2.1 研究方法

解释结构模型（interpretative structural modeling method, ISM）是由美国系统工程理论学者Warfield提出来，以把模糊不清的思想、看法转化为直观明了且具有良好结构关系的模型[15]。具体而言，运用ISM方法将影响复杂系统的因素集合分解为若干个子因素，利用人们的实践知识和计算机的辅助找出各因素之间的相互关系，最终形成可视化的结构关系矩阵图[16]。为采用ISM方法理清当前模糊的专利组合的概念，本文设计了如下主要关键步骤：

（1）组织实施ISM小组；依托知识产权课题组的8位老师和5位涉及专利方向的研究生组建ISM小组，包含了方法技术专家、协调人和参与者三方角色。成员拥有不同的学科背景因而会持有不同的观点；

（2）围绕核心问题“企业专利组合的核心特征是什么”展开研讨交流；

（3）依据国内外现有研究成果结合研讨分析确定专利组合核心特征和测度指标；

（4）在对关键问题有了清晰认识之后，成员分别独立填写关键特征相关性问卷；

（5）根据问卷结果建立邻接矩阵和可达矩阵；

（6）分解可达矩阵并建立结构模型；

（7）根据结构模型建立解释结构模型。

2.2 确定专利组合核心特征

目前学术界单独围绕专利组合特征展开论述的文章相对较少，鉴于国内实业界对专利组合概念认知的不成熟，难以通过座谈访谈和问卷调查获得一手真实资料。本文在对国内外高引和高相关度文献分析的基础上，初步拟定与企业专利组合核心特征相关的因素清单，经过ISM小组三轮反复修改完善之后筛选出19项与企业专利组合核心特征高度相关的因素，建立编码库，见表1。

表1 企业专利组合核心特征的关键因素

表1（续）

2.3 矩阵分析和模型构建

2.3.1 绘制特征因素之间的关系导向图

关系导向图是建立邻接矩阵的依据，采用二元分析法建立行元素Fi和列元素Fj的之间的“Fi-RFj”两两作用关系。分别用字母“V”表示行元素Fi对列元素Fj有单向影响；用字母“A”表示列元素Fj对行元素Fi有单向影响；用字母“X”表示行元素Fi与列元素Fj之间相互影响；用字母“O”表示行元素Fi与列元素Fj之间没有影响。根据上述作用关系原则，形成企业专利组合核心特征之间相互关系结构，如图1所示。

图1 企业专利组合核心特征之间相互关系导向

2.3.2 建立邻接矩阵

用19×19的矩阵描述专利组合核心特征之间的逻辑关系，构建邻接矩阵A。其中aij代表矩阵A中第i行第j列的元素，表示特征因素Fi和Fj的作用关系。邻接矩阵A表示如下：A=[ aij]19×19。其中，i, j=1,2, ，19。aij=0，表示Fi对Fj没有直接影响；aij=1，表示Fi对Fj有直接影响。为保证分析结果的客观性和有效性，本文将ISM小组内成员的问卷结果对照矩阵A的赋值规则逐一比较，以ISM小组成员大多数意见为选取准则，对个别争议激烈的最终赋值进行组内充分讨论并以最终的一致意见作为最终数据，建立邻接矩阵A，如图2所示。

图2 企业专利组合核心特征的邻接矩阵

2.3.3 计算可达矩阵

得到邻接矩阵之后，用Stata14.0可以进一步得到可达矩阵，可达矩阵反映了个因素间的直接和间接关系。计算过程如下：

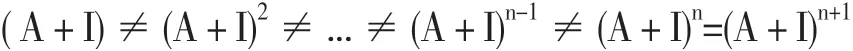
则称R=(A + I)n为可达矩阵，其中I表示单位矩阵。可达矩阵中若aij=1，则表示Fi通过直接或间接的路径可以到达Fj。计算所得n=5，由此得到可达矩阵见图3。

图3 企业专利组合核心特征的可达矩阵

2.3.4 可达矩阵层级化处理

对于每一个因素Fi，将Fi可以到达的因素汇集成一个集合，称为Fi的可达集R（Fi）；将所有能到达Fi的因素汇集成一个集合，称为Fi的前因集A（Fi）。在一个多级结构的最上一级因素中，若没有更高的级可以到达，则R（Fi）只能包含它本身和它同级的某些强链接的因素，此时R（Fi）和A（Fi）的交集对最上一级的因素来说与R（Fi）相同。即Fi为最上一级因素的条件为：R（Fi）=R（Fi）∩A（Fi）。得到最上一级因素之后在可达矩阵中去掉对应的行和列，重复以上操作得到下一层的最上一级因素。通过可达矩阵的层次化处理得到L1={5,7}，L2={1,2,3,4,6}，L3={9,10,12,16}，L4={11,13,14,15}，L5={8,17,18,19}，见表2。

表2 层级化处理后的可达集、先行集和共同集列表

2.3.5 形成解释结构模型

根据关系导向图、可达矩阵和层次分析结果构建企业专利组合核心特征的解释结构模型如图4所示。

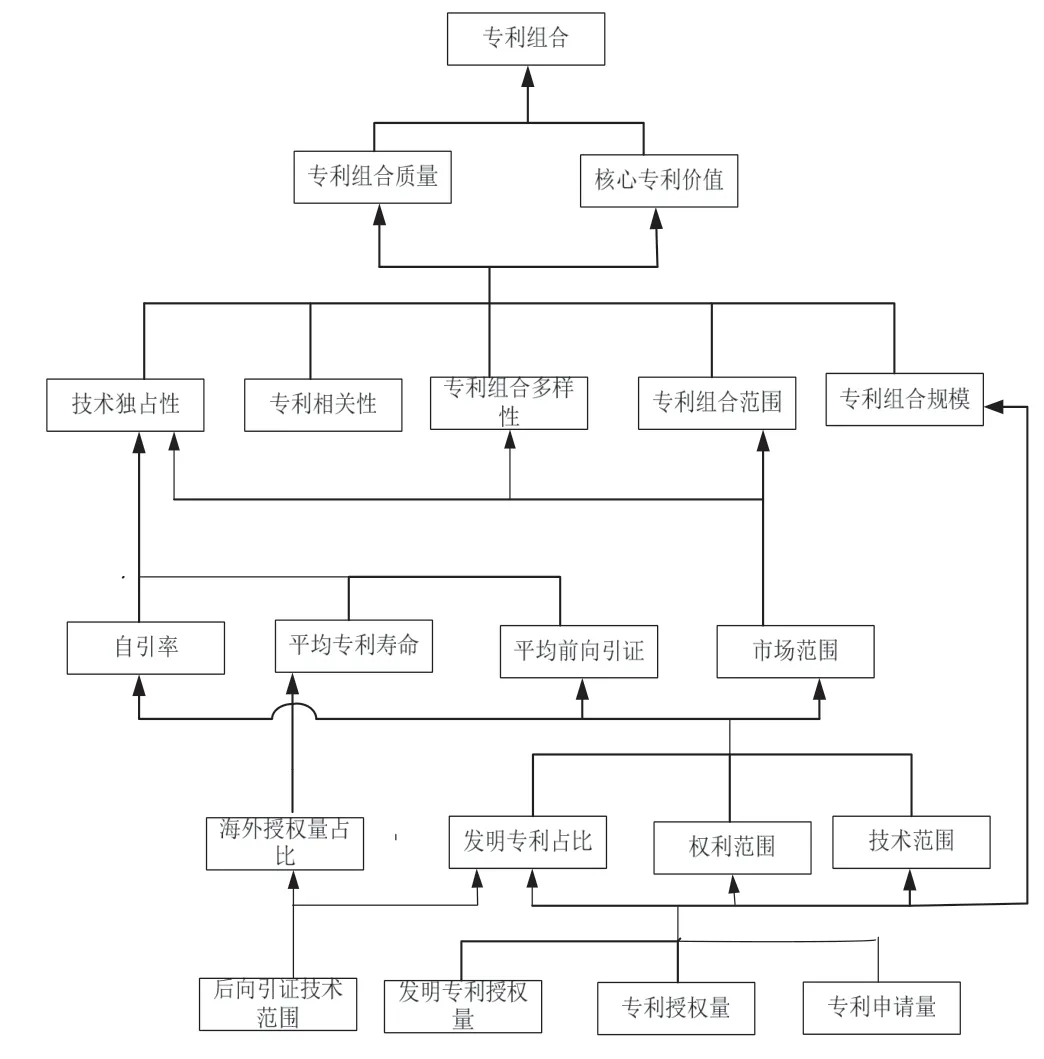
图4 企业专利组合核心特征的解释结构模型

由图4，企业专利组合的特征存在5个层级的结构关系。第五层级（专利申请量、专利授权量、发明专利授权量和后向引证技术范围）是影响企业专利组合的基础因素，这说明专利组合的规模非常重要，专利组合的所有特征几乎都需要构建在其专利数量基础之上。第四层级（海外授权量占比、发明专利占比、权利范围和技术范围）和第三层级（自引率、平均专利寿命、平均前向引证和市场范围）是影响企业专利组合的过程因素，决定了专利组合的高阶特征，属于易于量化的显性特征。第二层级（专利组合规模、专利组合范围、专利组合多样性、专利相关性和技术独占性）是影响企业专利组合的根源性因素，属于隐性特征，也是企业分析和构建专利组合时最具参考价值的维度。专利组合质量与核心专利价值是企业专利组合的重要标尺。

3 讨论与建议

本研究梳理了企业专利组合核心特征因素，并基于解释结构模型构建了因素之间的关联结构。结果表明，企业专利组合核心因素之间存在层级关系，不同因素对专利组合的影响程度和作用路径不一致。首先，专利组合质量和核心专利价值直接作用于企业专利组合，最能反映企业专利组合特征，但是尚没有公认的专利组合质量和核心专利价值的测度方法。相比之下，第二层级的特征因素（专利组合规模、专利组合范围、专利组合多样性、专利相关性和技术独占性）间接影响企业专利组合且已有确切的量化衡量方法，因此更适合作为企业构建专利组合的参考。第五层级的特征因素（专利申请量、专利授权量、发明专利授权量和后向引证技术范围）通过第四层级（海外授权量占比、发明专利占比、权利范围和技术范围）和第三层级间（自引率、平均专利寿命、平均前向引证和市场范围）接作用于第二层级的隐性特征因素，因此第五层级的特征因素起到基础性的作用，是企业专利组合形成其他特征因素的基础。由于第五层级的因素共同表示专利数量“规模”特征，因此可以判断专利组合规模的基础作用，这与现有研究结论一致。

本文的研究结果表明，企业专利组合的直接影响因素专利组合质量、核心专利价值亟需量化的衡量方法，或是以后科研人员实现突破的切入点。此外，专利组合的根源性因素（专利组合规模、专利组合范围、专利组合多样性、专利相关性和技术独占性）对企业专利组合的评估和构建具有借鉴意义，科研人员可以从这几个维度展开实证探讨。对企业而言，专利规模是实现专利组合各特征的基础条件，因此企业应注重专利布局和专利创造，同时要注重对过程因素的控制。