海上油田储采比变化规律研究
2020-03-24姚靖婕李彦来闫建丽王欣然李展峰
姚靖婕,李彦来,闫建丽,王欣然,李展峰
(1.中海油研究总院有限责任公司,北京 100028;2.中海石油(中国)有限公司天津分公司,天津 300459)
0 引 言
J油田位于渤海辽东湾北部海域L区块,主要为湖相三角洲前缘沉积,储层物性为中高孔渗,多年来陆续实施注水、注聚合物开发。目前油田处于开发中后期,含水率为88%,采出程度为30%,油田产量逐年递减。海上油田受开发投资和平台寿命的限制,投入高、开发周期短,多年来实施高速采油,导致递减率增大,储采比变化快。陆上油田对于储采比变化规律的研究较为成熟,万吉业[1]认为储采比小于12.0时油田将进入递减期;陈元千[2-3]认为油气田进入递减时的储采比约为8.0~12.0;赵明、苑丽、夏连晶[4-13]等研究了储采比与储量替代率、采出程度、递减率等因素之间的关系,并给出合理储采比计算方法。这些经验和规律主要针对陆上油田,对于海上油田储采比具有怎样的变化规律,如何指导油田可持续开发是一个迫切需要解决的问题。因此,运用油藏工程和数值模拟2种方法,结合渤海J油田实际开发生产特点,对海上油田储采比变化规律进行了深入研究。
1 储采比的定义
一般认为油田的储采比是指某年的剩余可采储量与当年实际年产量的比值。剩余可采储量是指油田技术可采储量与到某一年的累计产量之间的差值,可以取年初、年末或者年中剩余可采储量[14-16],文中采用的是年初剩余可采储量。储采比的表达式为:
(1)
式中:ω为储采比;N为剩余可采储量,104m3;NR为技术可采储量,104m3;NP为累计产油量,104m3;Q为年产油量,104m3/a。
由式(1)可知,当剩余可采储量降低时,储采比减小,当小于一定下限值时,油田难以保持稳产[10],需要寻找新的储量资源来提高油田技术可采储量,从而保证油田的可持续开采。
2 储采比与储量替代率、递减率的关系
2.1 储采比与储量替代率、递减率关系
储量替代率是指当年新增可采储量与年产油量的比值,其值越大表示储量接替情况越好。目前国际主要大石油公司的储量替代率一般为100%~150%[10,17]。
设第a年储量替代率为:
Ta=ΔN/Qa
(2)
第a-1年储采比为:
ωa-1=(NR,a-1-NP,a-1)/Qa-1
(3)
则第a年储采比为:
(4)
式中:Ta为第a年储量替代率,%;ωa为第a年储采比;ωa-1为第a-1年储采比;NR,a-1为第a-1年技术可采储量,104m3;NP,a-1为第a-1年年初累计产油量,104m3;Qa为第a年产油量,104m3/a;Qa-1为第a-1年产油量,104m3/a;ΔN为第a年新增可采储量,104m3。
将式(2)代入式(4)并整理得:
(5)
油田年递减率为:
(6)
式中:Da为油田第a年递减率,%。
将式(3)、(6)代入式(5),整理后得:
(7)
式(7)即为储采比与递减率、储量替代率的关系。
根据式(7),取稳产期末储采比为10.0,可作出进入产量递减阶段第1年递减率与同年储采比的理论图版(图1a)。由图1a可知,当储量替代率一定时,初始递减率与同年储采比呈正相关关系,初始递减率越大,则同年储采比越高。此时储采比的升高是由于递减率引起的,并非由于新增了可采储量,因此无法借此判断油田是否可以持续开发。
如果储采比保持不变,式(7)可以变形为:
(8)
当储量替代率为0时,式(8)变为:
(9)
根据式(8),取储采比为5~12,作储量替代率与进入产量递减阶段初始递减率的关系曲线(图1b)。由图1b、式(9)可知,当储量替代率为0时,要保持储采比不变,油田的产量是递减的,储采比与递减率成倒数关系,即稳产期末储采比越低,则初始递减率越高。若要提高年产量,储量替代率必须大于100%;若储量替代率小于100%,产量就会发生递减。

图1 储量替代率与产量递减率、储采比理论关系
2.2 稳产阶段储采比与储量替代率关系
如果油田处于稳产阶段,年产量基本保持不变,则Da=0,式(7)变为:
ωa=ωa-1+Ta-1
(10)
由式(10)可知:①如果油田新增可采储量等于当年产油量,则储采比保持不变;②如果新增可采储量小于当年产油量,则储采比下降,需要挖掘油田潜力,寻找新的储量资源;③如果新增可采储量大于当年产油量,则储采比上升,此时油田具备稳产的储量条件。
若储量替代率Ta为0,式(10)变为:
ωa=ωa-1-1
(11)
由式(11)可知,储量替代率为0时,稳产期储采比逐年减少1.0。如果稳产期长,则稳产期末储采比必然较低,由此导致初始递减率增大。
3 储采比与开发时间、累计产量、采出程度关系
由经验公式[18-20]可得:
lnωa=A-Blnt
(12)
lnωa=α-βlnNP
(13)
lnωa=γ-δlnR
(14)
式中:t为开发时间,a;R为采出程度,%;A、B、α、β、γ、δ为拟合系数。
由式(12)、(13)、(14)可知,储采比与开发时间、累计产量、采出程度均成双对数直线关系。随着油田不断开采,累计产油量逐渐增大,采出程度升高,储采比逐渐下降。
4 储采比与采油速度关系
运用油藏数值模拟软件Eclipse建立一个由2个反九点井网并排组成的数值模型,模型基础参数依据J油田地质油藏特征选取:注水井为2口,采油井为13口,模型网格数为61×31×20,模型地质储量为248.67×104m3,平均渗透率为1 500 mD,孔隙度为26%,原始地层压力为17.1 MPa,原油密度为0.931 g/cm3,原油黏度为26.0 mPa·s。初期采用定产油量生产,采油速度(V)变化范围为2%~10%,由此得到采收率、储采比、累计产油、稳产时间以及递减率的变化规律(表1)。由表1可知,采油速度越高,稳产期末储采比越小,初始递减率越大,稳产时间越短。由年产油量与时间关系曲线(图2a)可知,随着逐年开采,年产油量先保持稳定,后逐年递减,稳产期末储采比即为储采比下限值。采油速度越小,稳产时间越长,稳产期末储采比越高,初始递减率越小。由储采比与采油速度关系曲线(图2b)可知,储采比与采油速度在双对数条件下呈直线关系,采油速度越大,储采比越小。此外,通过数值模拟研究得到储采比和递减率的关系与经验公式(9)也是一致的。

表1 油藏数值模拟结果

图2 油藏数值模拟结果
5 矿场应用
5.1 J油田储采比变化规律分析
5.1.1 储采比与储量替代率、递减率变化规律
J油田于1999年投产,整个开发阶段中,储采比主要经历4次上升(图3):第1次是在2001年,由于年产量达到峰值后迅速递减,递减率增大导致储采比升高;第2次是2009年,油田新平台的投产以及注聚合物的实施,可采储量增加,储采比升高;第3次是2012年油田进行储量挖潜,新增可采储量,储采比再次升高;第4次则是由于2014年产油量严重递减导致的。由新增可采储量导致的储采比升高后,油田具有稳产的潜力;由递减率增大导致的储采比上升,油田无法保证稳产。最终得到J油田储采比下限值为9.4,低于9.4时,油田需要进行储量挖潜,寻找新的储量资源以保证油田可以持续开采。
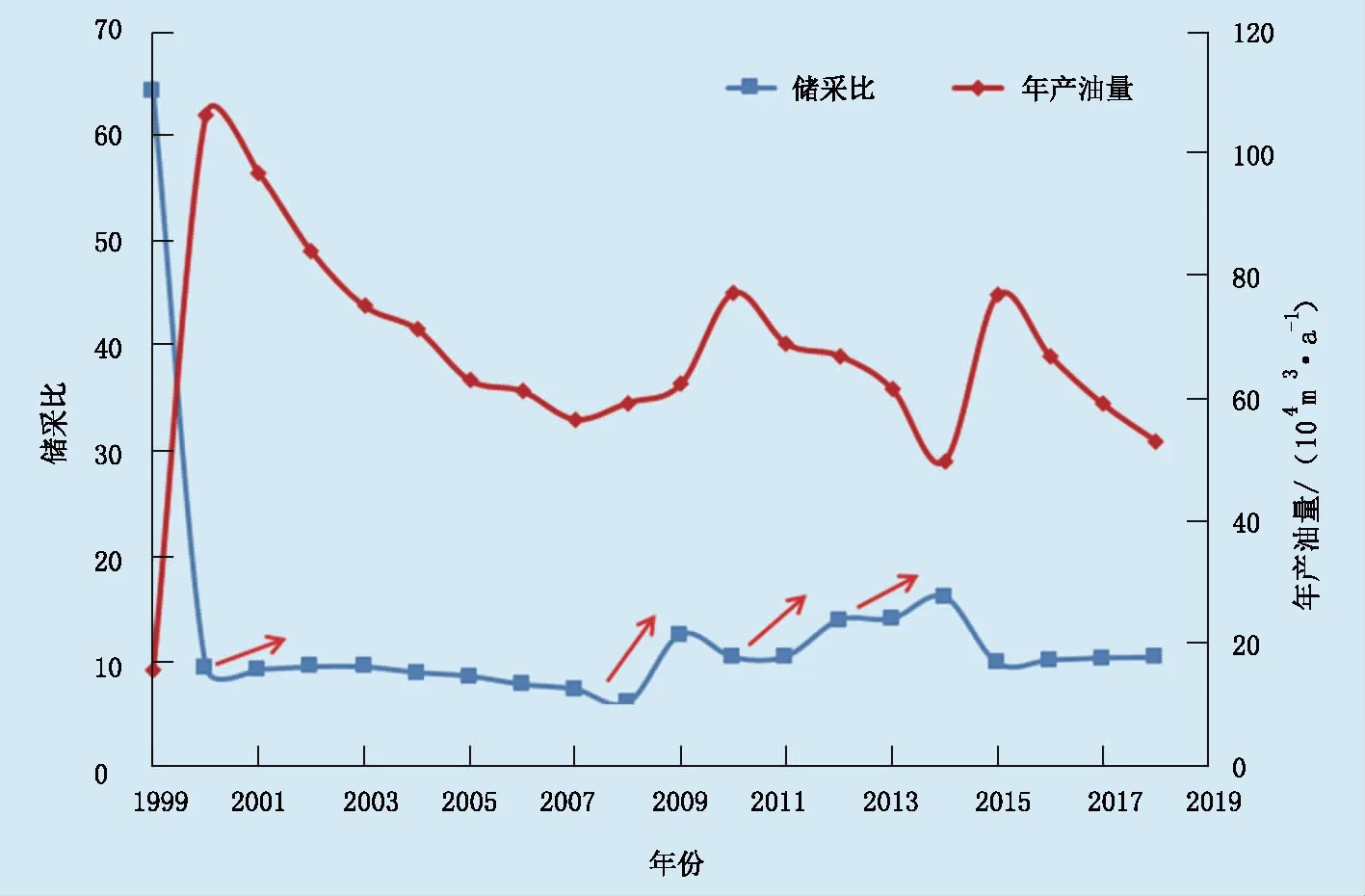
图3 J油田储采比和年产油量与时间关系
5.1.2 储采比与开发时间、累计产量、采出程度
取稳定开采阶段生产数据分别作储采比与生产时间、累计产量和采出程度关系曲线(图4)。由图4可知,储采比与生产时间、累计产量和采出程度在双对数条件下呈直线关系,随着不断开发,累计产量逐渐增加,采出程度不断升高,储采比逐渐下降,这一变化规律符合式(12)~(14)。受储量以及产量波动的影响,相关性也有所变化,当产量保持稳定的情况下,储采比与生产时间、累计产量和采出程度的相关性最好。

图4 储采比与生产时间、累计产量、采出程度变化关系
5.2 L区块储采比变化规律分析
J油田隶属于渤海L区块,优选L区块11个油田,分析储采比与采油速度、递减率之间的关系(表2)。

表2 L区块各油田储采比、采油速度和递减率统计
由表2可知,L区块各油田稳产期末储采比为4.6~10.4。由储采比与采油速度以及初始递减率关系曲线(图5)可知,采油速度越高,储采比越低(图5a);储采比越低,则初始递减率越大(图5b),符合式(9)变化规律。当储采比高于稳产期末值时油田具备稳产的潜力;反之,油田无法保证在现有储量资源的前提下继续稳产,需要深挖油田潜力,寻找新的储量资源,使油田能够持续生产。不同的油田稳产期末储采比不同,油田的挖潜时机不同。对于海上油田,储采比变化快,并不是低于8.0~12.0就一定不能稳产,各油田还需根据各自地质油藏特点得出合理的储采比下限值,这样才能更好地指导油田开发。
6 结 论
(1)通过大量数据分析和理论研究,并结合油藏工程和数值模拟方法,得到了储采比与各影响因素之间的关系。利用这些规律可以有效地分析油田实际储采比变化。
(2)稳产期末储采比越低,初始递减率越高,为保证油田持续稳定开采,需要较高的储采比。由新增可采储量引起的储采比增长,油田具备稳产潜力;由递减率增大引起的储采比增长无法保证稳产。
(3)海上油田采油速度高,储采比变化快,不能认为储采比的下限值一定在8~12的范围,需结合自身地质油藏特点切实得到符合油田生产规律的储采比,找准挖潜时机,才能指导油田高效开发。

图5 储采比与采油速度、递减率关系
