玄武岩纤维高粘沥青砂蠕变损伤模型的研究

(1.沈阳城市建设学院，辽宁 沈阳 110167；2.沈阳建筑大学 交通学院，辽宁 沈阳 110168；3.浙江大学 交通工程研究所，浙江 杭州 310058)

0 引言

沥青混合料是典型的粘弹性材料，在一定的恒定应力的作用下，粘弹性材料将产生蠕变。一个完整蠕变曲线的变化过程可分为迁移期、稳定期和破坏期3个阶段。试验中当温度较低或者所受荷载较小时，蠕变曲线往往仅表现出前两个阶段的变化特性[3]。当温度较高或是所加荷载偏大时，蠕变曲线会达到第三阶段即破坏期。Burgers模型可以很好地描述沥青混合料的蠕变试验过程的前两个阶段，但是该模型忽略了沥青混合料在初形成时存在的微裂缝和孔洞现象[4-5]，沥青混合料中的损伤是实际存在的，当蠕变达到破坏阶段时，损伤机制就会快速发展，因此现有的粘弹性模型都不能很好地描述蠕变曲线的三阶段。因此本文将Burgers模型和损伤机制进行耦合得到蠕变损伤模型，使用蠕变损伤模型对含有玄武岩纤维高粘沥青砂蠕变三阶段曲线进行拟合得到相关粘弹性参数，进而得到材料的延迟时间、松弛时间和流变时间。

1 蠕变试验

1.1 试验材料

本次蠕变试验的材料为含有玄武岩纤维的高粘沥青砂的标准小梁试件(JTG E20-2011)[6]，本试验采用的沥青是一种新型的高粘弹性沥青，该种沥青是由基质沥青、TCA添加剂、化活胶粉按照一定的比例配制而成。集料由碎石和石屑组成，其中碎石粒径分别为5～10 mm和3～5 mm各占比例为50%，石屑的粒径为0～3 mm。混合料的配合比如图1所示，玄武岩纤维掺量为0.4%(质量百分比)。蠕变试验在25 ℃条件下进行，选取无纤维的高粘沥青砂的小梁试件同时进行蠕变试验，为了使小梁试件快速达到蠕变的三阶段所加荷载为最大破坏荷载的20%，应力大小为0.33 MPa。试验仪器为砝码加载的蠕变试验机如图2所示，试件破坏如图3所示。

图1 混合料级配曲线Figure 1 Mixture gradation curve

图2 蠕变试验仪Figure 2 Creep tester

图3 破坏后的小梁试件Figure 3 Broken trabecular specimen

1.2 试验结果

蠕变曲线就是挠度随时间变化的曲线，挠度是指在变形时其轴线上各点在该点处轴线法平面内的位移量。试验得到如图4所示的蠕变曲线。

图4 挠度变化曲线Figure 4 Deflection curve

由图4可以看出无纤维试件和玄武岩纤维试件在20%的最大荷载的作用下都达到了蠕变的第三阶段即破坏期，并且从图中还可以看出含有玄武岩纤维的试件到达破坏期的时间大约在试验进行到30 min左右而无纤维试件在试验进行到大约10 min作用就已经达到了破坏期；在相同荷载相同时间的作用下无纤维试件的挠度始终大于玄武岩纤维试件。

由此可见加入玄武岩纤维的试件的稳定性要好于无纤维的试件，从试验的角度证明了纤维的加入可以大大的提高沥青混合料的抗车辙能力和疲劳寿命。

蠕变速率指的是单位时间挠度的变化情况，即为蠕变曲线的斜率，因此蠕变速率也可分为3个阶段。使用Origin8软件对得到的试验数据进行处理可以得到蠕变速率曲线如图5所示，从图5中可以很明显的得到无纤维的蠕变速率始终大于玄武岩纤维的蠕变速率。同时两种试件的蠕变速率曲线都可以分为3个阶段；第一阶段蠕变速率随时间的变化而减小，第二阶段蠕变速率基本保持不变，第三阶段蠕变速率随时间的变化而增加阶段。

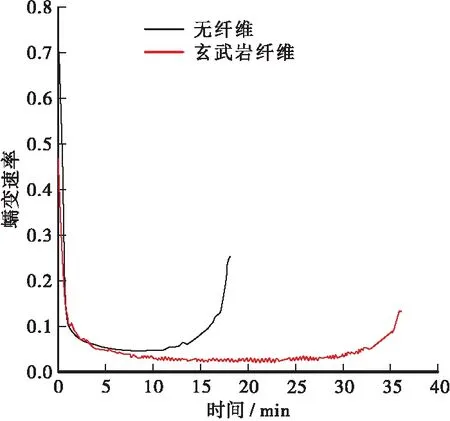
图5 挠度的变化率Figure 5 Change rate of deflection

2 蠕变损伤模型的构建

2.1 Kachanov损伤模型

经典的损伤力学理论认为材料在初步成型的过程中就存在诸如微裂纹、微空隙等微损伤。对于沥青混合料的蠕变试验来说，当荷载较小或温度较低时损伤的演化趋于稳定，但是当荷载变大或温度升高时，沥青混合料的蠕变达到破坏期时损伤机制则会快速发展[5-6]。

由材料损伤力学可知损伤因子D可以表示为：

(1)

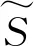
(2)

式中:σ为名义应力。

当应用损伤力学方法研究沥青混合料的蠕变性能时，需要使用合适的损伤变量，对于沥青混合料的蠕变，可以采用Kachanov蠕变损伤模型[7],

(3)

式中:C，v是基于温度的材料参数，将上式积分可得：

tr=[C(v+1)σv]-1

(4)

式中：tr表示蠕变损伤的破坏时间。

由以上两式可以得到：

(5)

2.2 Burgers模型

将Maxwell模型和Kelvin模型进行串联可以得到Burgers模型，这种模型可以很好地描述沥青混合料的蠕变松弛行为[8]。Burgers模型如图6所示。

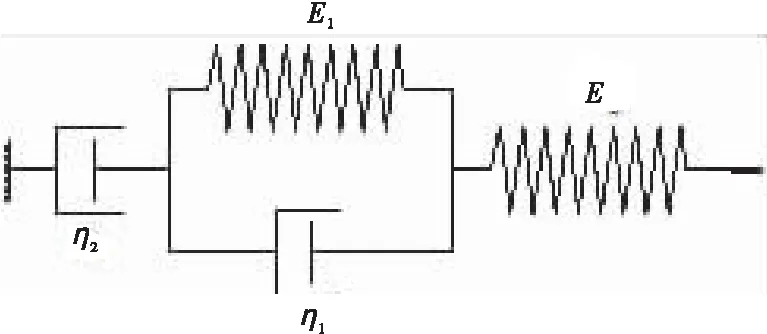
图6 Burgers模型Figure 6 Burgers model

当给材料输入恒定应力σ0时，则蠕变方程如式(6)所示：

(6)

式中:λ=E2/η2。

2.3 蠕变损伤模型

沥青混合料的蠕变试验过程中，硬化和损伤两种现象是同时存在的[5]。只考虑期中某一个因素都不能很好的表征沥青混合料的蠕变三阶段。因此需要将二者的作用机制综合考虑构建沥青混合料蠕变损伤模型。

将Kachanov损伤模型与Burgers模型进行耦合得到基于损伤力学的Burgers模型。即将式(5)代入式(2)后再代入式(6)中可以得到蠕变损伤模型的方程如式(7)所示。

(7)

式中:σ0表示应力常数;tr表示材料蠕变破坏损伤的临界时间，是材料的本身属性;v是与温度有关的材料常数;E1、E2、η1、η2是材料的粘弹性参数[9]。

2.4 蠕变损伤模型参数的确定及粘弹性特性的分析

2.4.1蠕变损伤模型参数的确定

使用1stOP软件对试验的数据进行拟合，拟合的方法选择麦夸特(Levenberg-Marquardt) + 通用全局优化法，可以得到如图7和图8所示的拟合结果。

图7 玄武岩纤维Figure 7 Basalt fibers

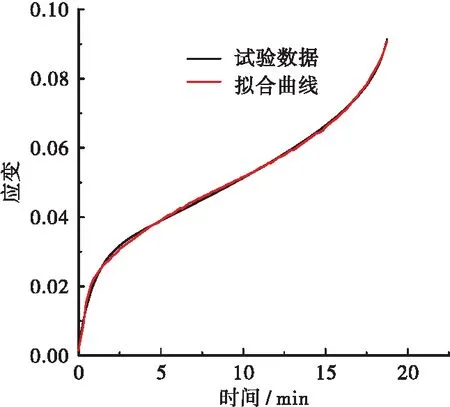
图8 无纤维Figure 8 Fiberless

从图7和图8可以看出拟合的结果和试验的结果具有很好的相关性，根据拟合结果得到二者的拟合度可达到0.99以上。

由此可以得到两种沥青混合料基于Burges蠕变损伤模型的模型参数，如表1所示。

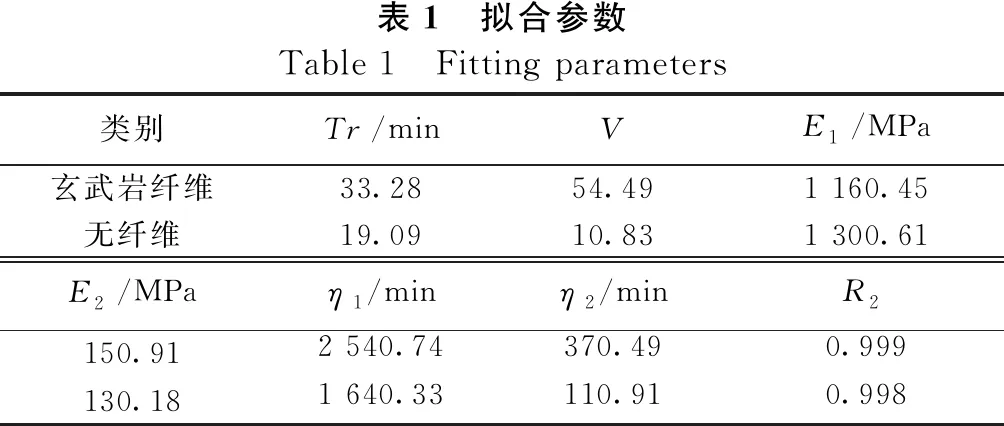
表1 拟合参数Table 1 Fitting parameters类别Tr/minVE1/MPa玄武岩纤维33.2854.491 160.45无纤维19.0910.831 300.61E2/MPaη1/minη2/minR2150.912 540.74370.490.999130.181 640.33110.910.998

2.4.2粘弹性特性分析

根据Burgers的本构模型可得E1值的大小影响沥青混合料抵抗弹性变形的能力[9]，图中两种纤维的值接近，无纤维试件的值略大于玄武岩纤维试件。η2的值可以表征沥青混合料抵抗粘性流动变形的能力，图中所示玄武岩纤维试件的值要明显有大于无纤维试件的值，则可知玄武岩纤维的加入可以减小沥青混合料产生的永久变形，增强沥青混合料的抗车辙变形的能力。

根据表1中的数据，可以得到得到两种沥青混合料的蠕变松弛时间和延迟时间，期中松弛时间表示为η1/E1，延迟时间表示为η2/E2[10]，结果如表2所示。

表2 松弛时间和延迟时间Table 2 Relaxation time and delay time类别松弛时间/s延迟时间/s玄武岩纤维131.22141无纤维75.4852.38

延迟时间和松弛时间都是材料参数，延迟时间越短，材料越接近弹性变形的特性[11]。松弛时间表示材料应力松弛的能力，在相同的观测时间内，松弛时间比较长的材料更接近粘性变形，松弛时间比较短的材料更接近弹性。由以上定义结合表2可以得到，无纤维更加接近弹性变形，玄武岩纤维更接近粘性变形。

延迟时间可以表征延迟弹性能力，延迟弹性可以直接影响沥青混合料抗车辙的变形能力。可知玄武岩纤维的加入增强了沥青混合料的延迟时间和松弛时间，同时增强了沥青混合料的抵抗弹性变形和粘性变形的能力，应力松弛的能力、延迟弹性能力。

3 结论和建议

本文通过对含有玄武岩纤维的高粘沥青砂和无纤维的高粘沥青砂进行蠕变试验，得到了蠕变三阶段曲线；使用蠕变损伤模型对试验数据进行拟合，得到两种沥青砂的拟合参数从而得到如下结论:

a.玄武岩纤维可以增强沥青混合料的稳定性。

b.将Kachanov蠕变损伤模型与Burgers模型进行耦合可以很好地描述蠕变三阶段曲线，拟合精度可达到99.8%以上。

c.玄武岩纤维试件的延迟时间和松弛时间都大于无纤维试件，因此无纤维更加接近弹性变形，玄武岩纤维更接近粘性变形，玄武岩试件的抗车辙变形能力强于无纤维试件。

d.拟合得到的流变时间与试验所得的流变时间具有很好的相关性。说明本文中所使用蠕变损伤模型对工程实践具有一定的指导意义。

e.为了验证该模型在不同温度和不同加载条件下的适用性，可进行更多加载条件和温度下的蠕变试验进行对比分析。