一种信号灯优化配时算法
2020-03-23纪祥龙苗秋凤江雪强祁华菊
纪祥龙,石 爽,曹 欢,苗秋凤,江雪强,祁华菊
(安徽三联学院 交通工程学院,合肥 230601)
1 城市交通行车道与人行道交通现状
我国经济不断发展的同时,交通拥堵现象也日益严重。交通行业这一因素在拉动国家经济发展的众多因素中起到了重要的作用,因此改善现有交通的运行状况具有重大的价值。
目前国内外学者针对单个交叉口的信号灯配时进行深入的研究,Cao[1]提出一种基于信息素的交通管理框架,用于减少交通拥堵,将动态车辆路由和交通配时策略统一起来。黄辉先[2]通过建立双目标模型来对总延误与最优速度进行双重限定。利用单片机编程、MATLAB编程控制等实现红绿灯自适应控制[3]。吴艳兰[4]综合车流量、信号灯优化配时、道路使用情况等因素建立数学模型来分析其定量的关系,来缓解交通拥堵。雷代文[5]针对不定周期信号灯配时策略的研究针对如今的信号灯配时具有较大的借鉴意义。李长光[6]综合行程时间及空间范围的特点,建立缓冲时间指数均值为目标函数,来实现时空范围的优化。卢凯[7]等通过建立基于绿信比变化的分配模型,在一定程度上缓解了交通拥堵。以上国内外研究方法均在一定程度上减少了拥堵,但也存在着考虑问题不全面等缺点。为此本研究设计了综合行人与车辆视觉盲区、交通量与行人量的信号优化配时设计。
以合肥市的金寨路与锦绣大道的交叉路口为例来说明,金寨路为横贯合肥主城区与肥西县之间经济联系的一条主动脉,而锦绣大道为金寨路绕城高速高架在从北向南方向上的主要道路分流口与大学城方向的重要通道,则该交叉路口的研究设计对于其他主要城市或者类似交叉路口具有借鉴意义。
在金寨路与锦绣大道交叉路口进行为期一个月的调研数据发现,该交叉口的畅通度较小,存在着当行人走至人行道时由于道路横截面较宽而致使行人不得不进行二次等待,从而在一定程度上限制了车辆的通行能力。该设计通过对原道路的信号配时相位借助优化算法公式进行优化配时并加入行人与驾驶员视觉盲区因素,在一定程度上提高车辆行驶的通畅度,并且提高行人、自行车等交通性质人群的出行效率。
2 交叉口的配时参数
2.1 交叉口平面图
调研路口金寨路与锦绣大道,该路口的交通情况较为复杂。金寨路南、北进口断面为四幅路,东西方向进口道分别为两幅路和三幅路,见图1。道路的横断面宽度大,金寨路路口横断面宽度为50 m、紫云路路口横断面为40 m,基本会造成行人过街需二次等待才能完成过街。且该情况下车流基本已经放完不存在放车情况,会产生空放增加出行的总延误时间。
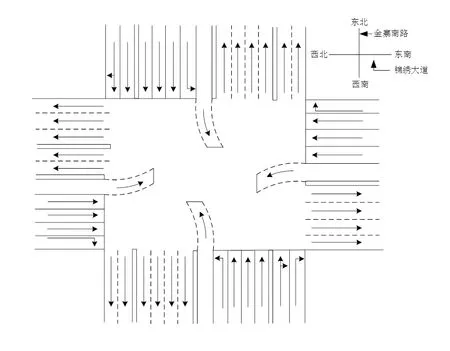
图1 交叉路口平面图
2.2 交叉口的信号参数
2.2.1信号周期
信号周期是指不同相位获得通行权循环一周所需要的时间。该典型交叉口的信号周期为129 s。交叉口的相关信号配时参数见图2、3。
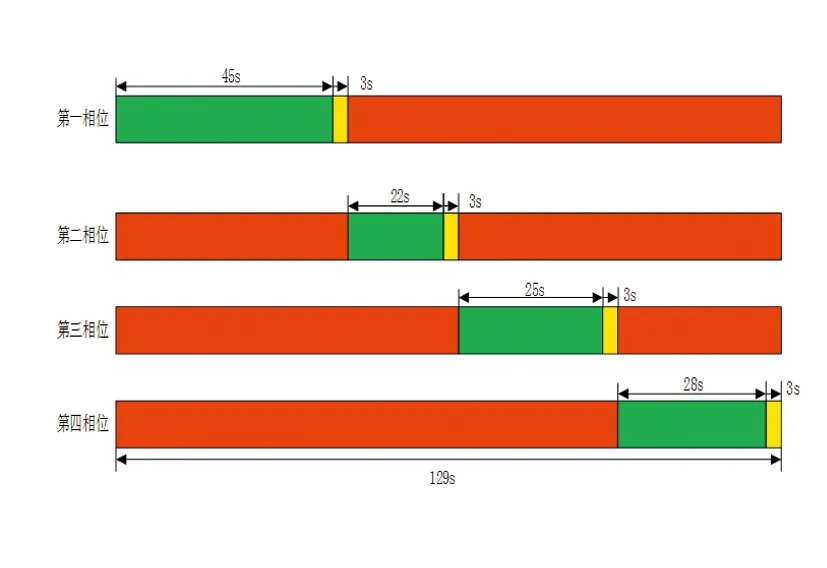
图2 相位信号配时
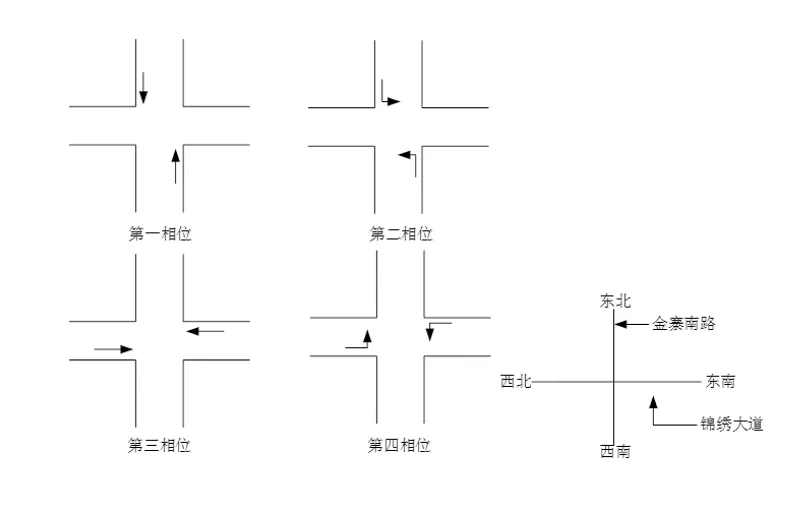
图3 道路口的相位图
经过实地调研后得出该路口每相位每辆车的停车延误与启动损耗时间为3 s,则有效绿灯时间:
Ge=g+L-A=g+3-3=g
(1)
由公式1可知该四相位的有效绿灯时间即为显示绿灯时间。可求出其绿信比分别为:
λ1=0.3489,λ2=0.1705,
λ3=0.1938,λ4=0.2171。
2.2.2饱和流量、通行能力与饱和度
针对道路宽度、坡度、大车率等因素对基本饱和流量进行修正,求其实际饱和流量如表1所示:

表1 交叉口饱和流量表 pcu/h
通过饱和流量与绿信比可以进一步求出该交叉口所在道路的通行能力:
CAPi=Si*λi
(2)
通过上述公式进行计算可得出各进口道的通行能力如表2所示:

表2 各进口道直行、左转通行能力(pcu/h)
饱和度也是反映道路通行状况的又一指标,饱和度为道路在一个小时内实际交通量与通行能力之间的比值。
调研路口各进口道直行、左转饱和度见表3。
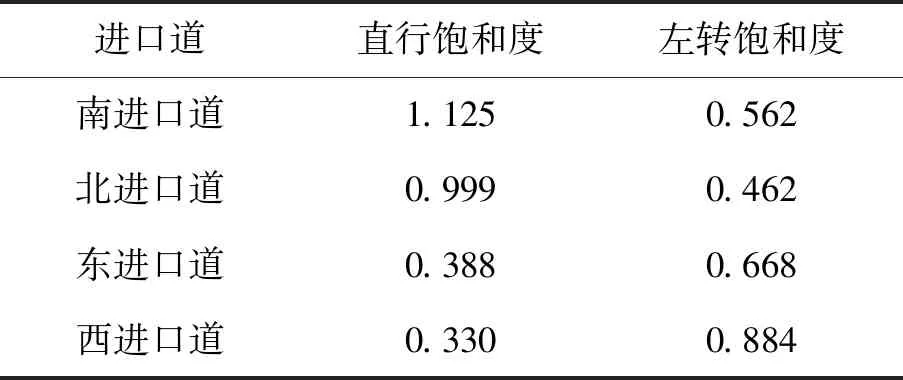
表3 各进口道直行、左转饱和度
根据以上数据我们通过延误这一指标来对该交叉口的服务水平进行评价。
D=d1+d2
(3)
经过分析与计算相关信号参数后容易知,南北进口直行方向的服务水平为F级别,南、西东进口道左转服务水平为E级别,北进口左转、西进口直行与东进口直行服务水平为D级别。
3 优化方案
3.1 交叉口停车线设计
根据图4、5可知,优化后的道路停止线在很大程度上减少了行人与车辆之间的视觉盲区,车辆停止方向与之前相比的反应时间与制动时间有了一定的加长。通过公式:
(4)
当车速一定时,制动距离一定。但当应用图4停车线时便极有可能发生交通事故;图5中的制动距离变长,则发生交通事故的概率也会随之下降。
3.2 交叉口信号配时优化设计
从上述所求相关参数知,该路口的服务水平较为低下,需要对其进行优化改进。利用韦伯斯特模型对该信号配时进行优化,最终通过延误、通行能力指标对其优化效果进行检验。
首先计算各进口车道的流率比:
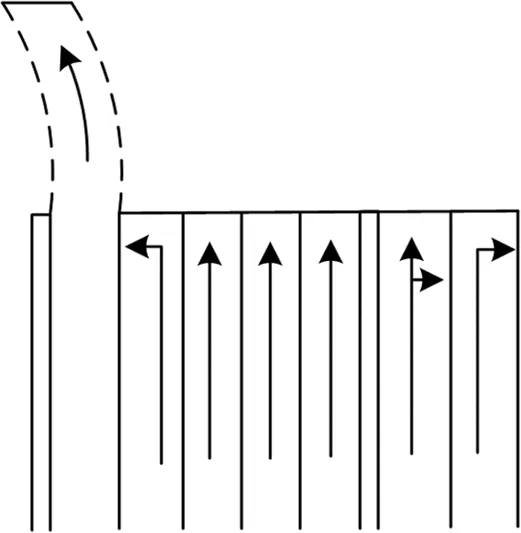
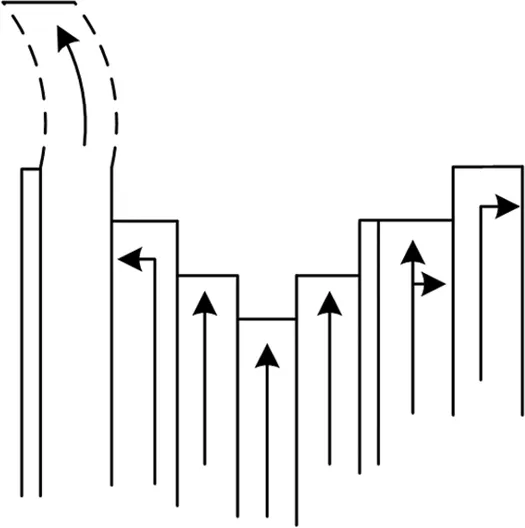
图4 道路停车线现状图

表4 各进口道流率比与主要方向的选择
由表4可知各进口道最大流率比,借助该流率比可进一步求出其最佳周期。其最佳周期与有效信号灯时长如下:
有效绿灯时间:
c1=c0-l=82-12=70(s)
南北直行绿灯时间:
南北左转绿灯时间:
东西直行绿灯时间:
东西左转绿灯时间:
又因为起动与停车延误时间与黄灯时间相同,则各相位有效绿灯时间即为绿灯显示时间。
信号配时优化后的配时参数见表5。
表5信号配时优化后的配时参数
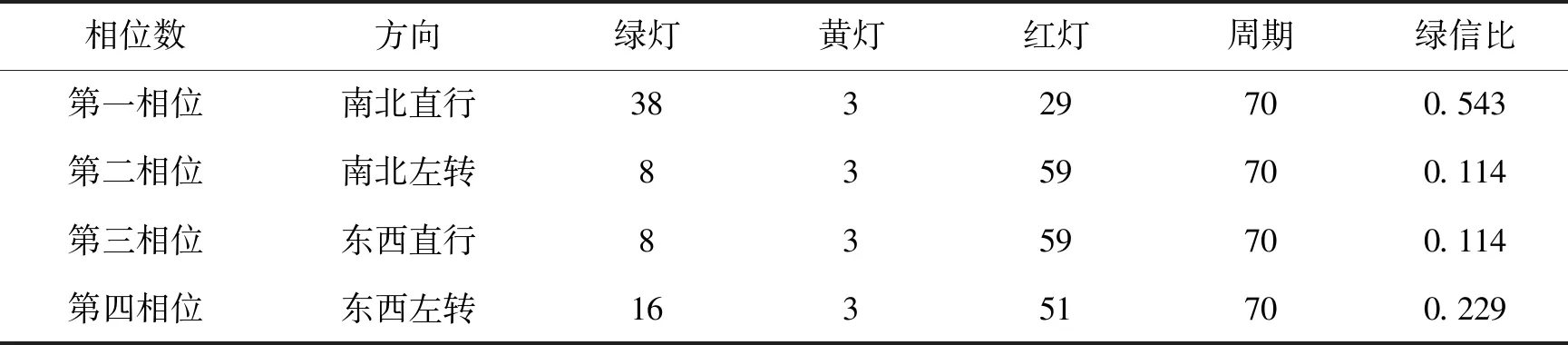
(s)
4 交叉口延误状况与评价
4.1 均衡延误计算:
根据以下公式可以计算出该交叉口不同进口道直行、左转的均衡延误指标:
各进口道直行、左转均衡延误均小于30 s,见表6。
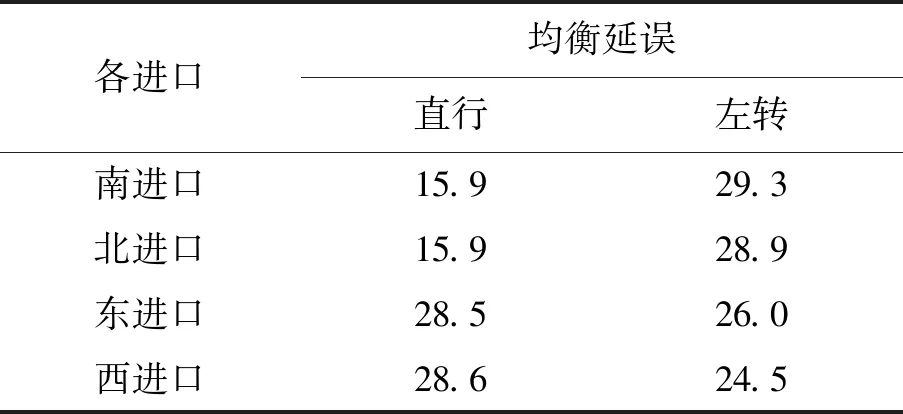
表6 各进口道直行、左转均衡延误 (s)
4.2 总延误计算与通行能力的比较
结合上述计算得到的均衡延误,以及车辆在行驶过程中所产生的运行延误这两个方面来考虑,将其视为该交叉口各进口道的总延误。并利用该交叉口的延误与通行能力作为检验优化配时的指标。计算结果列出如表7、8所示。
根据美国《通行能力手册》中对交叉口延误服务水平的标准为:
A等级:车辆延误时间≤10 s;B等级:车辆延误时间11~20 s;C等级:车辆延误时间21~35 s;D等级:车辆延误时间36~55 s; E等级:车辆延误时间56~82 s;F等级:车辆延误时间>80s。
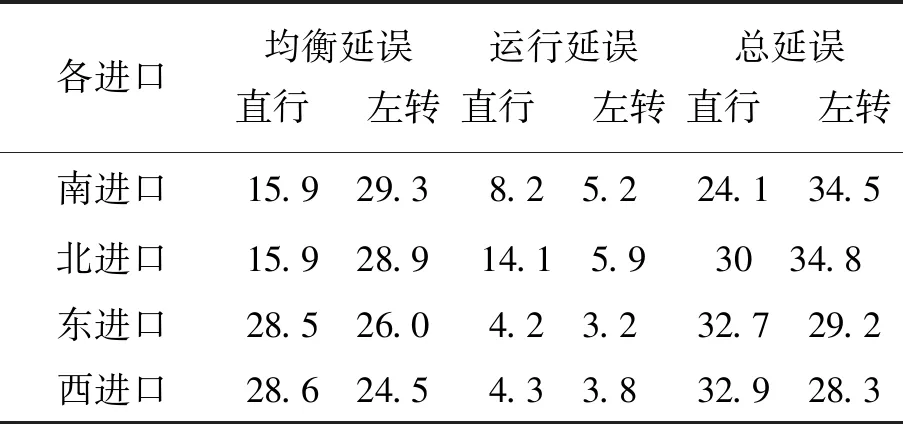
表7 各进口道直行、左转总延误 (s)
表8各进口道直行、左转通行能力 (pcu/h)
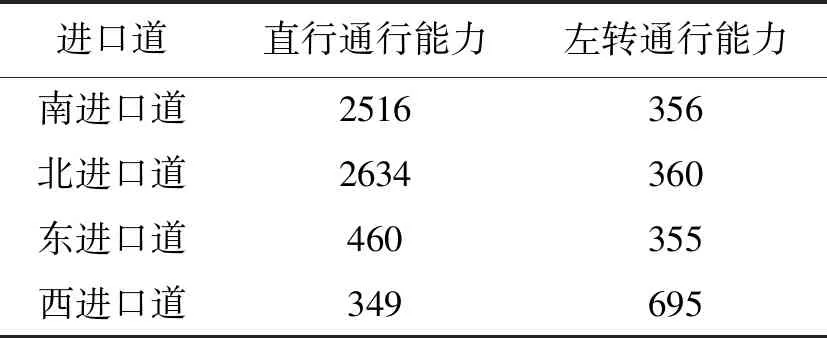
进口道直行通行能力左转通行能力南进口道2516356北进口道2634360东进口道460355西进口道349695
利用韦伯斯特算法进行优化后,通过比较延误与通行能力指标,与原信号灯比较得出优化后的信号配时与通行能力更加符合行人与交通流的定周期性变化。通过表7、8直观看出南北、东西进口道直行与左转车道的总延误均得到有效减少,且各进口道的通行能力也更加符合该典型路口的交通流波动特性。
5 研究结果
针对典型交叉口研究车辆通行能力、行人过人行横道二次过街与视野盲区问题得出以下结论:
第一,利用韦伯斯特模型结合对该交叉口数据长时间的调研、对数据采用多因素处理可以有效提高交通流获取的一般性。通过不同相位的最大流率来共同确定优化后的信号配时,进而来改变各相位的绿信比,能够更好地适应不同进口道来车率变化与行人不同的情况。
第二,该研究模型未将其它交通参与者加入,后续将针对其他交通参与者进行进一步的研究。不仅可以实现单个交叉口的时间特性优化,也从空间上对其进行优化,做到时空协调优化,是今后智慧交通发展的一大趋势。
