超高效电机采用低谐波绕组时空载铁耗研究*

孙晓波，谷汝楠，刘智慧，肖士勇

（哈尔滨理工大学荣成学院，山东 荣成 264300）

0 引言

在研制超高效电机时，需研究其对铁耗的影响并给出降耗措施。传统电机设计时，定子绕组通常采用60°相带的普通叠绕组，会产生大量谐波磁场，在转子表面产生附加损耗；而采用低谐波绕组（双层同心式不等匝绕组）会减少谐波含量［1］，降低附加损耗。此外，精确计算电机的铁耗，准确分析区域铁耗分布对提高电机效率有重要意义。

文献［2］采用等效磁路法求解了定转子齿部和轭部铁耗，但不能计算出电机的局部铁耗分布。Giorgio Bertotti［3］提出了常系数铁耗计算公式，将铁磁材料损耗分为磁滞损耗、涡流损耗和异常损耗三部分。文献［4-5］建立了场路耦合的有限元模型，对铁芯进行区域划分，得到区域铁耗分布规律。文献［6］试验对比研究了低谐波绕组（双层同心式不等匝）电机和普通绕组电机的性能。文献［7-8］提出了精细化计算铁耗的变系数模型，在磁密和频率的不同区间内该模型的主要系数取不同的值，能准确分离磁滞损耗和涡流损耗。

在考虑谐波磁场的前提下，本文以Y180M-2电机为例，对比研究低谐波绕组和普通叠绕组两种电机模型的气隙磁场的谐波含量和铁芯局部典型位置磁密的分布规律。采用变系数铁耗计算模型，结合典型位置法和路径法，对电机定转子铁耗进行精细化计算。

1 低谐波绕组理论及设计

低谐波绕组是指双层同心式不等匝绕组。采用低谐波绕组，可以在满足槽满率不变的前提下，合理调整槽内线圈的匝数，使定子电流沿铁芯表面正弦分布，产生的磁势也正弦分布，降低气隙磁场中的谐波含量，同时降低附加损耗，提高电机的效率［9］，且与普通叠绕组电机相比，只是定子绕组的排布方式和线圈匝数发生了改变，电机的其他参数均不变。

依据低谐波绕组理论，对Y180M-2异步电机的定子绕组重新设计。该电机的定子槽数Q1＝36，极对数p＝1，每极每相槽数q＝6。由于篇幅有限，本文只给出低谐波绕组电机一个极下的定子绕组分布，如表1所示。表1中的A、B、C表示A、B、C相绕组；P表示某相的正相带，N表示某相的负相带；正号（＋）表示电流流入，负号（－）表示电流流出；Z代表C相的负相带。另一个极下的X（A相的负相带）、C、Y（B相的负相带）相带绕组分布类似。

本文所设计的低谐波绕组电机的平均节距y＝12，当每相串联总匝数为48、每极每相槽数为6时，由每相带各个槽内线圈的匝数比相同，得到低谐波绕组每相带各个槽内线圈的理论匝数比为［10］：

从而，各个槽内线圈的计算匝数分别为13.71、11.83、9.60、7.07、4.33和1.46。最终确定低谐波绕组电机各个槽内线圈的实际匝数分别为14、12、9、7、4和2。

2 气隙磁密

应用Ansoft软件对低谐波绕组电机和普通叠绕组电机进行2D建模和有限元仿真。采用自适应网格剖分，仿真时间为0～0.5s，时间步长为0.000 02s。图1为两种电机的气隙磁密波形，表2为两种电机的基波和主要谐波磁密幅值。由表2可以看出，采用低谐波绕组后，气隙磁密中的基波含量减少4.26%，但主要低次谐波和一阶齿谐波（35次和37次）含量明显减少，其中3次谐波含量减少73.9%，5次谐波含量减少44.3%。

表1 低谐波绕组电机一个极下的定子绕组分布

图1 低谐波绕组电机和普通电机的气隙磁密波形

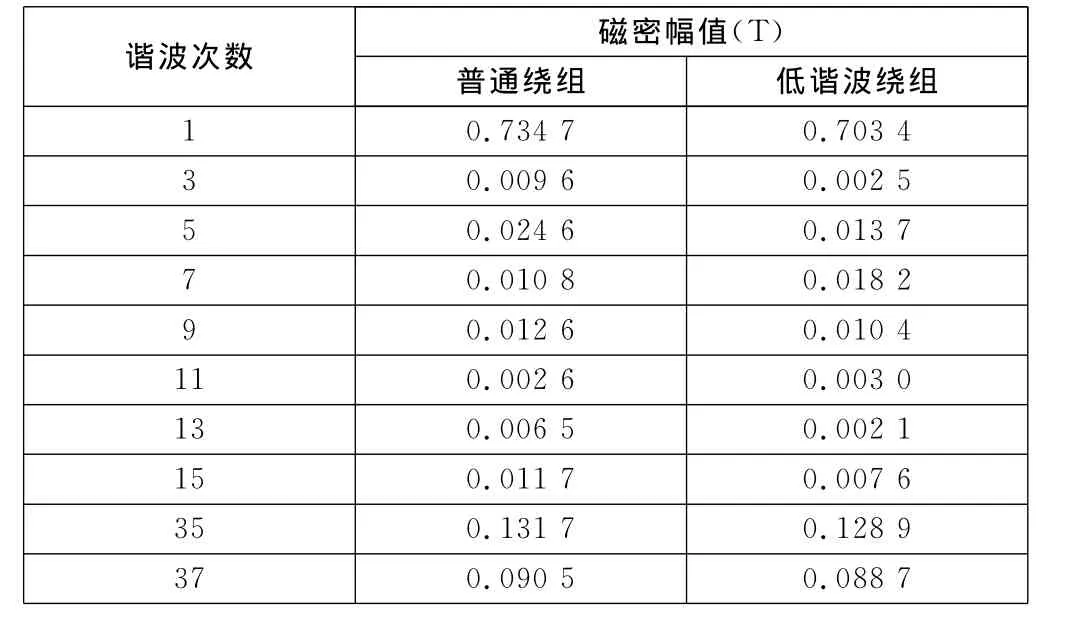
表2 两种电机气隙磁密的基波及主要谐波磁密幅值

3 电机空载铁耗计算方法

3.1 三项式常系数铁耗计算模型

文献［3］中，Giorgio Bertotti给出的三项式常系数铁耗计算模型中铁耗密度PFe的计算公式如下：

其中：kh为磁滞损耗系数；ke为涡流损耗系数；ka为异常损耗系数；B为磁密幅值，T；f为电源频率，Hz；α为磁滞损耗经验系数，一般取α＝2。

式（1）中，khfBα为磁滞损耗，kef2B2为涡流损耗，kaf1.5B1.5为 异 常 损 耗 。 异 常 损 耗 数 值 很 小 ，可 忽 略，则式（1）简化为：

3.2 两项式分段变系数铁耗计算模型

电机工作在磁化曲线的非线性段，磁导率不再是常数，用常系数铁耗模型计算铁耗误差将增大。文献［8］提出了两项式分段变系数铁耗计算模型，采用附加磁密项考虑铁磁材料饱和导致的涡流损耗和高次谐波导致的磁滞损耗。铁耗密度计算公式为：

其中：k1、k2、β1、β2均为随磁密的幅值和频率而变化的系数。

从而，电机中的总铁耗为：

其中：ρ为硅钢片的密度，ρ＝7.75×103kg／m3；lm为净铁芯长度；i为模型中的第i个单元；Ai为第i个单元的面积；n为谐波次数；Bn和fn分别为基波及各次谐波磁密的幅值和频率；k1n、β1n和k2n、β2n为变系数，随磁密幅值与频率变化，由fn和Bn决定其大小。

式（4）中，khBαnfn（k1nBnβ1n）为 磁 滞 损 耗，其 中khBαnfn为常系数模型中的磁滞损耗项，k1nBβ1nn为磁滞损耗磁密附加项；keBn2f2n（1＋k2nBnβ2n）为涡流损耗，其中keB2nf2n为常系数模型中的涡流损耗项，k2nBβ2nn为涡流损耗磁密附加项。

用两项式变系数铁耗计算公式对电机铁耗进行计算时，为了简化计算，可根据磁密幅值Bn和谐波频率fn所在的范围，参考文献［8］，由硅钢片DW470的磁滞损耗系数和涡流损耗系数（见表3）以及相应的磁密附加项系数（见表4）查出相应的系数。

表3 硅钢片DW470磁滞损耗系数和涡流损耗系数

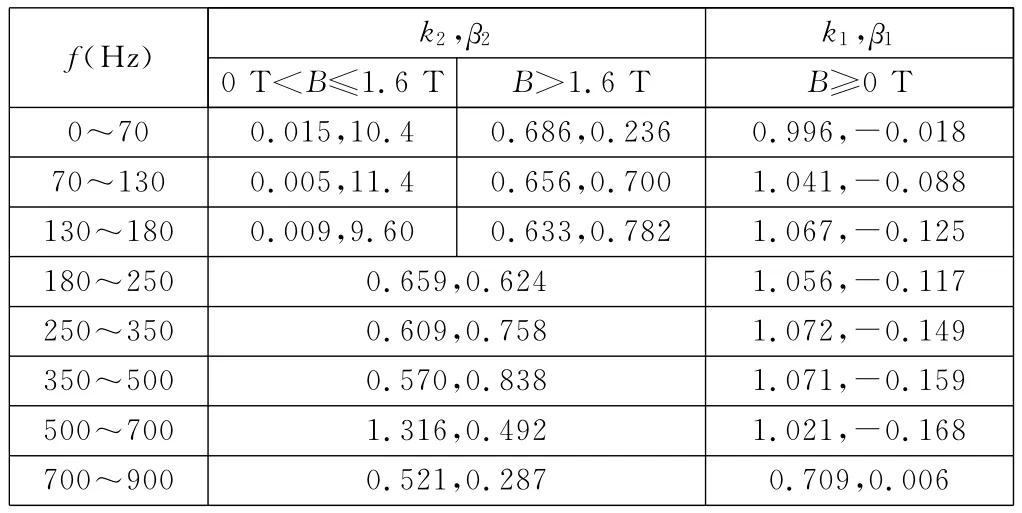
表4 硅钢片DW470的磁密附加项系数

由于其他高次谐波（一阶齿谐波除外）产生的铁耗很小，本文计算的定转子铁芯的总铁耗是指1次～18次谐波铁耗、35次和37次（一阶齿谐波）谐波铁耗和。1次～18次谐波产生的铁耗用两项式分段变系数铁耗计算模型，一阶齿谐波产生的铁耗采用两项式常系数铁耗计算模型。

3.3 低谐波绕组电机空载铁耗计算

图2为定转子相对位置关系。将定转子铁芯划分为若干个区域如图3所示，其中定子铁芯分为轭部（区域1）、齿与轭交界处（区域2）、齿身（区域3）以及齿顶（区域4）4个区域；转子铁芯分为齿上部（区域5）、齿下部（区域6）以及轭部（区域7）3个区域。

图2 定转子相对位置关系

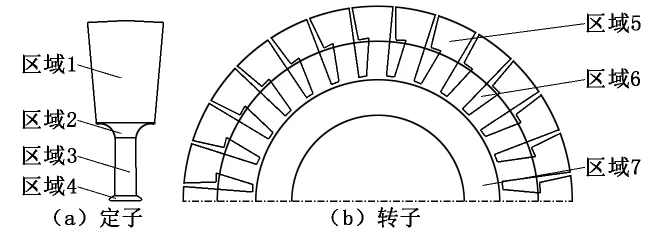
图3 定转子区域划分图

将典型位置点的磁密矢量分解为径向分量Br和切向分量Bt，则：

其中：er为该位置点的单位径向矢量；et为该位置点的单位切向矢量。

计算定子铁耗时采用典型位置法，在定子各区域内选取典型部位，如图4所示。在区域1选择5个典型位置点，T1～T5；在区域2选择3个典型位置点，E1～E3；在区域3选择4个典型位置点，S1～S4；在区域4选择3个典型位置点，D1～D3。将定子铁芯不同区域典型位置点的径向磁密和切向磁密在一个周期内的磁密波形进行傅里叶分解，得到径向磁密和切向磁密的基波及各次谐波磁密幅值，将其代入式（3）、式（4），得到所对应区域的径向铁耗和切向铁耗，求和后得到电机定子的总铁耗。

图4 定子典型位置点

计算转子铁耗时采用路径法，转子铁芯路径选取如图5所示。其中，在区域5选择4条路径，路径1～路径4；在区域6选择3条路径，路径5～路径7；在区域7选择3条路径，路径8～路径10。将转子铁心各区域内各路径的磁密波形进行傅里叶分解，得到基波及各次谐波磁密幅值，将其代入式（3）、式（4），得到所对应区域的铁耗，求和后得到电机转子的总铁耗。

4 定转子铁芯的铁耗计算结果分析

对上述定转子铁芯不同的区域，计算得到的低谐波绕组空载时区域铁耗如表5所示。

普通绕组空载时定转子铁芯各个区域铁耗的求解方法同低谐波绕组电机，其空载时的区域铁耗如表6所示。

图5 转子铁芯路径

表5 低谐波绕组定转子铁芯不同区域的铁耗

表6 普通绕组定转子铁芯不同区域的铁耗

从表5和表6可以看出：无论采用哪种绕组，定子轭部铁耗所占的百分比最大；定子铁耗从大到小依次为定子轭部、定子齿身、定子齿与轭交界处以及定子齿顶；转子铁耗从大到小依次为转子齿上部、转子齿下部以及转子轭部，且转子铁耗主要集中在转子齿上部。

表7为低谐波绕组与普通叠绕组电机铁耗的对比。由表7可以看出，与普通绕组电机相比，采用低谐波绕组后，基波铁耗减少11.1%，谐波铁耗减少22.0%，总铁耗减少14.2%。可见，采用低谐波绕组能够显著降低电机损耗，提高电机效率。

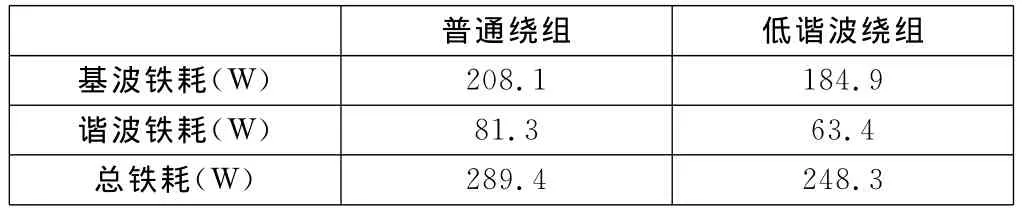
表7 低谐波绕组与普通绕组电机铁耗对比

5 结论

采用低谐波绕组后，与普通绕组相比，并没有改变定转子铁芯各部分铁耗的分布规律，定转子铁芯各部分铁耗的大小顺序不变，定子局部铁耗从大到小依次为定子轭部、定子齿身、定子齿与轭交界处、定子齿顶，转子局部铁耗从大到小依次为转子齿上部、转子齿下部、转子轭部；气隙磁密中的基波含量略有减少，但主要低次谐波和一阶齿谐波含量明显减少，其中3次谐波含量减少73.9%，5次谐波含量减少44.3%。采用低谐波绕组后，基波铁耗减少11.1%，谐波铁耗减少22.0%，总铁耗减少14.2%，有效地提高了电机效率。