玉米主产地区收入保险费率厘定问题研究
2020-03-20谷政任志宇
谷政 任志宇


摘 要:运用HP滤波法对1995—2016年玉米主产地区玉米单产和现货价格数据进行处理,通过参数法拟合玉米单产和价格序列分布,采用Copula函数构建联合分布函数,经蒙特卡洛随机抽样后得到期望收入样本,由费率厘定公式计算出主要省份收入保險保费费率。研究发现,在70%、75%、80%、85%和90%保障水平下,玉米主产地区收入保险平均费率依次为33‰、38.8‰、45.3‰、52.8‰和61.7‰;新疆、黑龙江、吉林和辽宁省4个省份的保险费率高于其他省份均值;在同等保障水平下收入保险的费率要低于种植险,在同一费率水平下,农产品收入保险提供的保障高于现行的物化成本保险。最后提出完善农产品期货市场、科学划分农业区域风险和制定收入保险保费分级补贴与双向补贴政策的建议。
关 键 词:玉米;收入保险;保险费率;费率厘定
中图分类号:F840.66 文献标识码:A 文章编号:2096-2517(2020)01-0069-12
DOI:10.16620/j.cnki.jrjy.2020.01.008
农业是国民经济不可动摇的基础,同时也是弱质产业, 其发展离不开政策性农业保险的保驾护航。2017年“中央一号”文件提出支持地方开展特色农产品保险, 探索建立农产品收入保险制度。2018年“中央一号”文件要求深化农产品收储制度和价格形成机制改革,积极探索三大粮食作物完全成本保险和收入保险试点。2019年“中央一号”文件中则明确提出,扩大主粮作物收入保险试点覆盖范围,完善收入保险经营体系,让其成为服务“三农”、实现“乡村振兴”战略的重要支撑点。从国际经验和我国的农业保险实践来看,收入保险是未来农业保险的主导产品形态,也是我国农业产业转型和农产品市场定价机制改革的重要手段[1]。农产品收入保险是以农户的收入作为保险标的,它不仅承保因自然灾害带来的产量损失[2],而且承保市场风险所造成的价格波动损失。目前我国各地实施的农业险种保障水平低下, 无法保障农户获得稳定的收入, 已不能满足现代农业风险管理的需求。随着农业产业化、 规模化和集约化经营的推进,我国农业保险势必由“保成本”转向“保收入”来满足我国农业现代化发展的现实需要。
玉米是我国第一大粮食作物,在国家粮食安全中占据着重要地位。同时,玉米集粮食、经济和饲料三种作物的身份为一体,具有多种用途,对于国民经济运行有着重要作用。中央提出农产品收入保险试点后,实践中也开始出现个别地区的玉米收入保险试点,这意味能够有效保障玉米产业稳定发展的玉米收入保险得到了政策关注并付诸了实践探索。
一、文献综述
国外农业保险起步较早,关于农产品收入保险定价的相关理论研究比较成熟。而国内研究则相对较晚,但也有学者从不同角度对农产品收入保险开始进行研究。
(一)关于产量和价格边缘分布拟合的研究
农产品收入保险的收入分布是基于农作物产量和价格分布联合构建而成,准确地估计出农户的收入分布能够有效提高保险定价的科学性和合理性。Bielza等(2002) 以西班牙橄榄油为例,通过多种分布拟合类型对橄榄油的产量和价格序列进行处理, 经AD、K-S和卡方检验发现,Logistic分布清晰地表现出农作物现货和期货价格数据尖峰厚尾特征,价格序列大多服从采用Log-Normal分布[3]。Ghosh等(2011)采用单一分布模型来估计农作物产量和价格序列,这会导致边缘分布估计存在偏差[4]。Gray(1995)通过多种分布来拟合美国威斯康星州玉米和小麦的单产及价格序列,发现Weibull和Hyperbolic secant对单产序列分布拟合效果较好,Burr、Log-logistic和Gamma对价格分布拟合效果较好[5]。
(二)关于相关性分析以及联合分布构建
Goodwin等(2008)研究发现,Copula函数能够较为精确地测算出农作物产量和价格分布之间的关联关系,在构建多个随机变量的联合分布上具有一定优势,在收入保险风险测算方面具有很好地实用价值[6]。Osama等(2015)以西班牙多个县域的农作物为例, 通过Copula方法计算农作物产量和价格的联合分布,研究发现不同区域的最优Copula模型选择有差异,最后测算出的保险费率也存在略微差异[7]。Goodwin等(2015)研究发现,Copula函数在费率厘定中的应用提高了农产品收入保险定价的科学性及合理性,在收入保险风险测算方面具有很好的实用价值[8]。Pavlista等(2012)对比分析了参数法和非参数法对农业保险费率厘定的优缺点。在运用核密度法对农产品单产序列和价格序列损失分布进行估计时会出现非对称和偏差现象,相比之下参数估计法更加灵活简便,但需要以已知的先验分布作为基础[9]。Goodwin等(2014)对农产品历史数据采用混合Copula模型进行实证分析,发现Vine-Copula模型能够更精准地估计出单产和价格的相依结构关系,这使得组合风险的估计效果更好[10]。Goodwin(2004)的研究发现,当引进一种新的保险险种时,很多历史数据都不具有参考价值,需要根据可用的产量数据和价格数据来模拟损失分布,蒙特卡洛模拟法可以基于现有的实际数据估计出农户的损失分布,这种做法有效提高了费率测算的合理性和科学性[11]。
(三)关于保费测算和定价技术研究
不少学者进行了深入分析。王克等(2014)提出在农险保单设计及定价中,Copula函数能够很好地处理随机变量拟合分布从而提升农业风险管理水平[12]。叶明华等(2018) 基于黑龙江省历年大豆单产和现货价格序列,估计得出Dagum分布对大豆现货价格分布拟合效果较好,Hyperbolic secant分布对大豆的单产数据拟合效果较好; 后经多元Copula模型构建联合分布, 最终测算出当保障水平为70%~100%时,大豆收入保险费率区间为0.9%~4.5%[13]。晁娜娜等(2017) 对新疆地区进行风险区域划分, 基于多元 Copula方法对棉花收入保险费率厘定进行研究,测算出在95%保障水平下不同风险划分区棉花收入保险的纯保险费率在4.74%~6.76%[2]。谢凤杰等(2011)基于Copula函数测算不同保障水平下纯保费费率范围,得出安徽省阜阳市大豆、玉米、小麦收入保险费率低于当地产量保险费率[14]。谢凤杰等(2017) 对辽宁省大连市县域大豆收入保险费率进行测算,得出Frank Copula模型构建黄豆单产和价格联合分布效果最好,以蒙特卡洛模拟预期收益测算出大连市、普兰店、瓦房店、金州和庄河5个区域的黄豆收入保险费率[15]。王国栋等(2019)以甘肃省苹果为研究对象,运用Copula函数和蒙特卡洛方法测算了不同保障水平下的收入保险费率[16]。冯文丽等(2017)基于河北省玉米单产和期货价格对收入保险费率厘定进行研究,选取出最优拟合函数Clayton Copula生成收入样本序列,测算出在70%~100%的保障水平下玉米收入保险的费率值为4.79%~6.80%[1]。 付慎一(2018)以吉林省玉米为研究对象,运用多元Copula模型测算吉林省各市县玉米收入保险费率,发现多元Copula模型应用于农产品收入保险定价时使得费率厘定更加精确[16]。
(四)农产品收入保险在我国的发展状况
鉴于国外收入保险成功实践经验,国内对农产品收入保险的关注度也越来越高。庹国柱等(2016)提出我国具有农产品收入保险巨大潜在需求,部分农作物已经具備开展收入保险的前提条件[17]。钟甫宁等(2004)认为农产品收入保险与我国市场化改革和政策导向机制匹配,其全面兼顾产量风险和价格风险的特性符合我国现代农户风险管理需求[18]。王宝玲等(2017)认为收入保险的开展还能够推动我国农产品市场价格机制改革。相比产量保险与价格保险,在相同保障水平下,同一农作物投保农业收入保险能给农户带来更多的经济效益[19]。汪必旺(2018)认为农产品收入保险能够改进我国政策性农业保险的运作效率[20]。
目前国内研究主要是针对区域性农作物收入保险进行定价研究[21-23],尚未有学者以玉米主产地作为研究对象测算农业保险费率。目前我国农产品收入保险处于试点运行的开展阶段,本文的研究能够为其他农作物收入保险费率厘定提供经验借鉴及技术参考。
二、数据及研究方法
农产品收入保险费率厘定研究的技术核心主要是数据滤波处理、 分布拟合选择和联合分布构建。对数据进行滤波处理去除趋势项能够获得较好的分布拟合效果,选取拟合出最优边缘分布,构建基于单产和价格最优相依参数的联合分布。以上处理可以有效降低农产品收入保险定价的基差风险,有效提高保费厘定的科学性。
(一)数据来源
农产品中玉米集粮食、经济和饲料三种作物身份为一体,对产业链上下游经济影响显著,故本文选取玉米作为农产品收入保险费率测算对象。玉米价格数据选取主要省份1995—2016年(共22期)平均50公斤出售价格年度数据来表示,玉米单位面积产量(公斤/公顷)数据时间区间与价格保持一致,选取各个省份历年单产值。玉米价格和单位面积产量数据均来源于农业部统计发布的《全国农产品收益资料汇编》。选取的主要省份为新疆、陕西、甘肃、宁夏、内蒙古、黑龙江、吉林、辽宁、广西、云南和重庆。
最小化问题解通过平滑参数?姿调节趋势变化,?姿为常数,需要提前给定。当?姿=0时,满足最小化问题解的趋势序列为Yt本身;当?姿→∞时,序列趋势变化接近线性时间趋势。年度数据?姿=100,季度数据?姿=1600,月度数据?姿=14400。从(4)式可以发现,当?姿=0时,趋势项序列为Yt本身;如果?姿→∞,那么整个序列就会呈现一个线性的时间趋势,故当?姿越大时,整个时间序列线性表现出越光滑的水平。
(三)边缘分布拟合
农产品产量风险和价格风险的边缘分布估计,对后文精确度量产量和价格二者之间的相关性至关重要。既往的文献研究表明,Weibull分布、Beta分布和Lognormal分布对农产品产量数据具有较好的拟合效果。Burr分布、Logistic分布和Gamma分布对农产品价格数据具有较好的拟合效果。依据既往文献研究结果选取拟合效果较好的分布类型,选取Weibull分布、Lognormal分布和Beta分布对玉米单位面积产量数据进行分布拟合;选取Burr分布、Logistic分布和Gamma分布对玉米价格序列进行分布拟合。
三、实证分析
(一)数据描述统计
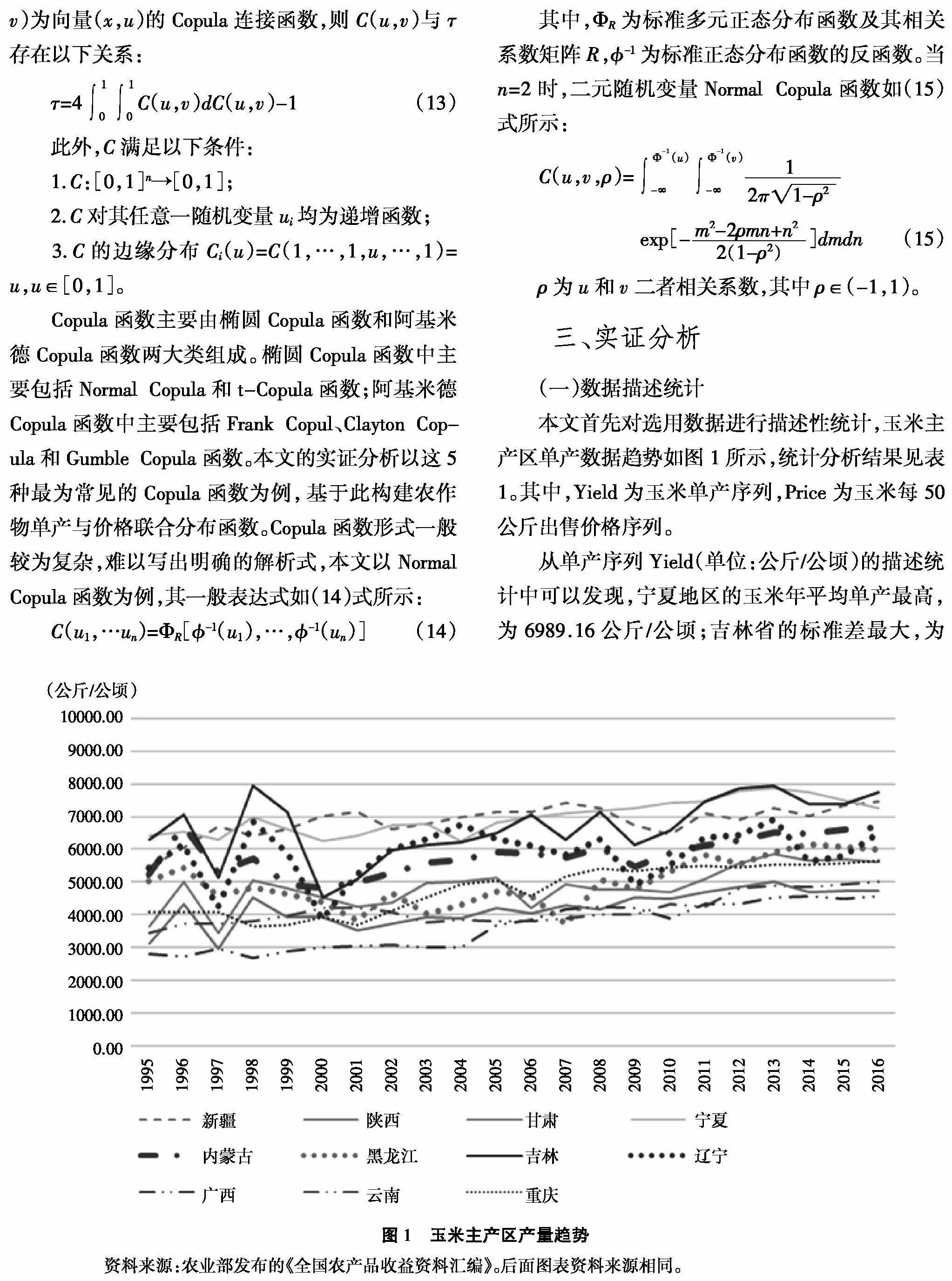
本文首先对选用数据进行描述性统计,玉米主产区单产数据趋势如图1所示,统计分析结果见表1。其中,Yield为玉米单产序列,Price为玉米每50公斤出售价格序列。
从单产序列Yield(单位:公斤/公顷)的描述统计中可以发现,宁夏地区的玉米年平均单产最高,为6989.16公斤/公顷;吉林省的标准差最大,为956.36,这说明吉林省玉米种植生产风险较高;主要省份中除了内蒙古和广西偏度值非常小,其余省份都表现出左偏或者右偏特性,新疆和辽宁玉米单产序列的偏度和峰度都较为明显,偏度分别为
-1.31和-1.04,其峰度数据都大于3,呈现出尖峰厚尾的特征。从整体看来,玉米主产区单产呈现出明显的左偏和非正态特征。
从价格序列Price的描述统计中可以发现,广西年平均玉米出售价格最高,每50公斤能卖到82.75元;辽宁省的玉米出售价格波动风险最大,标准差为27.33;主要省份中黑龙江右偏程度最高,新疆地区玉米出售价的峰度最高。从整体看来,玉米主产区单产呈现出明显的右偏和厚尾特征。
(二)边缘分布拟合结果
采用HP滤波法对所有单产数据均进行去趋势处理,剔除时间序列中的长期趋势项。选取Weibull分布、Lognormal分布和Beta分布对玉米主产区单位面积产量数据进行分布拟合,选取Burr分布、Logistic分布和Gamma分布对玉米价格序列进行分布拟合。 随后通过KS检验拟合分布优度,KS检验值越小表明拟合效果越好。主要省份玉米单产和价格序列分布拟合优度检验结果如表2所示。
从表2可以看出,主要省份中新疆、陕西、吉林、辽宁4个省份玉米单产最优分布选择为Weibull,甘肃、宁夏、内蒙古、黑龙江和云南5个省份单产序列服从Lognormal分布,仅有广西和重庆两个省份玉米单产的最优分布为Beta。价格序列中,陕西、宁夏、内蒙古和云南4个省份玉米价格序列为服从Burr为最优拟合分布,其余省份玉米价格序列的最优拟合分布为LogLogistic。
玉米单产和价格序列分布拟合如图2和图3所示(以新疆为例),图2(a)为玉米单产序列Beta分布拟合结果,Beta分布拟合表现出明显右偏特征;图2(b)为玉米单产Weibull分布拟合结果,与Beta分布拟合相比拟合效果较好;图2(c)为玉米单产Lognormal分布拟合结果,表现出尖峰特征;在图2(d)中可以清晰对比出玉米单产三种分布拟合效果,Weibull分布拟合玉米单产效果最好。图3(a)为玉米价格序列Burr分布拟合结果,图3(b)为玉米价格Logistic分布拟合结果,图3(c)为玉米价格Gamma分布拟合结果,图3(d)为玉米价格三种分布拟合对比图像。
(三)Copula函数估计结果及最优选择
在得到玉米产量和价格最优拟合分布基础上,通过Copula函数来计算产量和价格之间的相关关系。 本文选取了5种常用的Copula函数对主要省份玉米产量和价格数据联合分布进行估计,具体包括Normal Copula、t-Copula、Frank Copula、Gumbel Copula和Clayton Copula。估计方法采用两阶段极大似然估计法,估计结果如表3所示。
本文通过最小平方欧式距离法估计不同Copula函数,应用公式为:
d2=■|C(ui,vi)-■(ui,vi)|2 (16)
其中,平方欧式距离最小的Copula函数类型为最优Copula函数选择。从主要省份的多元Copula函数估计出玉米单产和价格的秩相关系数?子可以发现,新疆、黑龙江、吉林、辽宁和重庆表现出一定的正相关性,其余地区玉米单产风险和价格风险表现出一定的负相关性。单产和价格序列表现出的微弱相关性可能受选用数据长度限制的影响。从各个省份最优Copula函数选择中可以发现,服从Frank Copula函数为最优选择的地区最多,涵盖新疆、陕西、黑龙江、云南和重庆5个省份;甘肃和吉林服从t-Copula函数为最优选择;宁夏和广西两地服从Gumble Copula;辽宁服从Normal Copula;内蒙古地区服从Clayton Copula为最优函数。后文选取各个省份最优Copula函数参数为参数初始值进行数据模拟,根据产量和价格的边缘分布函数求出对应反函数值,再将生成的序列值ui和vi相乘计算出玉米的预期收入。
(四)农产品收入保险费率厘定
玉米主产区收入保险费率厘定具体步骤为:
1.根据上文中各个省份确定的最优拟合函数类型及其参数,选定最优Copula函数,利用MATLAB R2014b蒙特卡洛模拟抽样10000次, 生成[0,1]均匀分布的随机数列和。
3.根据收入保险费率公式,计算得出不同保障水平下的保费费率。
农产品收入保险期望损失值计算公式和保费计算如公式分别如(17)式和(18)式所示:
从表4中可以看出,在70%、75%、80%、85%和90%保障水平下,主要省份的玉米收入平均保费费率依次为33.0‰、38.8‰、45.3‰、52.8‰和61.7‰;
主要省份中新疆玉米收入保险费率最高,在70%、75%、80%、85%和90%保障水平下费率分别为44.1‰、53.5‰、63.2‰、73.4‰和83.7‰。另外,新疆、黑龙江、吉林和辽宁省4个省份的保费高于主要省份均值,其余省份费率均低于平均水平。这4个省份估计得出的单产和价格秩相关系数为负值, 可见产量风险和价格风险呈现一定负相关性时,在一定程度上呈现风险对冲效应。其中,吉林省玉米收入保险费率为3.33%~60.4%。周县华(2018)对吉林省玉米种植地进行风险区域划分后对种植险费率进行分级厘定,研究发现吉林省不同风险区域玉米种植险费率费率在9.23%~11.27%区间[23];付慎一(2017)基于吉林省1978—2015年玉米单产及价格指数序列, 对该地区下的各市县玉米收入保险进行费率厘定研究,测算出在85%保障水平下收入保险费率为2.45%~9.63%,发现与种植产量险相比,在同等保障水平下,收入保险费率更低[16]。本文测算结果也表明,在同等保障水平下收入保险的费率要低于种植险,在同一费率水平下,农产品收入保险提供的保障高于现行的物化成本保险。
四、结论与政策建议
(一)结论
1. 主要省份中玉米单产边缘分布拟合最优选择最多的是Lognormal分布, 仅有广西和重庆玉米单产服从Beta分布为最优选择。 价格序列中,陕西、宁夏、内蒙古和云南4个省份玉米价格序列服从Burr为最优拟合分布,其余省份玉米价格序列的最优拟合分布为LogLogistic。
2.主要省份中,多元Copula函數估计出新疆、黑龙江、吉林、辽宁和重庆5个地区玉米单产和价格序列秩相关系数为正,其余地区秩相关系数表现出一定的负相关性。Frank Copula函数是主要省份中的估计效果最好的最多选择。
3.在70%、75%、80%、85%和90%保障水平下,主要省份玉米收入保险平均费率依次为33.0‰、38.8‰、45.3‰、52.8‰和61.7‰; 主要省份中,新疆、黑龙江、吉林和辽宁省4个省份的保费高于主要省份均值,其余省份费率均低于平均水平。在同等保障水平下收入保险的费率要低于种植险,在同一费率水平下,农产品收入保险提供的保障高于现行的物化成本保险。
(二)政策建议
1.完善农产品期货市场
与发达国家农产品期货市场相比,我国农产品期货市场起步较晚,期货市场效率较低。由美国农业保险的发展史看来,期货市场具有较好的价格发现功能,还是风险分散的重要手段。农产品期货市场的发展能够为农产品收入保险定价提供大量的数据参考,农产品期货合约还能有效规避其所附带金融属性引发的价格波动风险。
我国开展农产品收入保险必须要以完善的农产品期货市场作为支撑,农产品期货市场标的物种类匮乏,直接给收入保险开展带来保险项目种类单一的阻碍。目前期货市场上主要的农产品期货合约包括早籼稻、强麦、玉米、棉花、黄大豆、豆粕和白糖等13个品种。主粮作物还能找到对应的期货合约,部分大宗商品根本无法找到对应的金融衍生品。因此,我国的农产品期货市场需要进一步深入发展与完善,不断开发新的期货期权产品的同时,完善现有期货产品交易机制。除此之外,还应组织专门的农业风险管理学习,引导农业经营主体了解多样性的风险规避手段,培养其风险防范意识。倡导农业经营主体学习应用农产品期货产品,学会通过农产品期货对冲来规避价格风险。
2.科學划分农业区域风险
风险区域的细化有助于保险公司减少保费厘定的基差风险,也有助于政府从宏观层面制定农业风险管理政策和制度。目前我国正处于农业收入保险引进阶段,农产品收入保险项目试点多为农业主产地,随着我国农业经济的发展,收入保险势必一步步延伸覆盖更多种类的农作物以及更广阔的区域。风险区域划分有利于今后保险公司因地制宜设计保单,也有助于政府因地制宜制定农业政策。
建议根据风险特征和实际情况将地域进行分类,划分为更小的风险区域单元,可以从地形地貌、自然风险、 地域属性三层维度进行风险区域细划。依据地域地理位置划分为山丘和平原两种一级风险单元,在山丘和平原风险区域单元中又根据自然灾害等级进一步分为三六九等的二级风险单元,在二级单元的基础上根据地域属性划分为三级风险单元。省级属性为第三级第一类单元,市级为第三级第二类单元,县域为第三级第三类风险单元。这种将我国地理区域精细划分的单元分割法,有助于因地制宜地设计农产品收入保险的保单条例, 也提高了保险定价的合理性,有助于农业保险高效服务于我国农业发展。
3.制定收入保险保费分级补贴与双向补贴政策
收入保险保费分级补贴政策,适用于中央向地方财政补贴农业保险保费,中央基于各区域保费差异进行保费分级补贴。各地区保费由国家农业部进行测算,在科学测算的基础上根据各地实际情况做略微调整,之后针对测算出的各地区保费水平层层分级。以本文的保费测算研究为例,实证发现主要省份中新疆、黑龙江、吉林和辽宁4个省份的保费高于主要省份均值, 故可以将其划分为高保费区,其余省份费率均低于平均水平,可以划分为低保费区;保费按照参照标准分级,参照标准可以为区域性保费均值或者其他农业险费率,中央针对主要省份农业收入保险保费补贴时,可以依据高低保费区划分进行分级补贴。建议国家农业风险管理部对我国各省农业情况进行调研,为保费区域等级划分以及保费分级补贴的调整提供参考依据。
双向补贴政策,适用于地方财政补贴投保人与农业保险公司,建议各地方政府对投保人和承保人均给予政策扶持与实际惠利。对于投保人给予保费补贴,减轻其收入保险购买成本;对于承包人给予税费优惠政策, 从需求侧和供给侧两端给予支持,刺激农业与保险业协同发展,这对农业经营体系长远健康发展具有重要意义。此外,我国各省地方财政情况不一,重点发展领域有别,应该因地制宜地制定和实施农业保险补贴政策。
参考文献:
[1]冯文丽,郭亚慧.基于Copula方法的河北省玉米收入保险费率测算[J].保险研究,2017(8):19-28.
[2]晁娜娜,杨汭华,罗少凡.基于Copula模型的棉花收入保险费率测算研究[J].统计研究,2017,34(8):92-99.
[3]BIELZ M,GARRIDO A,SUMPSI J M.Revenue Insurance as an Income Stabilization Policy:An Application to the Spanish Olive Oil sector[J].Zaragoza(Spain),2002,12(1):28-31.
[4]GHOSH S,WOODARD J D,VEDENOV D V.Efficient Estimation of Copula Mixture Model:An Application to the Rating of Crop Revenue Insurance[C].Agricultural and Applied Economics Association,2011.
[5]GRAY C L.How to Understand High Food Prices?[J].Agricultural Economics,1995,61(2):425-434.
[6]GOODWIN,B K.Modeling Crop Prices through A Burr Distribution and Analysis of Correlation between Crop Prices and Yields Using A Copula Method[J].Access & Download Statistics,2008,9(2):1-39.
[7]OSAMA A,RICHARD E.Heterogeneity and Distributional Form of Farm-Level Yields[J].American Journal of Agricultural Economics,2015,93(1):128-156.
[8]GOODWIN B K,HUNGERFORD A.Copula-Based Models of Systemic Risk in U.S.Agriculture:Implications for Crop Insurance and Reinsurance Contracts[J].American Journal of Agricultural Economics,2015,97(3):879-896.
[9]PAVLISTA M,CARL Z,MICHAEL L.Implications of within County Yield Heterogeneity for Modeling Crop Insurance Premiums[J].Agricultural Finance Review,2012,72(1):198-201.
[10]GOODWIN B K,COBLE K H,KNIGHT T O.Accounting for Short Samples and Heterogeneous Experience in Rating Crop Insurance[J].Agricultural Finance Review,2014, 73(1):139-153.
[11]GOODWIN B K.Revenue Insurance Purchase Decisions of Farmers[J].Applied Economics,2004,38(2):171-183.
[12]王克,张峭,肖宇谷,等.农产品价格指数保险的可行性[J].保险研究,2014(1):40-45.
[13]王明高,孟生旺.尖峰厚尾巨灾损失数据的组合分布模型[J].保险研究,2017(12):113-123.
[14]谢凤杰,王尔大,朱阳.基于Copula方法的作物收入保险定价研究——以安徽省阜阳市为例[J].农业技术经济,2011(4):41-49.
[15]谢凤杰,吴东立,赵思喆.基于Copula方法的大豆收入保险费率测定:理论与实证[J].农业技术经济,2017(2): 111-121.
[16]王国栋,庞楷.基于Copula函数的经济作物收入保险费率测算——以甘肃苹果为例[J].金融理论探索,2019(3):62-70.
[17]付慎一.基于多種Copula函数的农作物收入保险定价比较研究[D].长春:吉林大学,2017.
[18]庹国柱,朱俊生.论收入保险对完善农产品价格形成机制改革的重要性[J].保险研究,2016(6):3-11.
[19]钟甫宁,邢鹂.粮食单产波动的地区性差异及对策研究[J].中国农业资源与区划,2004(3):16-19.
[20]王保玲,孙健,江崇光.我国引入农业收入保险的经济效应研究[J].保险研究,2017(3):71-89.
[21]汪必旺.我国发展农产品收入保险的效果模拟研究[D].北京:中国农业科学院,2018.
[22]刘素春,刘亚文.农产品收入保险及其定价研究——以山东省苹果为例[J].中国软科学,2018(9):185-192.
[23]徐婷婷,孙蓉,崔微微.经济作物收入保险及其定价研究——以陕西苹果为例[J].保险研究,2017(11):33-43.
[24]周县华.我国种植业保险风险区划与分级费率定价研究——以吉林省玉米种植保险为例[J].保险研究,2018(2):72-84.
