移动机器人滑模路径的跟踪控制*

宁洪斌，祝俊伟，邓小飞，陈善荣，何 亮

(1.吉首大学信息科学与工程学院，湖南 吉首 416000；2.中国联合网络通信有限公司邵阳市分公司，湖南 邵阳 422000；3.国家电网湖南省电力有限公司湘西经济技术研究所，湖南 吉首 416000)

机器人诞生是20世纪科学技术的一大进步.近些年，机器人技术不断向智能化、多元化方向发展.移动机器人集成了传感器技术、机械技术和计算机技术，是机器人研究中的一个重要分支[1-2].由于移动机器人是一种高度复杂的非线性系统，导致获得高精度的移动机器跟踪结果十分困难，因此路径跟踪精度问题被广泛关注[3-9].21世纪以来，移动机器人已被广泛应用于各个领域，并仍具有广阔的研究和应用前景.为了增强移动机器人滑模路径跟踪控制的抗干扰能力，提升控制器的动态性能及路径跟踪精度，在前人研究成果的基础之上，笔者提出了一种基于有界输入的滑模路径跟踪算法.改进的滑模控制器具有更高的跟踪精度和更好的跟踪效果，且保证了移动机器人的全局渐近稳定路径跟踪控制.

1 移动机器人的模型

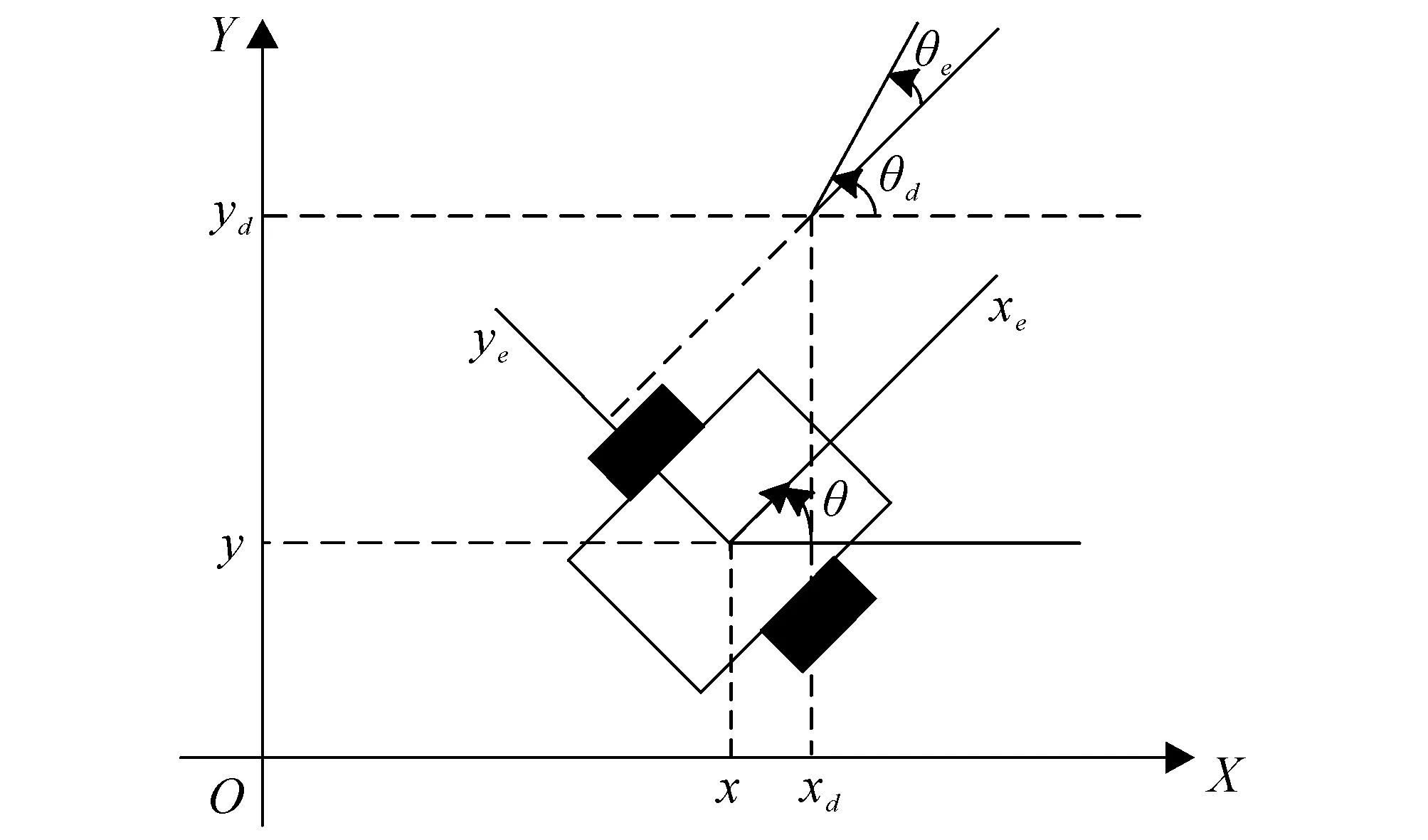
图1 移动机器人位姿误差示意Fig.1 Schematic Diagram of Pose Error of Mobile Robot

独立双后轮差动驱动移动机器人通过2个后轮的不同速度来控制机器人的速度和方向.在移动机器人的工作平面内建立直角坐标，其位姿误差如图1所示.

根据图1所示模型，得到机器人的运动学模型方程和目标轨迹方程分别为

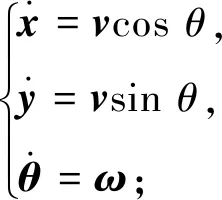
(1)

(2)

然后由坐标基本变换公式，并结合图1得到移动机器人的位姿误差方程

(3)

2 基于反演设计的滑模路径跟踪控制

反演设计方法的基本思想是，将复杂的非线性系统分解成不超过系统阶数的子系统，然后为每个子系统分别设计Lyapunov函数和中间虚拟控制量，一直后退到整个系统，直至完成整个控制律的设计.假设被控对象为

则其基本的反演设计方法步骤如下：

(ⅰ)定义位姿误差e1=x1-xd.

垦利油田群位于渤海南部海域，经多年开发，周边已建立多座平台和相应的海底管线。新油田在开发研究过程中需对周边各种依托可能性进行研究，即该稠油与周边各油田油品掺混后外输至FPSO或陆上终端储存。这就需要对各种方案开展实验，研究掺混不同油品的黏温特性。若一一开始实验，会严重影响油田的开发进程，造成不必要的人力和财力浪费。其可行的方法是研究该油田原油掺混黏度相关规律，通过计算预测掺混后黏度数据，用于依托海管的计算。

所以

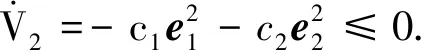
通过设计控制律，使得系统满足Lyapunov稳定性理论条件[10]，e1和e2以指数形式渐近稳定，从而保证系统具有全局意义下指数的渐近稳定性.

反演控制器的设计步骤如下：

(8)

(ⅱ)取切换面函数s1=e1，s2=e2.通过设计虚拟控制量β，使得

(9)

β=arctan(|m1|/|m2|),v=u2/sinβ.

(ⅴ)取切换面函数s3=e3，将角速度控制律设计为

(4)

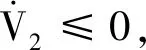
为了消除干扰，采用低通滤波器Q(s)，

(5)

3 基于有界输入的改进型滑模路径跟踪控制

设需跟踪的路径为φ*(·)=(x*(·),y*(·),θ*(·)).若机器人能够收敛并遵循约束条件，则可跟踪路径.此时定义|v*(t)|，|ω*(t)|的范围如下：

其中v*(t)和ω*(t)分别为控制输入线速度和角速度与时间相关的函数.

根据移动机器人的模型(1)，如果φ*(·)=(x*(·),y*(·),θ*(·))可跟踪，那么移动机器人的输入也必须满足约束条件(4).也就是说，对于∀t≥0，都有

(6)

条件(5)和(6)确保机器人在约束输入下跟踪φ*(·)，因此它们是φ*(·)作为可跟踪轨迹的必要条件.接下来定义

(7)

由于可实现e1,e2→0，因此实现tanh(pe1),tanh(qe2)→0，此时可将(7)式中的减数分别用m1，m2来替代，并通过设计虚拟控制量β，使得

(8)

将(8) 式变形，则虚拟控制律和线速度分别设计为

角速度控制律(4)不变，并采用低通滤波器(5)消除干扰.

在构建控制器之后还需要判断该控制器是否满足系统的稳定性，如果设计不合理，系统在控制过程中就会产生不稳定现象，系统误差会越来越大，从而导致试验失败；因此，稳定性分析是十分有必要的.

(9)

设计切换函数，使得s1,s2→0.选取等速趋近律，令

(10)

4 仿真分析

图2 正弦曲线跟踪效果对比Fig.2 Tracking Effect Comparison of Sine Curve

对改进后的移动机器人路径跟踪进行Matlab仿真，初始位姿为(0.4，-0.2，0)，期望轨迹为|xd|=t，|yd|=sin (0.5|xd|).采用基于反演设计的滑模控制器跟踪正弦曲线路径时，取k1=k2=0.3，k3=0.5，q=3；采用基于有界输入的改进滑模控制器跟踪正弦曲线路径时，取a=b=1.0，p=q=10.

图2示出2种不同方法下的跟踪效果对比.由图2可见，基于有界输入的改进控制器在0.2 s内就实现了精确的路径跟踪，而基于反演设计的滑模控制器在6.3 s后才实现较准确的路径跟踪.这说明基于有界输入改进法明显比基于反演设计法的动态性能好.

图3示出x和y方向的跟踪效果对比.由图3可见：在x方向上，2种方法的跟踪效果区别不大，但基于有界输入改进法仍然比基于反演设计法的效果要好；在y方向上，基于有界输入改进法明显比基于反演设计法的动态响应快.

图4示出控制输入的线速度和角速度曲线.由图4可见，2种方法的控制都较平稳，相对来说，基于有界输入改进法的控制输入更理想.

图3 x和y方向跟踪效果对比Fig.3 Tracking Effect Comparison of x and y Direction

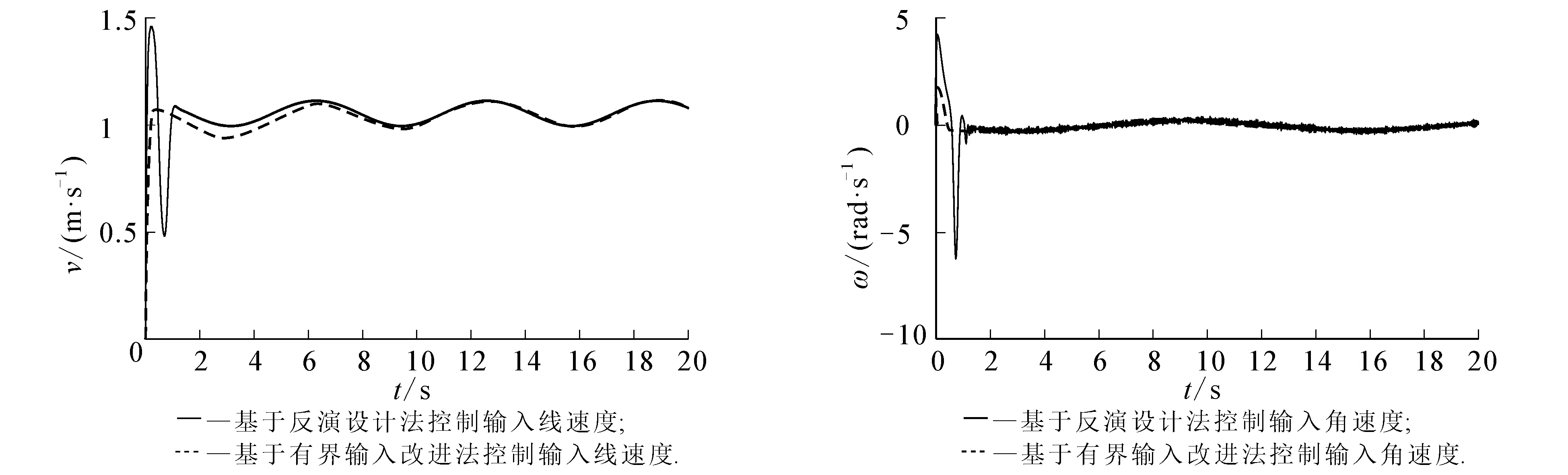
图4 控制输入的线速度与角速度曲线Fig.4 Linear Velocity and Angular Velocity Curves of Control Input

5 结语

利用反演设计的思想设计了滑模控制器，并采用低通滤波器有效地减弱了干扰，提高了系统的鲁棒性.由于控制器的动态性能不理想，因此在此基础上做了相应改进，即给出了有界输入须满足的约束条件.实验结果表明，在相同的参数条件下，基于有界输入的滑模控制器在0.2 s内就实现了精确的路径跟踪，而基于反演设计的滑模控制器在6.3 s才实现较精确的路径跟踪.笔者验证了基于有界输入改进控制器的可行性和有效性，为更准确、更快速地实现移动机器人跟踪控制奠定了基础.