分数阶不确定超混沌Bao系统滑模同步的两种方法

李巧利, 毛北行

(1.河南工业大学 理学院，河南 郑州 450001;2.郑州航空工业管理学院 理学院,河南 郑州 450015)

对分数阶系统的混沌同步及滑模同步的研究，众多学者已有丰富的成果[1-7].文献[8]研究分数阶多涡卷混沌系统的自适应滑模同步控制问题，文献[9]利用积分滑模方法研究分数阶Victor-Carmen混沌系统同步问题，文献[10]根据积分滑模控制方法研究航天器的姿态容错控制，文献[11]根据比例积分滑模控制研究滑模制导律问题，文献[12]根据比例积分滑模方法研究纠缠混沌系统的同步问题.另一方面,Bao混沌系统激起了广大学者的研究兴趣.文献[13]研究一类4维Like-Bao系统的动力学分析问题，文献[14]研究分数阶超混沌Bao混沌系统的比例积分滑模同步，文献[15]研究超混沌Bao系统线性状态反馈控制及自适应控制.论文研究不确定分数阶超混沌Bao系统滑模同步的两种方法．

1 主要结果

定义1[16]Caputo分数阶导数定义为

分数阶超混沌Bao系统[14]为

(1)

当a=20,b=4,c=32,d=4,q=0.95时，系统的Lyapunov指数分别为1.987，0.071，0.000，-18.058.系统的超混沌吸引子如图1所示.

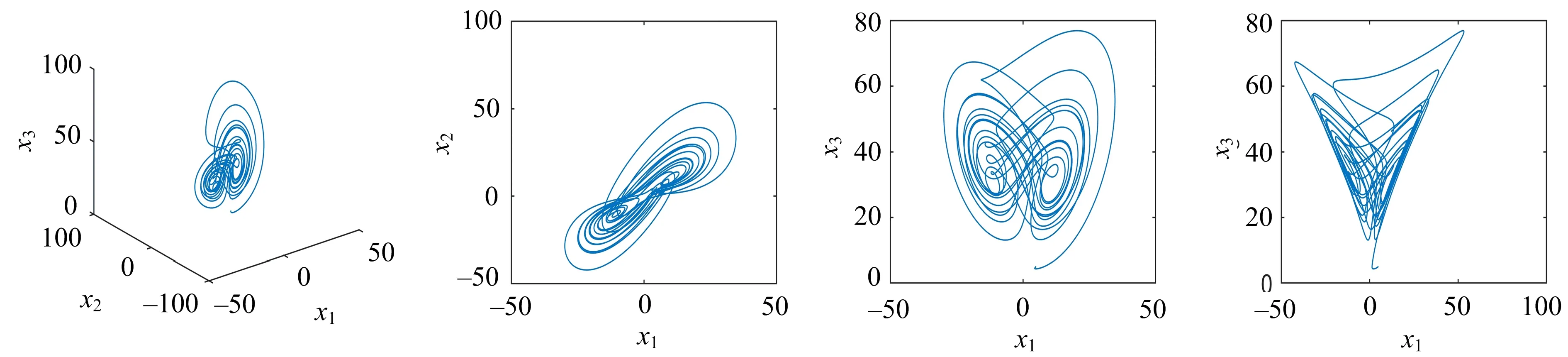
图1 系统的混沌吸引子

设计从系统为

(2)

其中：Δfi(y)为不确定项，y=[y1,y2,y3,y4]T，di(t)为系统外扰，ui为控制.

定义误差e1=y1-x1,e2=y2-x2,e3=y3-x3,e4=y4-x4，得误差方程为

(3)

假设1|Δfi(y)|≤mi,|di(t)|≤ni,mi,ni>0.

假设2|Δfi(y)+di(t)|<λ|ei|,其中，λ为大于零的常数．

引理1[16]若x(t)为连续可微的函数，则有

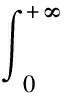
定理1若满足假设1，2，构造滑模函数为

控制器为

则(2)，(3)是滑模同步的．

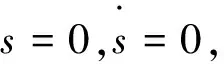
代入控制器，(3)的第一个方程可写为

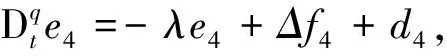
所以e4→0.

两边积分，有

根据引理2，得到s(t)→0.

假设3|ae1-ae2+Δf1(y)+d1(t)|<λ|e1|.

假设4|y1y3-x1x3-ce2+e4+Δf2(y)+d2(t)|<λ|e2|.

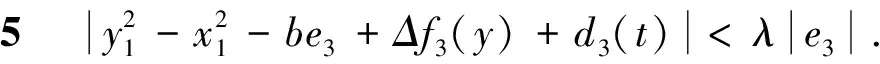
假设6|de1+de2+Δf4(y)+d4(t)|<λ|e4|.

定理2若满足假设3～6，设计滑模函数为

控制器为

其中:λ>0为常数，则(2)，(3)是比例积分滑模同步的．

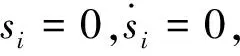
(4)

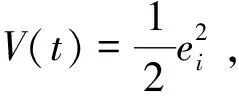
两边积分，有

根据引理2， 得到s(t)→0.

2 Matlab仿真

选取系统参数a=20,b=4,c=32,d=4,q=0.95,初始值设置为(x1(0),x2(0),x3(0),x4(0))=(2.2,6.5,2.5,2.5).

Δf1(y)+d1(t)=0.1sin(t)y1+0.1cost,Δf2(y)+d2(t)=-0.1cos(t)y2+0.1cost,

Δf3(y)+d3(t)=-0.1sin(t)y3+0.1cos(2t),Δf4(y)+d4(t)=0.1cos(t)y4+0.1sint.

系统误差曲线如图2,3所示.从图中可以看出，初始时刻系统误差较大，随着时间推移系统误差曲线趋向一致．定理2构造了4个分数阶比例积分滑模面，控制器变得更加简单，较定理1更加易于实现．

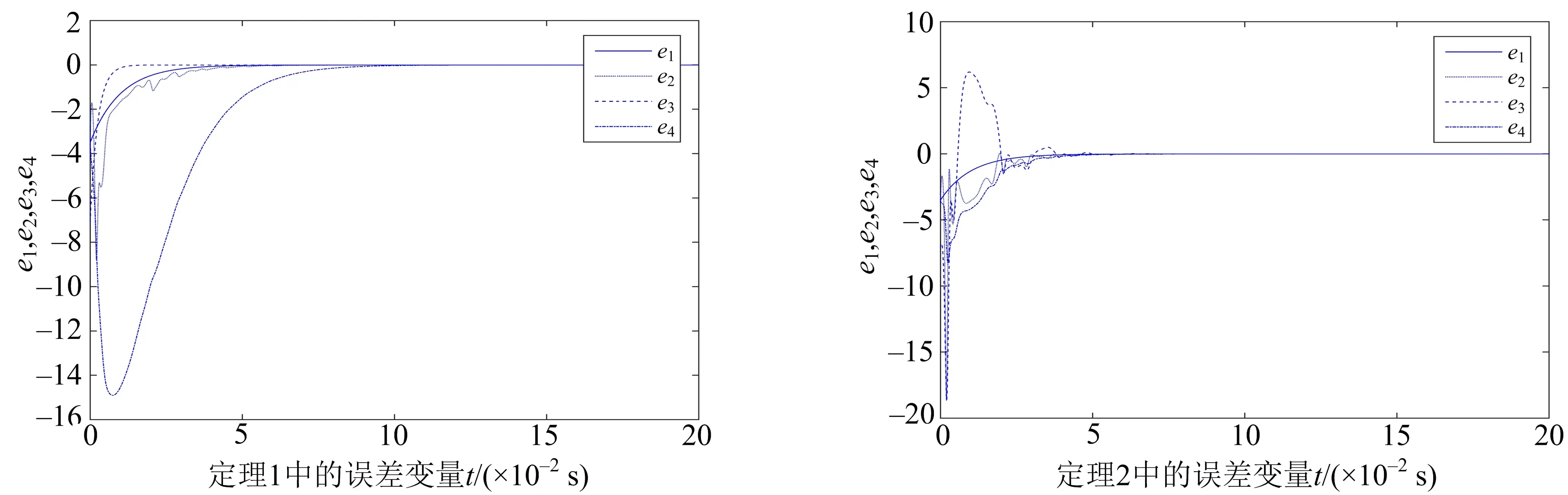
图2 定理1的系统误差曲线 图3 定理2的系统误差曲线

3 结束语

研究分数阶不确定超混沌Bao系统的滑模同步，得到分数阶不确定超混沌Bao系统取得滑模同步的两个充分条件，从数学角度给出了严格的证明和逻辑推理过程，用Matlab数值算例验证了方法的正确性．