基于变化的水热耦合平衡方程参数预测区域水资源量
2020-03-20石清邢万秋
石清, 邢万秋
(1.中冶华天南京工程技术有限公司,江苏 南京 210019; 2.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098; 3.河海大学 水文水资源学院,江苏 南京 210098)
近几十年来,众多研究沿着气候变化的方向对水文循环过程和水资源进行模拟和预测[1-5]。其中广泛应用于气候变化背景下径流响应预测的方法主要有两类:基于水文模型的方法和基于Budyko假设的水量平衡方法[6]。在年以上的尺度,基于Budyko假设的水量平衡方法以水量平衡为基础,在减少不确定性方面具有优势,可用于预测评估未来径流的变化,而目前通过Budyko水热耦合平衡方程的方法对区域水资源进行预测的研究较少。水文模型在预测未来水资源量时均基于历史时期率定和验证后的模型参数,同样地,基于Budyko水热耦合平衡方程在对未来区域水资源量进行预测时,以往的研究多假设Budyko方程中的参数在未来气候情景下恒定不变。实际上,随着未来气候情景的变化、流域特征的改变和人类活动的加剧,区域水热耦合平衡状态也将随之发生改变。在气候条件和水文情势发生改变的同时,Budyko方程参数应是变化的。因此,综合考虑气候变化和Budyko方程参数的变化进行区域水资源量预测极有必要。
为此,本研究选取了代表我国不同气候区的3个典型流域(松花江流域、黄河流域和珠江流域),通过研究其水文气象变量的变化趋势,计算分析Budyko参数的变化规律,利用基于Budyko方程的动态水量平衡模型实现3个流域未来的水资源量预测。
1 研究区概况
选取分别代表我国不同气候区的珠江流域(河源站控制的东江流域)、松花江流域(丰满水库站控制的松花江上游流域)和黄河源区(唐乃亥水文站控制流域)作为典型流域,如图1所示。
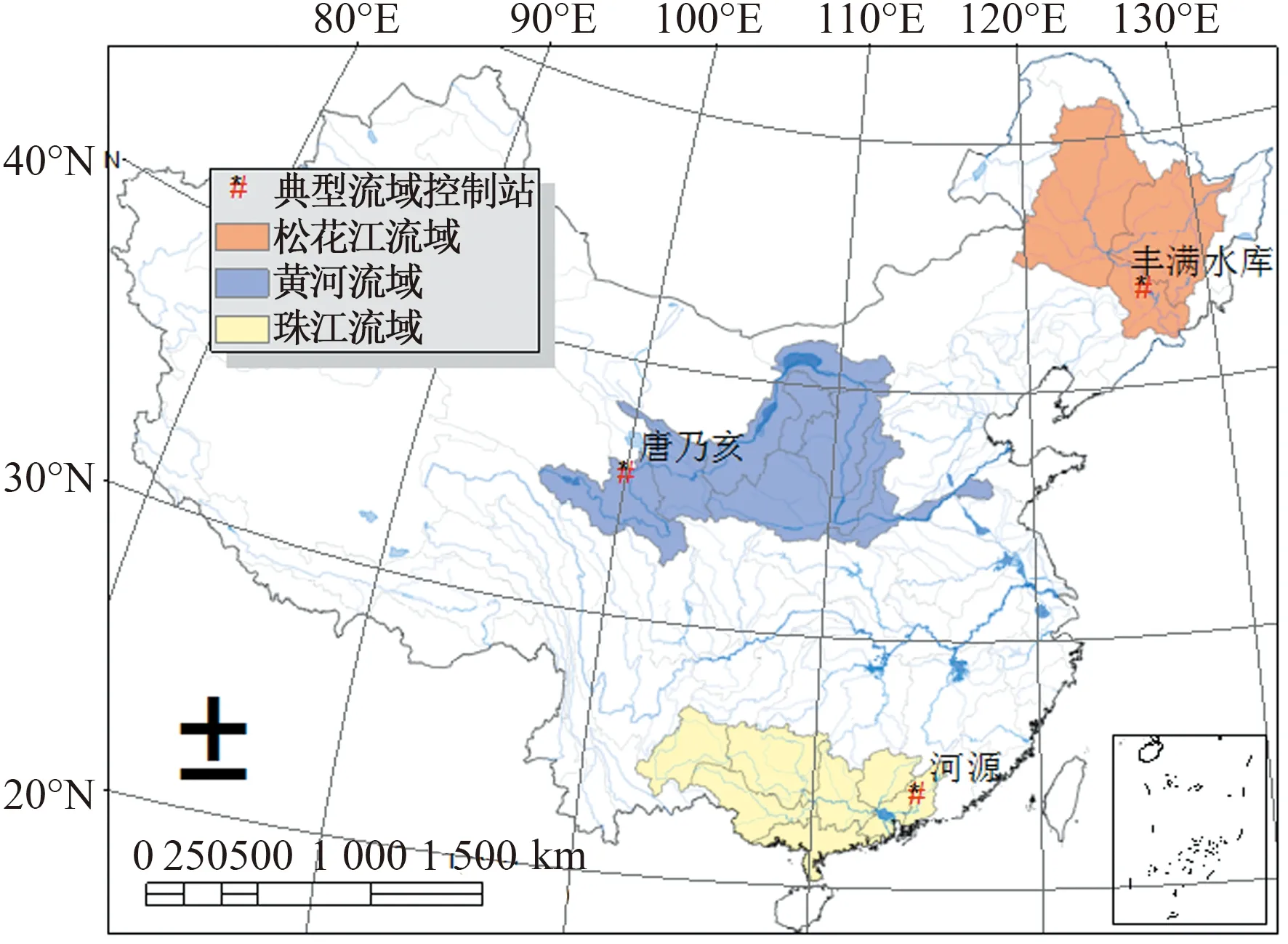
图1 研究选取的典型流域
河源水文站位于广东省河源市,控制东江秋香江口以上区域,流域面积为15 750 km2;东江流域属亚热带季风气候,四季不甚分明,年平均气温为22.1 ℃,多年平均降水量约为2 000 mm。丰满水库水文站位于吉林省东部山地的西侧,地处松花江上游,控制面积42 500 km2;松花江流域地处北温带季风气候区,大陆性气候特点显著,多年平均气温为3~5 ℃,年内温差较大,多年平均降水量约为700 mm。黄河源区地处青藏高原东部边缘,以唐乃亥水文站断面为界,流域面积121 972 km2;属高原山地气候,海拔较高,多年平均气温仅为1 ℃,多年平均降水量约350 mm。
2 数据处理与研究方法
2.1 气候情景数据
本研究采用CMIP5公开的4种气候模式(包括BCCCSM1-1M、GFDL-ESM2M、HadGEM2-ES以及MIROC-ESMCHEM,发布机构和模式的空间分辨率见表1),气候情景采用3种不同的辐射强迫和大气排放标准,即低排放情景(RCP2.6)、中间稳定排放情景(RCP4.5)和高排放情景(RCP8.5)。未来情景数据选用降水量、最高气温和最低气温、潜在蒸发量4个变量。

表1 选用的气候模式发布机构及其分辨率
2.2 研究方法
2.2.1 基于Budyko方程的动态水量平衡模型
Budyko方程描述了实际蒸发依赖于潜在蒸发量(热能来源)和可利用水量(水量来源)的程度,利用Budyko框架可以有效评价气候、植被和水文循环之间的相互影响。其中,经量纲分析和数学推导并被广泛应用的傅抱璞公式[7]可以较好地表达流域内的水热耦合状态。YANG H等[8]以傅抱璞公式为基础,将Choudhury公式变换成另一种表达Budyko曲线的方程,如下:
(1)
式中:E为实际蒸发量,mm;E0为潜在蒸发量,mm;P为降水量,mm;n为参数,需要率定。
在计算潜在蒸发量E0时,由于具有物理机理的Penman-Monteith方法对资料要求较高,容易造成该方法与其它简化经验公式(如Hargreaves方法)同样甚至更差的水文循环模拟效果[9]。为此,本文选择改进的Hargreaves公式,仅需降水量、最高气温、最低气温等数据输入,具体公式如下:
E0=0.001 3S0(Tmean+17)(TD-0.012 3P)0.76。
(2)
式中:Tmean为某天中最高与最低气温均值;TD为最高与最低气温差值;S0为太阳能辐射的水当量,与测站所在的地理纬度有关[10]。
依据流域水量平衡原理,可建立动态的水量平衡模型:

(3)
式中:Sc(t)为流域总蓄水量;P(t)、E(Sc,t)和R(Sc,t)分别为流域的降水量、蒸发量和径流量。多年平均稳定状态下,Sc(t)=0[11]。
2.2.2 气候模式数据处理方法
1)偏差修正法。在用气候模式数据对区域气候水文预测时,由于气候模式数据分辨率较低以及区域的不匹配性,首先要对气候模式数据进行降尺度和偏差修正。将气候模式较粗的网格数据降尺度到0.5°×0.5°网格上,然后再求流域平均值。偏差修正法公式如下:
(4)

2)气候模式数据有效性评价法。为了较系统地评价气候模式数据与实测数据的模拟效果,采用确定性系数R、效率系数Ens来分别衡量模型对量及变化趋势的捕捉能力,利用平均变差BIAS来评价模型的系统偏差,用标准偏差的比值RS来检验模型对指标变率的捕捉能力。各计算公式如下:
(5)
(6)
(7)
(8)

除上述方法之外,本研究还采用了时间序列趋势检验法对降水、径流、气温等水文气象要素以及Budyko参数的变化规律加以分析;采用了滑动平均法结合最小二乘法推求Budyko方程参数。
3 结果分析
3.1 水文气象变量变化趋势
对历史时期1956—2000 年间的降水量、潜在蒸发量、最高和最低气温4个水文气象变量的趋势变化加以分析,结果如图2所示。图2中,P为降水量,E0为潜在蒸发量,Tmax为最高气温,Tmin为最低气温。1956—2000年水文气象变量变化及其显著性结果见表2。表2中坡度和p分别为线性回归的坡度值和显著性;Z为Mann-Kendall显著性检测值;“*”、“**”和“***”分别代表显著性检测通过90%、95%和99%置信水平。
由图2可见:黄河流域的降水量、最高气温、最低气温和潜在蒸发量均呈增加或升高趋势,其中,最高气温和最低气温上升趋势显著(见表2);松花江流域上的降水量呈现非显著性的降低趋势,气温显著增加,潜在蒸发量非显著上升;珠江流域上的降水量呈增加趋势,最低气温呈显著上升趋势,而最高气温和潜在蒸发量却呈下降趋势,其中潜在蒸发量下降趋势显著(通过T参数检验90%置信区间)。
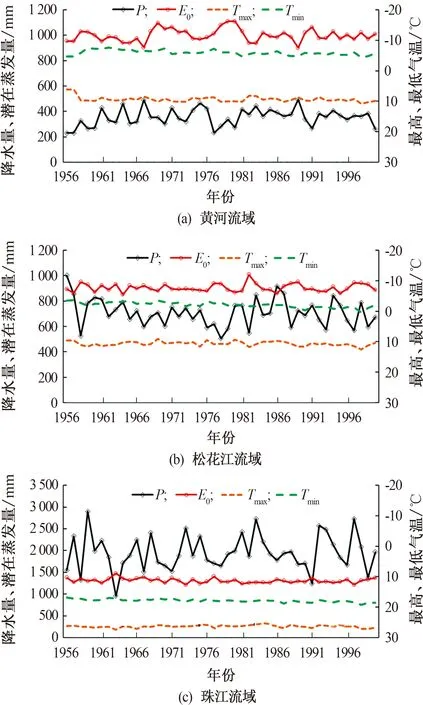
图2 1956—2000年水文气象变量变化过程
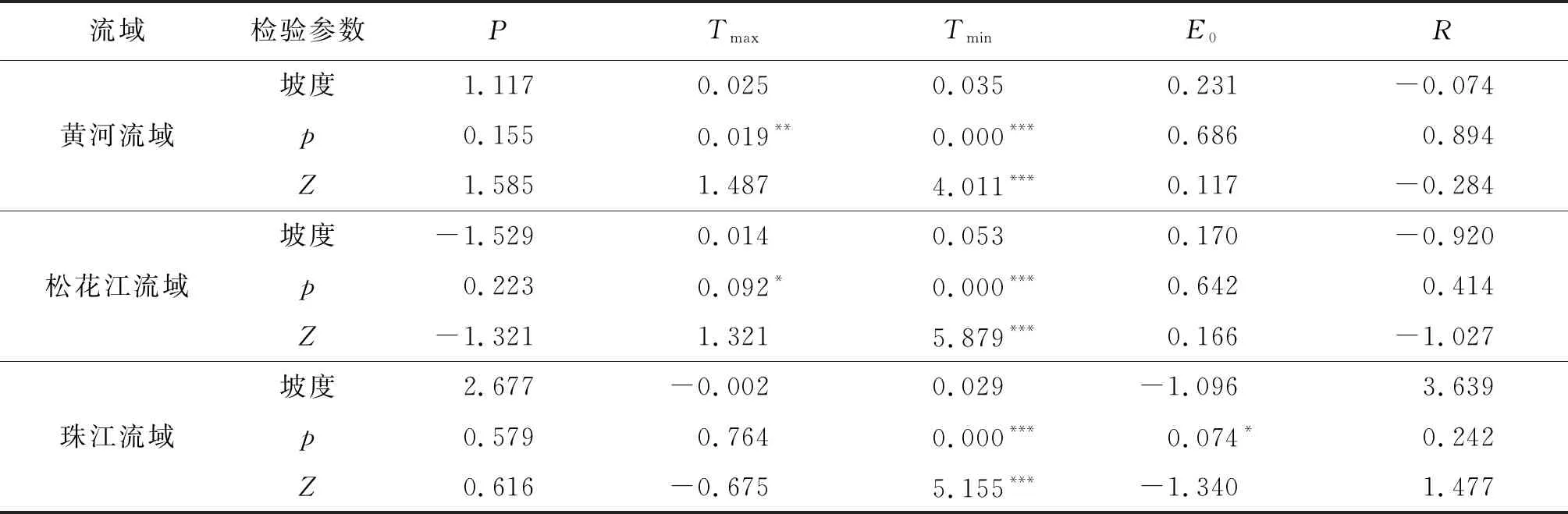
表2 1956—2000年水文气象变量变化及其显著性
3.2 Budyko方程参数的变化
对实测1956—2000 年降水量、潜在蒸发量和径流深用11 a窗口移动对其进行平滑和滤波处理,再通过最小二乘法求得每个滑动窗口的Budyko方程参数,Budyko方程参数变化趋势及其显著性结果见表3,参数结果如图3所示。
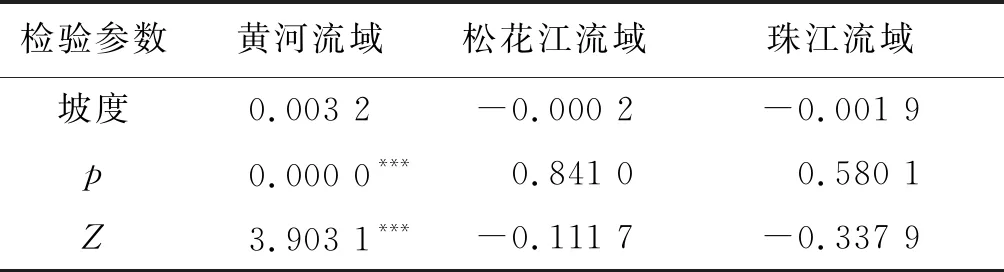
表3 Budyko方程参数变化趋势及其显著性
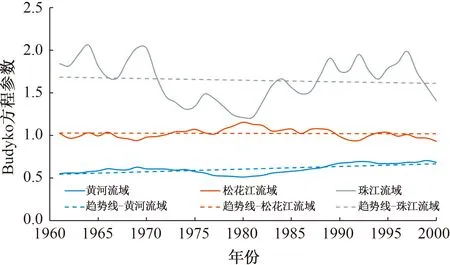
图3 11 a滑动平均后Budyko方程参数变化
由图3和表3可看出:除了黄河源参数滑动平均值序列呈显著增加趋势(通过0.01 显著性检验)外,其他两个流域(松花江流域和珠江流域)上的Budyko 方程参数均呈非显著性的减小趋势;珠江流域上参数的滑动平均值序列在历史时期变化幅度较大,而黄河流域和松花江流域上的参数值序列变化较为平稳。
3.3 区域水资源量预测
3.3.1 气候模式数据处理结果
根据历史实测降水量、最高气温、最低气温计算潜在蒸发量E0,作为历史实测E0的标准值。气候模式数据经降尺度和偏差修正后,历史时期的气候模式数据和历史实测月值序列相比较,结果见表4(以黄河流域为例)。表4中:4个变量中最高气温的模拟效果最好,最低气温的次之,降水量的模拟效果最差;4个气候模式中,以GFDL模式对黄河流域上的水文气候变量模拟精度最高,以HadGEM2模式对黄河流域上的水文气候变量的模拟精度最低;4种气候模式均在一定程度上较好地模拟了区域水文气候变量,本文采纳4种气候模式数据进行研究。
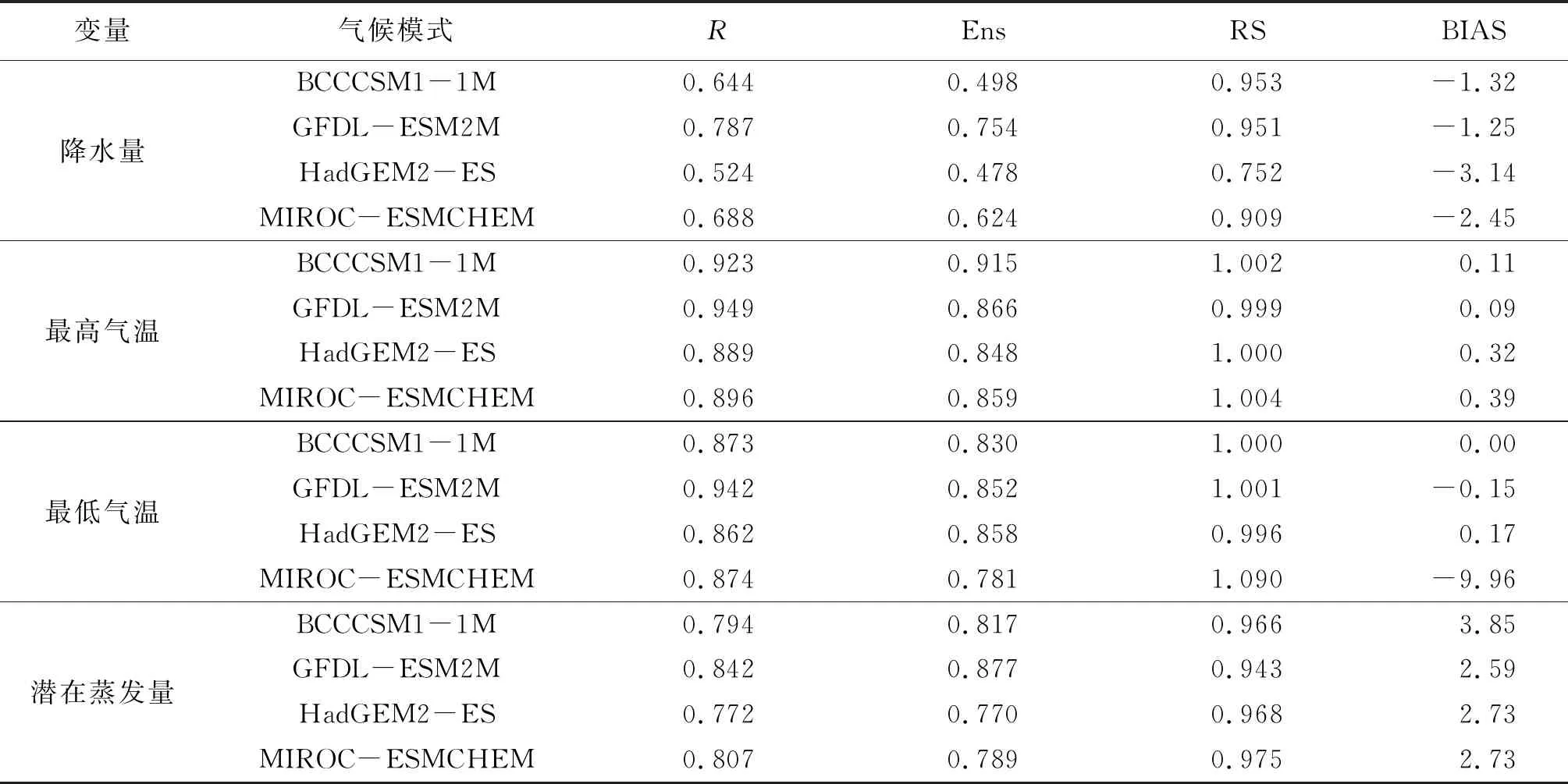
表4 历史的气候模式数据和历史实测月值数据的比较
图4给出了黄河流域上历史实测数据和气候模式RCP2.6情景下数据的11 a滑动平均值长期序列。
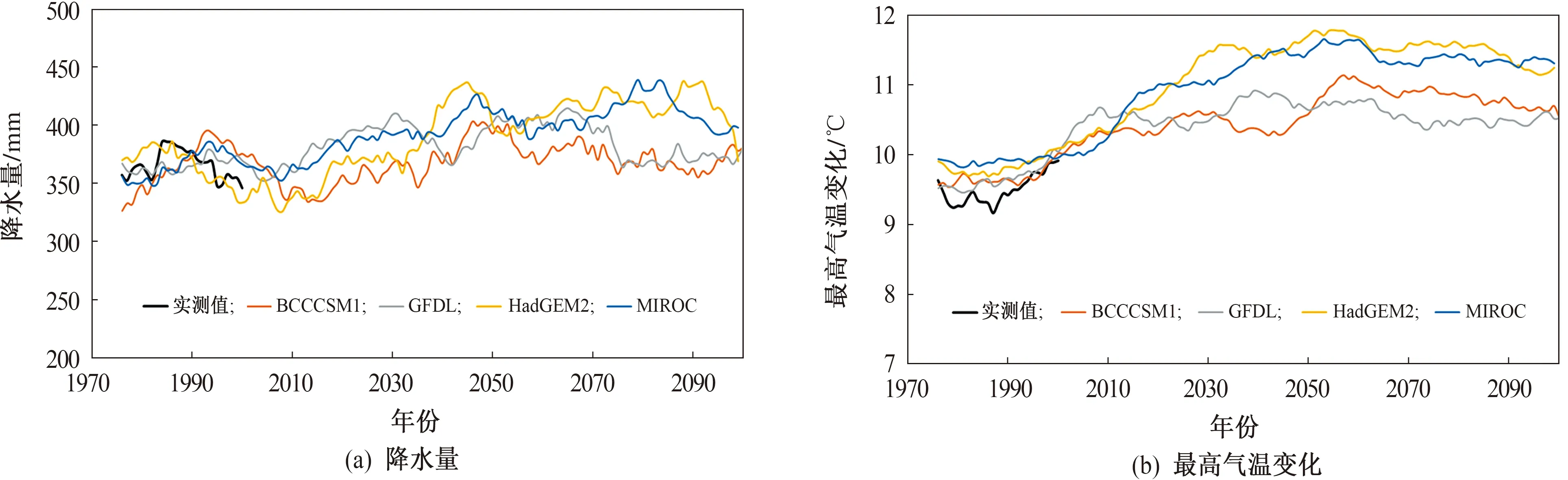
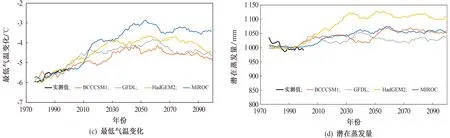
图4 气候模式数据和实测历史数据长期序列11 a滑动平均值
由图4可见,历史时期4种气候模式对潜在蒸发量的模拟结果较为一致,同时未来情景下潜在蒸发量呈现增加的趋势。
3.3.2 2021—2050年多年平均径流预测结果
采用4种气候模式、3种气候情景,基于黄河流域、松花江流域和珠江流域重新构建的区域Budyko水热耦合平衡方程,计算未来时段(2021—2050年)区域水资源量。3个流域的降水量、潜在蒸发量、最高气温和最低气温的变化如图5所示。图5中,在3个典型流域,最高气温和最低气温均随着辐射强迫和大气排放标准的升高而变幅增大。
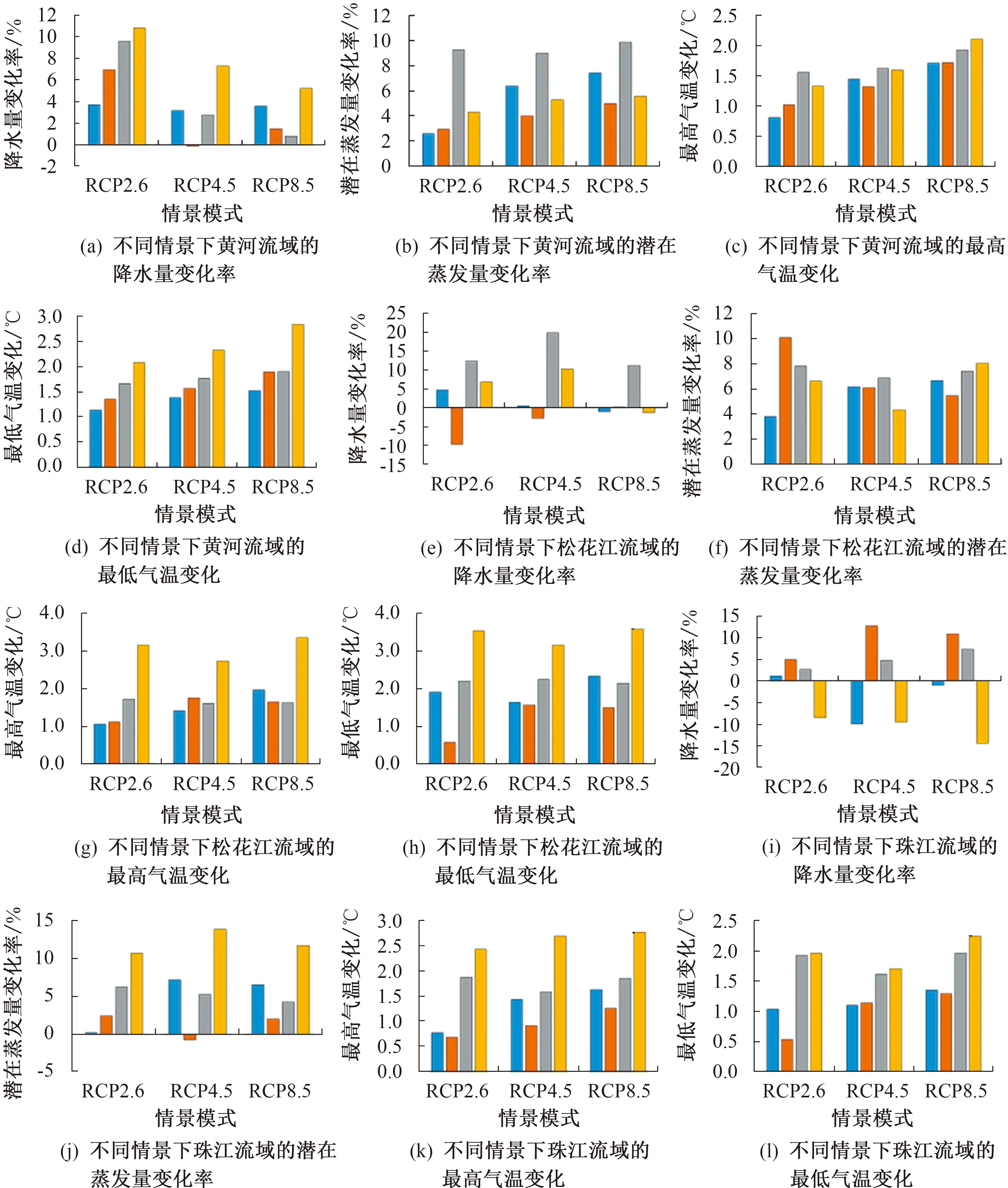
图5 未来时段(2021—2050年)降水量、潜在蒸发量、最高气温、最低气温相对基准期(1971—2000年)的变化率或变化
从图5中可以看出:相较于各气候模式的历史时期均值,黄河流域在未来时段(2021—2050年)内4个水文气象变量均增加,同时MIROC模式的降水量、最高气温和最低气温在4个模式中增幅最大,而潜在蒸发量在HadGEM2模式下的变化率最大;潜在蒸发量、最高气温和最低气温随着辐射强迫和大气排放标准的升高而变化率或变幅增大,而降水量则相反;松花江流域2021—2050年内降水量在GFDL模式下相较于历史时期将减少,潜在蒸发量在GFDL模式下随着排放情景的升高而变化率变小,在BCCCSM1模式下随着排放情景的升高而变化率增大;珠江流域在MIROC模式下的降水量随着排放情景的升高而减小幅度变大,而在HadGEM2模式下刚好相反;相较于黄河流域和松花江流域,珠江流域除MIROC模式外,潜在蒸发量在未来时段(2021—2050年)的变化率较小。
图6显示出未来时段(2021—2050年)3个典型流域上Budyko水热耦合平衡方程参数与历史1971—2000年同时期参数的对比。
由图6可以看出,黄河流域的水热耦合平衡方程参数自1971—2000年间的0.609增加到2021—2050年间的0.771,松花江流域和珠江流域的参数分别从1.032、1.560减小到0.921、1.494。说明未来时段(2021—2050年)相较于历史时期,黄河流域下垫面改变将变大,流域特征对流域水循环过程的影响将加剧;而松花江流域和珠江流域的下垫面改变将减弱,对流域水循环过程的影响将减弱。

图6 2021—2050年与历史1971—2000年的Budyko方程参数变化
图7给出了未来时段(2021—2050年)内3个典型流域的模拟径流深相较于历史实测径流深的变化。
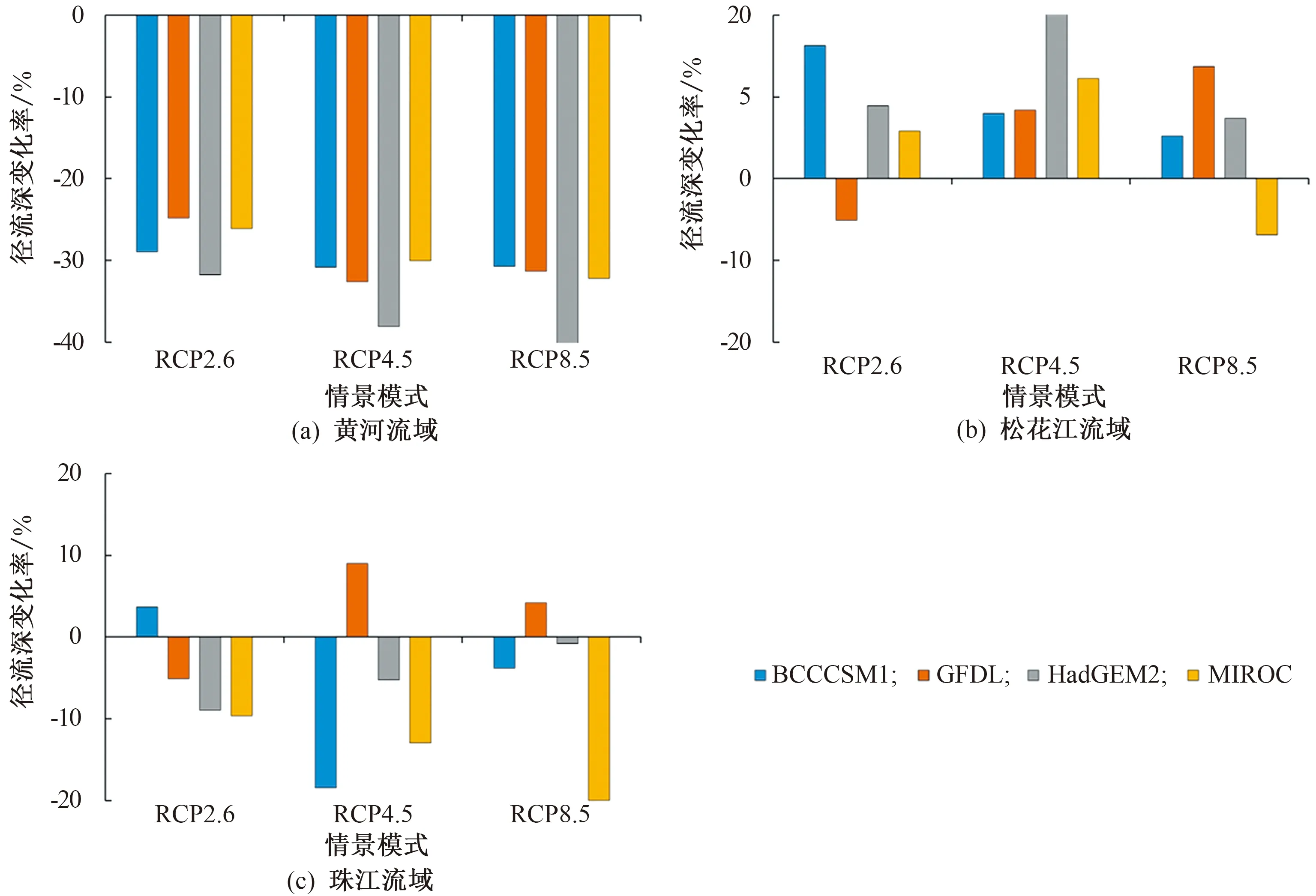
图7 气候模式下2021—2050年相较于1971—2000年实测平均径流深的变化率
由图7可以看出:黄河流域未来时段(2021—2050年)的径流均值相较于基准期的均将减少,3种气候排放情景下径流的变化率差别不大,在HadGEM2模式下径流减少的百分率最大,在RCP 8.5情景下达到40%;松花江流域在2021—2050年的径流深多年平均值相较于基准期基本均将增加,仅RCP2.6情景下的GFDL模式、RCP8.5情景下的MIROC模式预测的径流深减少,减少率均在10%以内;珠江流域在2021—2050年预测径流深将减少,仅RCP2.6情景下的BCCCSM1模式、RCP4.5和RCP8.5情景下的GFDL模式的径流深将增加。
综合图5—7得到以下结论:预测的黄河流域未来时段(2021—2050年)降水量增加而径流深却将减少,可能是由于Budyko方程参数变大导致;松花江流域未来时段(2021—2050年)的降水量增加、潜在蒸发量增加、Budyko方程参数减小,未来径流深也将增加;珠江流域未来时段(2021—2050年)的降水量减小,未来径流深也将减少。
3.3.3 与恒定Budyko方程参数预测结果的比较
为评价Budyko方程参数对区域未来水资源量的影响,假设未来气候情景下Budyko方程参数维持在基准期1971—2000年的恒定不变,以此参数预测2021—2050年的多年平均径流深,用变化的Budyko方程参数预测未来径流深的变化率,结果见表5。

表5 基于基准期Budyko方程参数预估2021—2050年的径流深变化率 %
从表5中可以看出:仅气候发生改变而流域下垫面不变的情况下,4种气候模式预测的3个典型流域上的径流深在未来30 a的均值大多将减少,和基准期实测径流深相比,BCCCSM1气候模式下以珠江流域上RCP4.5情景下减少量最大,为-18.6%,该期间降水量的变化率为-9.9%;GFDL模式下预测的2021—2050多年平均径流深相较于其他气候模式的变化率最小,在松花江流域和珠江流域的中高排放情景下(RCP4.5和RCP8.5)的径流深微弱增加;HadGEM2模式下预测的3个流域上的径流深均将减少,仅在松花江流域RCP4.5情景下的径流深增加10.9%(预测的降水量将增加19.9%);MIROC模式下预测的径流深也都将减少,仅松花江流域上RCP4.5情景下的径流深将增加2.5%。
结合图7和表5可知:尽管未来气候情景下预测的黄河流域径流深在未来期间(2021—2050年)都减少,但相比基于变化的Budyko方程参数预测的径流深减少得更多。
实际上在预测区域未来(2021—2050年)水资源量时,仅考虑气候情景的变化是不够的,本文基于前面的研究对代表流域下垫面的Budyko方程参数进行了预测,基于气候变化和流域下垫面改变预测的未来(2021—2050年)径流的变化将更准确;以RCP4.5 情景为例,图8给出了Budyko 方程参数变化前、后预测的径流变化率的对比。
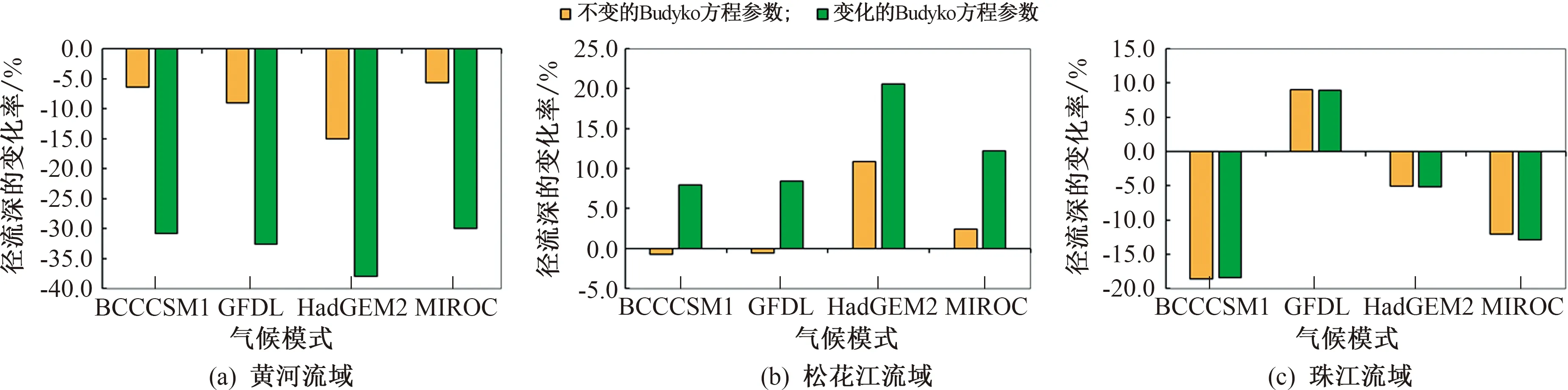
图8 RCP4.5 情景下Budyko方程参数变化前后预估径流变化率的对比
由图8结合图5可以看出:虽然黄河流域2021—2050年期间降水预测量将增加,径流深却将减少(在HadGEM2模式下的减少率最高),而未来(2021—2050年)流域下垫面的改变更将加剧该区水资源的紧张(图8(a))。由图8(b)可以看出,松花江流域上随着未来(2021—2050年)降水量的增加,径流深也将增加(在HadGEM2模式下的增加率最高),同时,下垫面的改变更将造成该区未来水资源量的增加,在对该区进行未来水资源规划时,应防止该区发生洪涝灾害。图8(c)显示出,在珠江流域上除了GFDL 模式下预测的径流在2021—2050年期间呈增加趋势外,其他3 个气候模式预测的未来径流深均将减少(在BCCCSM1模式下的减少率最大)。同时,从图8(c)也可看出,流域下垫面对该区水资源的影响不大。
4 结语
本研究构建了基于Budyko方程的动态水量平衡模型,选用CMIP5中的4种气候模式(BCCCSM1-1M、GFDL-ESM2M、HadGEM2-ES 和MIROC-ESMCHEM)、3种不同的辐射强迫和大气排放标准(RCP2.6、RCP4.5和RCP8.5),对我国3个代表不同气候区的典型流域(黄河流域、松花江流域和珠江流域)的未来径流进行预测,得到结论如下:
1)3个流域的最低气温均呈显著上升趋势,黄河流域与松花江流域最高气温呈显著上升趋势,珠江流域的潜在蒸发量下降趋势显著(通过T参数检验90%置信区间);除了黄河流域的滑动平均值序列呈显著增加趋势外,松花江流域和珠江流域的区域Budyko方程参数呈现非显著性的减小趋势。
2)预测黄河流域2021—2050年间降水量、潜在蒸发量增加,Budyko方程参数增大,径流深减小;松花江流域未来降水量、潜在蒸发量增加,Budyko方程参数减小,径流深也增加;珠江流域未来在RCP4.5和RCP8.5情景下仅在GFDL模式下的径流深增加,其余3个气候模式预测的径流深减少。
3)与基于不变的Budyko模型参数预测的径流深相比,黄河流域由于未来下垫面改变会加剧该区水资源量减少,松花江流域下垫面的改变更将造成该区未来水资源量的增加,珠江流域上下垫面改变对Budyko模型预测该区2021—2050年间的径流深改变不明显。
