单跳运动员竞技能力结构模型的构建及应用

谢 钧, 王乐军, 龚铭新, 王钰婷, 邹凝祥, 邵企能, 卢天凤

(1.上海体操运动中心,上海 202162; 2.同济大学,上海 200092; 3.上海体育科学研究所,上海 200030)

在我国,技巧运动从 1956年起成为一项独立的体育竞赛项目。1979年,国际技巧联合会吸收中国技巧协会为其正式成员。技巧单跳是观赏性较强、技术含量高、难度大的项目,属于技巧类表现难美性运动项目,对运动员的心理素质、空间感觉、力量、柔韧、灵敏、协调和节奏感等诸多能力素质都有非常高的要求。运动员必须进行专门化的训练，才能掌握复杂的单跳技术和具备适应该项目的身体素质[1]。因此,只有通过科学合理的运动训练,运动员才能培养出良好的单跳竞技能力,进而取得优异的成绩。

竞技能力指运动员的参赛能力,由具有不同表现形式和作用的体能、技能、战术能力、运动智能和心理能力所构成,并综合地表现于专项竞技过程中[2]。竞技能力是运动员比赛成绩的最重要决定因素。运动员竞技能力不同要素之间存在着非常复杂的联系,且各组成要素普遍存在发展不均衡等问题[2-5],因此,构建不同项目个体化的竞技能力结构模型,对指导运动员进行针对性训练意义重大。

查阅国内外文献资料,尚未发现对单跳项目运动员竞技能力结构进行评价的相关报道。依据上海体操运动中心单跳项目跟队实践及与部分省市单跳教练员、运动员的交流发现,目前国家队和各省市单跳队在运动员竞技能力结构评价方面缺乏科学有效的方法,单跳训练仍采用以成套动作练习为主的较为单一的训练模式,未能针对单跳运动员竞技能力结构的具体特点进行个性化和针对性的训练。已有研究人员基于人工智能建模方法对射击[6]、网球[7]项目运动员的竞技能力结构进行了探索应用,取得了较好的效果。

本文拟对单跳运动员竞技能力结构进行分析,通过构建基于人工智能的单跳运动员竞技能力结构评价模型,对单跳运动员的竞技能力结构进行个性化的评价与分析,并给出针对性的训练方法,对运动员赛前状态调整、运动员选材等都具有重要的指导意义。

1 研究对象与方法

1.1 研究对象

以上海市一线和二线单跳运动员吴毓彪、高华帅、吴泽峰、王劲凯、吕沁霖、王瑄、陈泓静等为研究对象。

1.2 研究方法

1.2.1 专家访谈法

对上海市单跳项目教练员、上海体育科学研究所科研人员、上海体育学院和同济大学等高校运动训练专家进行访谈,获取单跳运动员竞技能力评价初选指标体系。

1.2.2 测验法

采用测验法对上海市单跳运动员的身体形态、身体素质、专项体能、专项技术、心理素质等能力指标进行测试,获取相关测试结果。

1.2.3 数理统计法

采用因子分析法对初选指标进行筛选,因子提取方法选择主成分法,因子提取标准为:特征值>1。基于因子分析中各指标在各公因子上的载荷值,确定各公因子代表性指标,最终完成对初选指标的筛选。采用线性回归分析法对相关变量间的数量关系进行分析。

1.2.4 人工神经网络建模法

在确定单跳运动员竞技能力评价指标体系的基础上,以评价指标为输入量、运动总成绩为输出量,构建不同中间层神经元节点数的人工神经网络模型,并以日常训练中所测试的样本数据为训练样本,对所构建的人工神经网络模型进行学习与训练,以此确定模型中不同节点之间的非线性函数关系。每次学习训练完成后,对不同模型的计算值与实际值进行对比,以预测精度最高的模型作为最终建立的最优模型。

本研究采用的神经网络为Elman人工神经网络,由3层组成,分别为输入层、隐层和输出层。除普通的隐层外,Elman神经网络还有一个特别的隐层,称为状态层,该层从普通隐层接收反馈信号。

以单跳运动员各竞技能力指标测试值作为人工神经网络的输入值,以运动成绩作为人工神经网络的输出值。以上海市单跳运动员的比赛和训练数据作为学习样本进行训练,以另外5组数据作为预测样本输入到已经训练过的Elman神经网络中完成识别,并将输出结果与样本实际值进行比较。

采用动态反向传播学习算法,即梯度下降法对网络进行训练,目标是通过对网络各层权值的调节,使样本输出与辨识输出的均方差达到最小。

2 结果与分析

2.1 单跳运动员竞技能力结构初选指标

从单跳项目对人体运动能力的要求出发,在查阅大量国内外文献的基础上,通过与上海市单跳教练员、运动员访谈,制定单跳运动员竞技能力评价初选指标体系,其一级指标包括身体形态、身体素质、专项技术、心理素质4个方面。在一级指标基础上,分别列出二级指标,如表1所示。

表1 单跳运动员竞技能力评价初选指标

2.2 单跳运动员竞技能力结构指标体系构建

对上海体操运动管理中心7名单跳运动员的上述指标进行测试,获得各指标数值。测试共进行2次,2次时间间隔5个月以上。分别对测试运动员的身体形态、身体素质和专项技术初选指标进行因子分析。各因子的纳入标准为:特征根>1。

统计显示,单跳运动员身体形态测试指标可分为身体长度围度因子和身材比例因子。其中,身体长度围度因子的代表性指标为体重,其他指标包括身高、BMI、腿长。身材比例因子的代表性指标为腿长身高比。

统计显示,单跳运动员身体素质测试指标因子包括爆发力因子、力量因子和灵敏柔韧因子。爆发力因子的代表性指标为立定跳远,此外还包括纵跳高度、立卧撑、30 m跑3个指标。力量因子包括30 s背肌测验、负重起踵次数和最大负重起踵重量3个指标,代表性指标为30 s背肌测验和负重起踵次数。灵敏柔韧因子包括坐位体前屈和30 s仰卧两头起2个指标,代表性指标为坐位体前屈。

统计可知,单跳运动员专项技术测试指标因子包括动作高度因子、动作速度因子、专项技术因子、技术稳定性因子。动作高度因子包括原地空翻拔高、10次小翻的重心高度、5次快速空翻的重心高度3个指标,代表性指标为原地空翻拔高。动作速度因子包括离地速度、落地速度、10次小翻的连接时间、5次快速空翻的连接时间,代表性指标为离地速度。专项技术因子包括离地角度和落地角度2个指标,代表性指标为离地角度。技术稳定性因子包括5次快速空翻的水平高度波动和10次小翻的高度波动,代表性指标为5次快速空翻的水平高度波动。

经过因子分析,获得单跳运动员竞技能力评价指标体系(表2),以及单跳运动员竞技能力评价指标测试数值(表3)。

表2 因子分析后获得的单跳运动员竞技能力评价指标体系

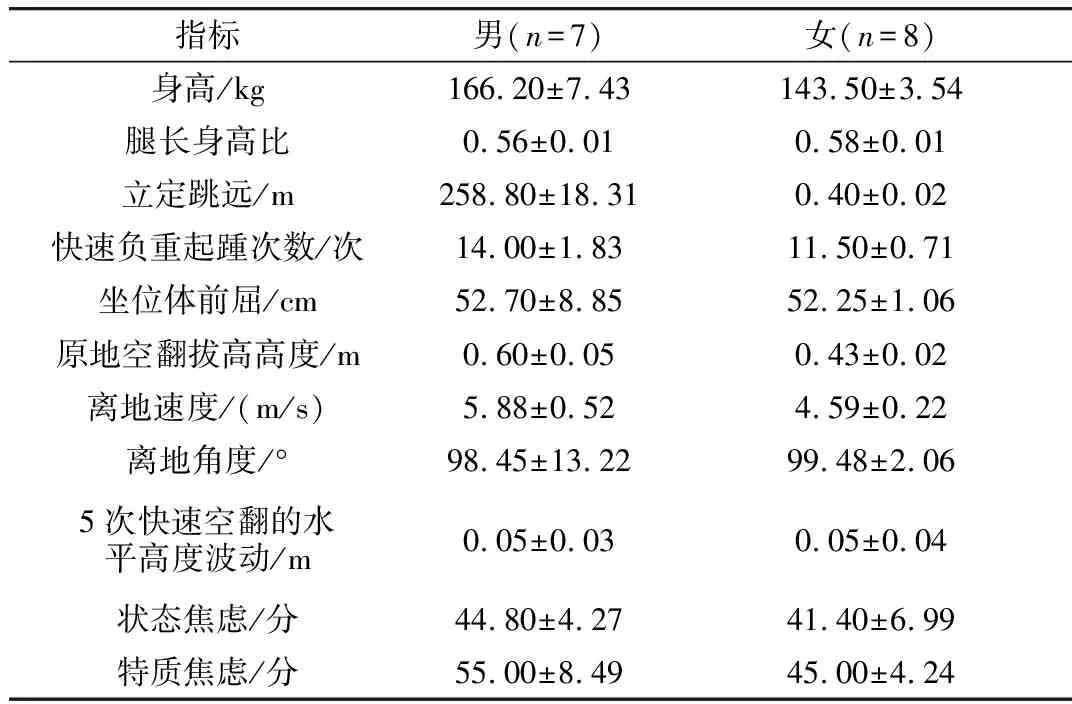
表3 男女单跳运动员竞技能力评价指标测试结果

2.3 单跳运动员竞技能力结构评价模型

2.3.1 线性回归模型建模及评价

在确定单跳运动员竞技能力结构指标体系的基础上,以竞技能力结构各指标为自变量、总分为因变量进行逐步回归分析,获得各指标系数如表4所示。

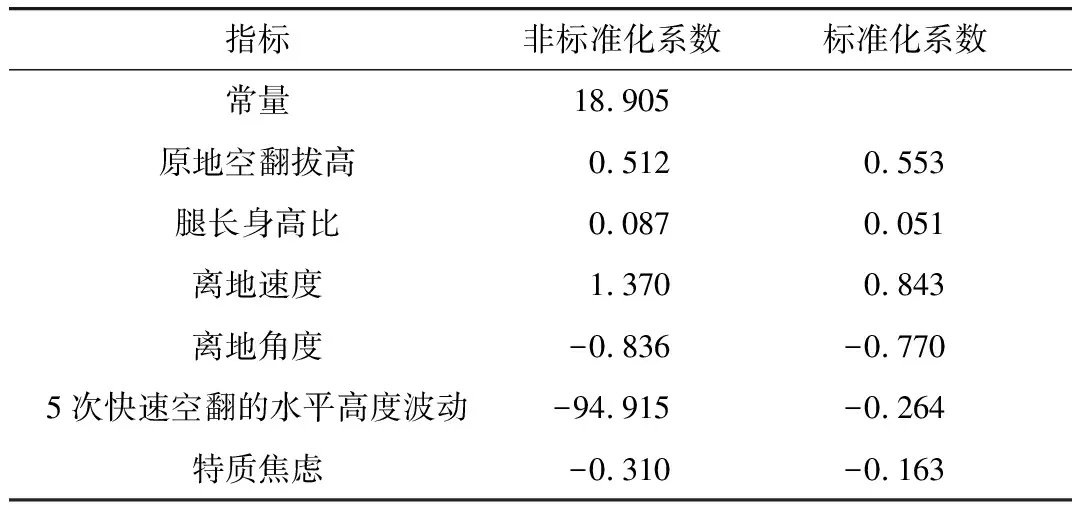
表4 基于线性回归分析的各指标系数

最终确立的线性逐步回归模型为:运动成绩=0.512×原地空翻拔高+0.087×腿长身高比+1.370×离地速度-0.836×离地角度-94.915×5次快速高度波动-0.310×特质焦虑+18.905。

因标准化回归系数为各指标原始数据标准化后建立的方程,其系数的绝对值反映该指标对因变量影响的大小。因此,从标准化回归系数看,对成绩影响最大的是离地速度,其次为离地角度和原地空翻拔高。此外,5次快速空翻的水平高度波动、特质焦虑等对成绩的影响也非常显著。

为检验所构建模型的预测精度,以上海市单跳运动员日常训练和比赛中的数据作为样本,计算上述竞技能力结构指标,并带入模型进行计算,并将预测值与实际值进行比较,发现模型预测精度保持在85.74%～95.56%。

2.3.2 人工神经网络模型建模及评价结果

人工神经网络的建模过程可以描述为:(1)确定模型输入量和输出量;(2)将所有数据进行归一化处理;(3)对人工神经网络模型参数进行设置;(4)对神经网络模型进行训练,在训练过程中根据正确结果对模型参数进行动态调整,待模型预测结果随训练样本数的增加而收敛至一定程度时结束训练;(5)采用所获取模型对结果进行预测及检验。

从人工神经网络模型的特征、本文数据的具体特点及样本数量等,结合前期研究基础,最终选择前向型Elman神经网络作为本课题的神经网络建模模型。

Elman神经网络具有与前向网络相似的多层结构，其主要结构是前馈连接,包括输入层、 隐含层、 输出层,其连接权可以进行学习修正。反馈连接由一组“结构” 单元构成,用来记忆前一时刻的输出值,其连接权值是固定的。在这种网络中,除了普通的隐含层外,还有一个特别的隐含层,称为关联层 (或联系单元层 )。该层从隐含层接收反馈信号,每个隐含层节点都有一个与之对应的关联层节点连接。关联层的作用是通过连接将上一个时刻的隐层状态连同当前时刻的网络输入一起作为隐层的输入,相当于状态反馈。隐层的传递函数仍为某种非线性函数,一般为 Sigmoid函数,输出层为线性函数,关联层也为线性函数。

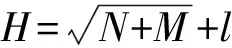
为了避免在神经网络的计算机模拟过程中数值发生溢出,必须对网络输入层和输出层的各单元值进行标准化处理,并使它们处于区间[0,1]或[- 1,1]中。本文采用的输入参数的标准化方法为:

式中,xmax为该组变量的最大值,xmin为该组变量的最小值。

经过网络优化过程后,Elman网络隐藏和关联层节点的个数为9,最终建立的最佳网络模型如表5所示。

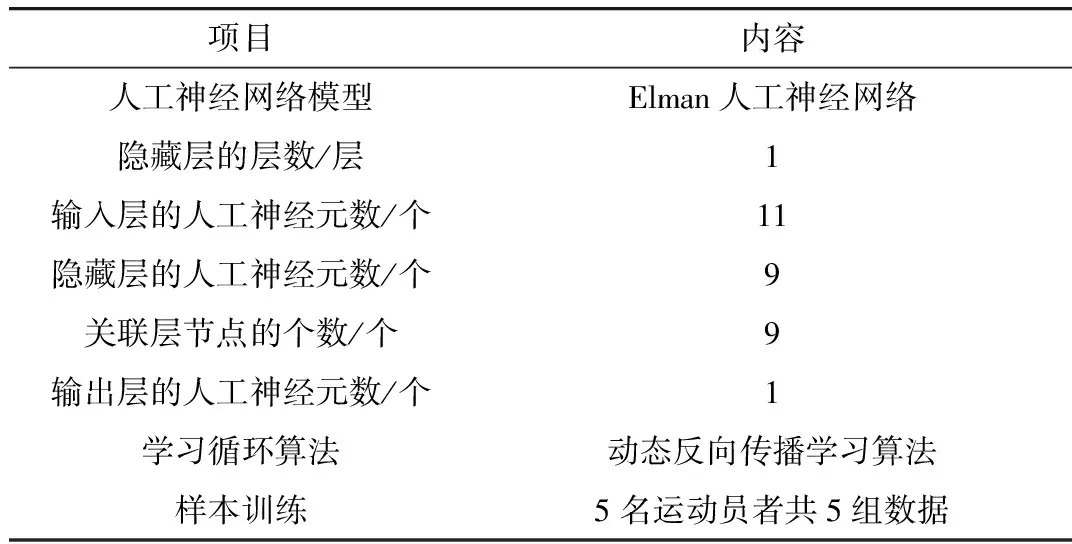
表5 人工神经网络模型参数一览

为检验所构建模型的预测精度,以上海市单跳运动员日常训练和比赛中的数据作为样本,将上述竞技能力结构的11个指标数据带入模型进行计算,将预测值与实际值进行比较,得出模型预测精度保持在90.71%～97.19%。

2.3.3 神经网络模型与线性回归模型的估计精度对比

为比较人工神经网络模型与线性回归模型在预测精度方面的差异性,以上海市单跳运动员日常训练和比赛中5组预测样本数据为依据,计算预测值与时间值的相关系数、平均预测精度、最大预测精度、最小预测精度等指标。发现:人工神经网络模型预测值与实际值的相关系数为0.925,具有显著的相关关系。线性回归模型的预测值和实际值的相关系数为0.666,不具有非常显著的相关关系。在预测精度方面,人工神经网络模型也表现出优于线性回归模型的优势,其预测精度在90.71%～97.19%,平均预测精度高达94.00%;而线性回归模型的预测精度在85.74%～95.56%,平均预测精度为89.56%。

2.3.4 单跳运动员竞技能力结构评价模型的应用

运用所构建的单跳运动员竞技能力结构评价模型,对上海市单跳运动员的竞技能力结构指标进行测试,并将测试数据输入竞技能力结构评价模型,对单跳运动员的总体竞技能力进行评价，并预测运动员特定竞技能力提升对成绩的影响,为运动员竞技能力的发展和科学化训练提供指导意见,取得了较好的应用效果。

3 小结

构建单跳运动员竞技能力结构指标体系,建立基于人工神经网络的单跳运动员竞技能力结构评价模型,测试发现模型具有较好的预测精度。在诸多竞技能力指标中,对单跳运动员成绩影响最大的是离地速度,其次为离地角度和原地空翻拔高。此外,5次快速高度波动、特质焦虑等对成绩的影响也非常显著。训练中可应用人工神经网络对运动员的竞技能力结构进行评价,动态获知竞技能力结构改变对运动成绩的影响,为单跳运动员竞技能力结构的综合评价和针对性训练提供科学性的指导意见。